AtCoder Grand Contest 029 will be held on Saturday (time). The writer is yutaka1999. This contest counts for GP30 scores.
Contest duration: TBD (around 2 hours)
The point values will be announced later.
Let's discuss problems after the contest.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
AtCoder Grand Contest 029 will be held on Saturday (time). The writer is yutaka1999. This contest counts for GP30 scores.
Contest duration: TBD (around 2 hours)
The point values will be announced later.
Let's discuss problems after the contest.
| Name |
|---|



Sorry for the delay of editorial translation. Meanwhile, some hints for E/F:
Let Sr be the set of rooms we visit before we reach room 1, in case we start from room r.
Consider room 1 as the root of the tree.
Let x be an arbitrary room, and let p be its parent.
We can show that Sx is a superset of Sp.
How can we characterize rooms that are contained in Sx but not in Sp?
Let's choose one vertex from each set, such that no vertex is chosen multiple times.
If we can't do this, the answer is "no".
Thus, without loss of generality, we can assume that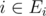 for each i.
for each i.
By the way, if for some tuple of indices (i1, ..., ik), the size of the union is at most k, we can show that the answer is "no".
is at most k, we can show that the answer is "no".
How to find such a tuple in case such a tuple exist?
How to construct a valid tree in case such a tuple doesn't exist?
This round had really bad scoring. D was easier than A, but for some reason costs more than C or D. And F was not harder than E but costs almost two times more.
It's hard to estimate the difficulty and we thought F is very hard. But judging from the number of ACs, I think the order of problems was correct (may be C/D can have the same score).
There is always a bias in number of accepted solutions towards earlier problems, because some retards like me don't read the next problem until they solved the current one.
"D was easier than A" — how do you want to be treated seriously when you're saying things like this?
A required at least some ideas, while D is just simulating the process until we bump into an obstacle. What's so hard about that?
I think you don't remember what A asked for. D required a simulation provided you found out the strategies. I also found it easier than B and C, but that's because my solution to B is overovercomplicated and for some reason I simply couldn't think about C. However, saying shit like D was easier than A is the definition of an exaggeration.
What strategy? That the first guy should always go down? Yes, that's very hard.
Wow. Didn't get it during the contest :(
Ok, so saying in your language, what idea in A are you talking about?
That we need to count the number of inversions.
I've just calculated for each
Bthe number ofW-s it will be swapped with. I didn't realize that this is the same as calculating inversions, however it's obvious, of course.Calculating the number of inversions in a binary word is, again, much easier than calculating the number of inversions in general.
Do you really find this observation with inversions harder than coming up with the solution for D? I mean, as for me, one can come up with a solution for A more instantly after reading the statement than for D. And it's without implementing.
TL;DR: yes, that [number of inversions equivalence] is very hard.
Yes, of course I didn't write general algorithm for inversions, I did it the same way as you. And I didn't say that it's hard. But I can understand that for someone it may not be obvious. What I can't understand is how someone can try to solve D and fail. I have no idea how this can happen. Like what way of thinking you must choose to not come up with a solution? Seeing people like qwerty787788 and Swistakk not solving it blows my mind. It's like seeing red coder failing to solve A+B. I don't want to insult them, and don't think that they are stupid, in fact they are much smarter than me. But I'm honestly very confused right now.
I pretty much solved it, but forgot "-1" in one place and abandoned this problem xD. AC in upsolving short time after end of contest.
Maybe that's not something mind blowing, but maybe I will regain 10% of respect I lost by taking this 447th place xD.
D was harder than A because of the implementation and because of the ("extremely tough") observation that if the first guy will stop then the games ends. Also because it was scored with 800 it was confusing how could a solution so obvious be right.
Yes, I agree that it was harder to implement than A, I didn't take this into consideration. But your argument about scoring is exactly the reason of my complaint: that it should not have score of 800 and it definitely should not have more points than B and C(I hope we can agree at least on that).
Yes we can ;)
To join the downvote party, I also think A was harder than D, and don't know why D was proposed at all.
I could solve A fast, as the inversion invariant idea was well known. However, D was simply translating the problem statement into code, with the idea being... umm.. that Takahashi can't stop?
Even B and C was not that easy for me, so it was pretty clear that something is wrong with my understanding. but I really couldn't found my misinterpretation, so I wrote down the code in worry and got an uncanny AC.
Btw, I enjoyed all other problems very much. Thanks for problemsetter!
I agree that D is a little bit silly once you see what the problem is talking about, but clearly not everyone was thinking in the same way as you, or there would be more solves...
(For example, if you consider dp[x][y] of how many more moves starting from position x, y, then you won't really get to this solution...)
However, problem A is probably one of the most (if not the most) textbook and straightforward problems to ever appear on an AGC, I don't see how its difficulty can be compared with any other problem with any content at all.
To be frank, A took me something like 1 minute to came up with solution (what I mean is that 1 minute is rather long, not rather short :D), so I can explain you why it was not obvious to me. Statement was talking about some token with two colored sides and operation described was flipping colors of two neighbouring tokens. In this way it was completely not clear to me how to solve this problem and if it wasn't for its point value I would think it is at least a bit challenging problem cause I didn't see any good way of grasping that concept of changing colors. However then I observed that instead of thinking of two tokens staying in their place but changing their colors I observed that it can be thought of as two tokens with different colors keeping their colors but swapping their positions. Once stated, it is completely obvious that these two interpretations are equivalent, just a bit different way of putting the same thing in words, however in this second way it was completely obvious for me how to solve it. See the difference and why that matters so much?
Tbh on second thought I think that my thinking process was a bit different. Being clueless, I decided to investigate samples and see some patterns and I just noted that answer is what it is (sum of number of Bs on left over Ws) and realized why it is like that by following that process I described in previous paragraph (which after noting this pattern was so obvious it took me sth like 1 second after being clueless for cosniderably longer time).
Sure, if you go by that measure of difficulty...
Can you really imagine someone in division 1 getting stuck on A though? On the other hand, it's very easy to imagine someone not knowing how to solve D after some time.
My main goal was to illustrate how different way of thinking about basically the same thing may lead to someone coming up or not with a solution, because sometimes someone's problem lies in a different place than we think.
And I surely think that A is easier than D and my first thought to D was designing that dp table as you described (then I noted N<=2e5 and abandoned this idea and quickly came up with right approach). But as I was clueless about A for 1 minute, I can imagine some other participant being stuck on this for much longer because of lacking step "first way of thinking -> second way of thinking", but I can't imagine div1 guy being stuck on step "second way of thinking -> proper solution".
Is the following greedy for problem C correct?
Given that c distinct characters were used in the first i - 1 strings, to find the string Si: find the lexicographically smallest string X composed by at most c distinct characters which is greater than Si - 1. If it exists, make Si = X. Otherwise, find the lexicographically smallest string Y composed by at most c + 1 distinct characters which is greater than Si - 1, make Si = Y and make c = c + 1.
I implemented this initially but i think it's incorrect, consider a case where there are only 2s in input and you run your greedy which generates sequence, "aa", "ab", "ba", "bb", "bc" .. if you observe you missed "ac" because at the time of generating 3rd string, character c was not allowed. So this approach will fail on below test case:
So, i approached this with doing binary search on number of characters allowed and check if that is fine.
How many GP30 points do I get for taking 447th place?
We need to move to GP450 ASAP!
Thanks for the contest!
My screencast with commentary: https://youtu.be/02VV330Avc8
It might be irrelevant, but I'd like to mention that editorial of AGC028 is still uncompleted (for problem F).
UPD: Now it is completed.
So...where can I see the editorial? It's not present in the Atcoder contest front page.
The English editorial is ready now.