Hello,
Greetings good people of Codeforces. I cordially invite you all to take part in the online mirror of 2018-2019 ACM-ICPC, Asia Dhaka Regional Contest. The contest will be held on Saturday, January 19, 2019 at 16:00 (UTC+6).
The onsite contest took place on Saturday, November 10, 2018, where 300 teams competed for a spot in the 2019 ACM ICPC World Finals. I know its been a while, but hey its better late than never.
Contest duration will be 5 hours and will follow standard ICPC rules. The problem set consists of 10 problems and was prepared and tested by Jami_CSEDU, shovonshovo, sgtlaugh, dragoon, nfssdq, raihatneloy, sn23581, SnapDragon, Shahriar Manzoor, Monirul Hasan, Imran Bin Azad and Mehdi Rahman. Moreover, special thanks to Rujia Liu for reviewing and also forthright48 and ridowan007.
Note to any one who participated in the onsite contest, please refrain from sharing or discussing the problems here before the contest. The analysis will be posted once the online mirror ends and afterwards we can all discuss about the problems here.
I hope you enjoy the contest. Cheers!
UPD: BUMP! 24 hours to go, buckle up!
UPD: Contest has started, see you in the arena.
Editorial: https://docs.google.com/document/d/1VEz9q-pXK2KuRJh2WwtlhmdQ882nFDMCdi-7ZOxE47w/edit?usp=sharing











Auto comment: topic has been updated by sgtlaugh (previous revision, new revision, compare).
How to solve A, C, G and I?
Please check the editorial and let me know if you have further questions.
for the problem I, I did as below but I didn't get AC:
We can find the shortest distance of a point in 3D space to a triangle in O(1). at least one of endpoints of the shortest segment that connects two triangles is on edge of one of the triangles (?), then I guess, we can use ternary search to find that point on each of 6 segments.
does it right?
btw, how to solve H and F?
My solution for H: I guessed that the transition is formed by keep rotating clockwise/counterclockwise, which is equivalent. So you can just implement one rotation, the change of positions of # form some cycles, take the least common mulitple of all lengths of the cycles will yield the answer. To compute the LCM, one can just record the power for all primes less than 40000.
That's correct. This problem looks daunting at first glance, but ultimately boils down to finding the LCM of all cycle lengths.
However it remained unsolved in the onsite contest: https://algo.codemarshal.org/contests/icpc-dhaka-18/standings
My solution for F: one observation is that the intersection of two paths is also a path. Let's say the two paths are (u, v) and (uu, vv), then the intersection of the two paths(if they intersect) is the path between the vertices of the four that have largest depth: lca(u, uu), lca(u, vv), lca(v, uu) and lca(v, vv).
For I, you can solve it in that way. Although ternary search is not the intended solution here, so you might need some optimizations depending on your implementation. The intended solution has O(1) complexity.
For F, you can simply use bitset. For each node, keep a bitset called path containing the set of nodes from that node to the root. To find the bitset of any path from nodes a-b, we can now do (path[a] or path[b]) xor path[lca(a, b)], and set lca(a, b) explicitly
sgtlaugh bhaiya, shouldn't it be (path[a] or path[b]) xor path[parent[lca(a, b)]] ?
Yeah sure, but I left out that part intentionally since the parent may not always exist (if the lca is root). Updated the comment, should be clearer now.
Can you explain, how F will not give TLE?
You mean the bitset approach?
The overall complexity for the bitset approach will be O(N^2/32) + O(Q*N/32) per test case. There can be at most 50 cases, and N and Q can be at most 10,000. So even in the very worst case, you don't need to do more than ((10000^2/32) + (10000*10000/32)) * 50 operations, which is roughly 3*10^8.
This should run well under 1 second since the operations are very simple. And the time limit is 3 seconds so that should be more than enough.
Can I get all the test cases for problem E?
No you cannot.
However, this is the case for which your latest code fails.
Input:
Correct output:
Problem I is a well known 3D geometry exercise, which I like cause it have beautiful solution. I'd like to use this opportunity to write some more detailed solution. Checking out this problem will be also helpful.
If both points strictly lies inside of triangle, you can always move toward a direction with non-increasing distance. Now, one of them is in triangle, and one of them is in line segment.
If one point strictly lies inside of triangle, and one point is not an endpoint of line segment, you can again find a good direction. Now, you should calculate 6 point-triangle distance, and 9 segment-segment distance.
Point-triangle distance could be easily checked. If it's orthogonal projection lies in a triangle, you can just calculate the distance between plane and point. Otherwise, it's a point-line distance which is also easy. Then, what about segment-segment distance?
Now we should calculate the distance between segment and segment, which is the meat of the problem.
First idea is to parametrize the segment and do nested ternary search, which is actually OK as TLs are lenient and you don't need exact numbers. But it's boring.
Second idea is to parametrize the segment and calculate partial derivative by hand, which is O(1) and gives an exact number. But it's boring and disgusting.
Having a nice geometrical model like Step 2 is desirable, but how? Hint: Parametrization actually helps.
Let the endpoint of both segment be (S1, E1) and (S2, E2). What you actually want is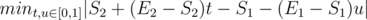
Plot all areas with coordinate X + Yt + Zu. How does it look like? A parallelogram, which is a union of two triangles. Then, you should calculate the minimum distance between (0, 0) and two triangles, which is what we exactly did in Step 2.
Can I get the test case for F. My approach is similar to what Roundgod mentioned here, but I am not able to figure out what's wrong in my code.
Sure you can, send me your email via DM and I'll share the package. You should be able to see the cases from coach mode in gym too.
Thanks.
Can someone explain how to solve B. I read the editorial but I am not clearly getting what would be the formula for counting the number of inversions.
I think that my solution is a bit differ from solution in the editorial but I'll try to explain how I compute number of inversions.
We are solving problem in range $$$[1, ..., R]$$$. Let's split this range into $$$O(10*log_{10}R)$$$ smaller ranges. Let's fix the prefix of this number and the following digit. Then we have a choise for the last $$$k$$$ digits and the amount of numbers in this range is $$$10^k$$$. For example, if $$$R = 2643$$$ and we fixed one digit and set the next one to 4, we have a range $$$[2400, ..., 2499]$$$. Let's split inversions in following 3 types:
1) Inversions on a prefix. We can compute them by hand and multiply by $$$10^k$$$ — for each number in the range. In our case we have one inversion on a prefix and it appears in 100 numbers.
2) First digit of inversion is on prefix, but second isn't. Then, let's fix this digit on prefix (its position). If the digit we fixed is $$$a$$$, we have $$$9 - a$$$ digits that are more than $$$a$$$. In $$$10^k$$$ numbers from $$$[0, ..., 10^k - 1]$$$ (with leading zeroes) each of this digits appear with probability $$$\frac{9 - a}{10}$$$ on each of $$$k$$$ positions — on each position independently. So, there are $$$(9 - a) * 10^{k - 1} * k$$$ inversions with digit $$$a$$$. In range $$$[2400, ..., 2499]$$$ there will be $$$5 * 10 * 2$$$ inversions with $$$a = 4$$$ and $$$7 * 10 * 2$$$ inversions with $$$a = 2$$$.
3) Both digits of inversion aren't on prefix. Amount of them is the same as amount of invertions in $$$[0, ..., 10^k - 1]$$$ (each number with leading zeroes). We can precompute this number for each $$$0 \leq k \leq 14$$$ by fixing the first digit and using already computed values.
After this, we have to check numbers with $$$number$$$ $$$of$$$ $$$digits$$$ $$$<$$$ $$$number$$$ $$$of$$$ $$$digits$$$ $$$in$$$ $$$R$$$. This values can be precomputed, too.
My submission. I hope that it helped you.
This is actually more intuitive and clear. Thanks a lot.
Nice! We can solve the problem with standard digit DP as well. To calculate the value any particular digit adds to the inversion, we only need to know how many digits greater than it were placed before. As such we can have the frequency of each digits as a state in DP (this number won't be very large) and apply standard digit DP as usual.
Solution
I thought of this but we have a lot of queries also. The sum of frequencies won't exceed 14, but isn't it still very high? How were you able to calculate the total number of states?
Isn't that just the stars and bars problem for a fixed length $$$N$$$ with $$$D$$$ (here $$$D=10$$$) digits to choose from? For $$$N=14,$$$ there are $$${14 + 10 - 1}\choose{10}$$$ or $$$1144066$$$ unique states.
https://oeis.org/A001287
And you can apply memoization for multiple queries. You don't need to compute the whole thing over and over again, but just for each prefix. It's a fairly common trick in digit DP problems.
Can anyone explain solution to Problem G. I read the editorial but couldn't understand how the type 3 queries can be solved using centroid decomposition and segment tree..
I don't use mentioned in editorial lca technique in my solution.
First, we convert each type 3 query into $$$M$$$ queries (we skip companies that have 0 shops now):
Given vertex $$$V$$$ in a tree and a range $$$[L_i, ..., R_i]$$$. Find the distance from $$$V$$$ to the nearest vertex from this range.
In this case we need to calculate distance between $$$V$$$ and $$$L$$$. Let's do it in the following way:
Define $$$Level_U$$$ as the depth of vertex $$$U$$$ in the centroid decomposition tree. It is well known, that on each path $$$XY$$$ there is exactly one vertex with the minimum level. Define $$$Parent_U$$$ as the parent of $$$U$$$ in the centoid decomposition tree.
Define $$$T_X$$$ subtree of given tree that contains $$$X$$$ and consists of such vertixes $$$Y$$$ that $$$Level_X$$$ is the minimum level on path $$$XY$$$ ($$$X$$$ will be the root of such tree). From the previous fact we know that trees of vertixes of the same level don't intersect and vertex with level = $$$l$$$ is in $$$O(l)$$$ trees.
From the construction of Centroid Decomposition we know that there are at most $$$O(logN)$$$ levels.
Let's create array $$$dist[LG][N]$$$ where $$$dist[j][v]$$$ is the distance from $$$v$$$ to such $$$u$$$ that $$$Level_u = j$$$ and $$$v \in T_u$$$.
How to answer the query now? Let's check all the possibilities for the vertex with the minimum level. It should be on the path from $$$V$$$ to the root of the centroid decomposition tree. If we fix it and it's level is $$$j$$$ then we update answer with $$$dist[j][L] + dist[j][V]$$$.
What is the problem we have now? Let's look at the numbers $$$dist[j][L], dist[j][L + 1], ..., dist[j][x], ..., dist[j][R]$$$. We should update our answer using only some of them — $$$x$$$ must be in the same level $$$j$$$ tree as $$$V$$$.
Let's replace that table with the following table: $$$dist[v][u]$$$ is the distance between vertices $$$v$$$ and $$$u$$$ if $$$u \in T_v$$$ and $$$INF$$$ otherwise. This table takes $$$O(N^2)$$$ memory but only $$$O(N*logN)$$$ values are meaningful. Let's compress all rows of this table. Then we have $$$O(N)$$$ arrays and we can build a segment tree on each of them.
We can don't care about moving L and R in questions to the segment trees as I did in This submission. Hope this comment will help you.