den2204's blog

Codeforces Round #532 (Div. 2) — Editorial
By den2204, history, 6 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +69
  • Vote: I do not like it

Comments Comments (70)
| Write comment?
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Auto comment: topic has been translated by den2204 (original revision, translated revision, compare)

→ Reply
»
6 years ago, # |
  Vote: I like it -111 Vote: I do not like it

this wouldn't have been needed if you gave us actually useful good problems.

→ Reply
»
6 years ago, # |
  Vote: I like it -31 Vote: I do not like it

why so short solution for D , please elabprate what u r saying den2204

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +12 Vote: I do not like it

    For D,

    Let us solve this question assuming that the king is at the centre of the board at (500, 500). (If it is not at the centre, then we need around at max 499 steps to reach it as it could have been at the corner.)

    Once you are at the centre, consider the four newly created divisions (or quadrants) of the board. Choose the 3 divisions which do not have the minimum number of rooks. By doing this you ensure that the combination of these 3 divisions has atleast 666 * 3/4 >= 499 rooks otherwise you have not chosen the top 3 divisions correctly (basic pigeon hole principle).

    From now, just move the king away from the section with the minimum rooks ( < 499 in any case) along the diagonal (this ensures that rows and cols are handled together).

    Keep doing this till the corner. You are bound to get a check by a rook as no. of steps required to reach corner from the centre is 499 and from php we know that there are atleast 499 rooks there.

    Eg. 1. king at 999,999

    1. move king to 500,500

    2. let quadrant IV have minimum rooks (167). So quads I, II, III have 499 rooks combined.

    3. while going towards 0,0 (top left point inside quad II), we will end up checking from rows 500 to 1 and cols 500 to 1 simultaneously while going towards the top left diagonal.

    4. since no. of steps to reach the diagonal is at max 499 and we know that there are 499 rooks in these 3 quads, we will get a check(mate) for sure.

    NOTE: I may be off with the numbers by 1 or 2..but i hope you get the point. All of this will occur in less than 1000 steps

    A good question it sure is.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +3 Vote: I do not like it

      There is one corner case you need to handle, which is if rooks are on the king's diagonals. You will need to go the nearest row and col together to eliminate the rook as you cannot eat it. I'll fix and share a code with good comments soon

      → Reply
»
6 years ago, # |
  Vote: I like it +56 Vote: I do not like it

F can be solved in O((n + q)logC).

Code: https://codeforces.net/contest/1100/submission/48345032

System tests for D are too weak. My submission that moves king to the center and then allways moves it to the same corner passed system test.

Code: https://codeforces.net/contest/1100/submission/48362464

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you shortly explain your solution for F?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +25 Vote: I do not like it

      It's very similar to the standard Gaussian elimination with xors. The difference is that when adding new element to the structure, if we already have an element with the same highest bit, then we keep one with the highest index in the array and continue the process with the other.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Actually you can serve queries online if you precompute and store the linear basis for each position.

    → Reply
»
6 years ago, # |
← Rev. 8   Vote: I like it +48 Vote: I do not like it

Good Explanation for C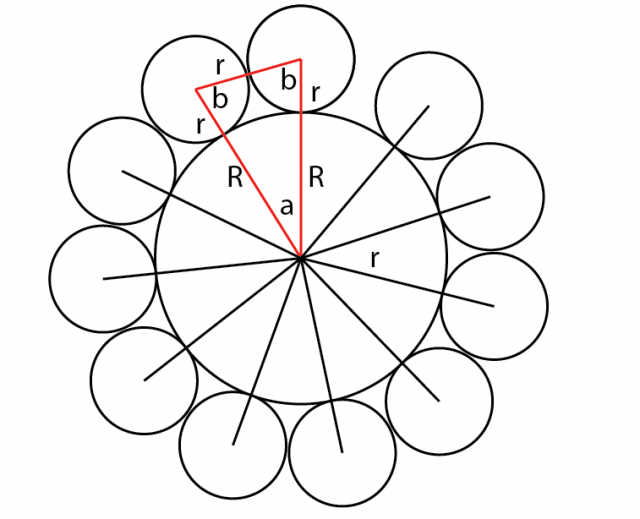 Captu2re

the Radius of the innar circle = R and radius of the outer circle = r by connect the center point of the innar circle with two center points of the other consective small circles , the angle (a) = 360 / n and the traingle is Isosceles triangle from the cousine law we will reach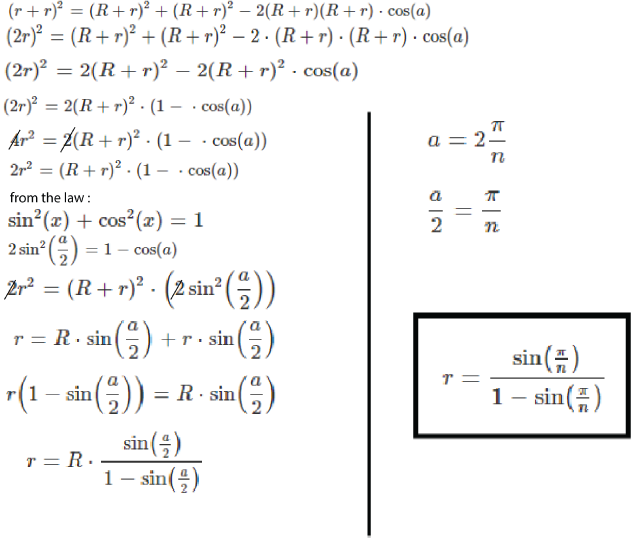 Untitled-1

#include "bits/stdc++.h"
using namespace std;
const long double PI = acos(-1);
int main()
{
  int n , R;
  cin>>n>>R;
  cout<<fixed<<setprecision(7)<<sin(PI / n) / (1 &mdash; sin(PI / n));
}
→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Nice explanation. One could also note that the polygon formed by connecting the centers of adjacent outer circles is a regular n-gon inscribed in a circle of radius R + r.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      thank's bro . great observation

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But , how would you deduce the value of 'r' (or the radius of the outer circle) from that sir ???. I couldn't get your point

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        From basic geometry we know that side length of a regular n-gon with circumradius R' is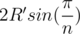 . In our case we observe that the side length of our polygon is 2r (r is unknown) and that the circumradius is R + r. Therefore, we get that 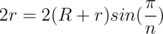and solve for r.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +3 Vote: I do not like it

          That's really awesome sir !!! Thanks a lot !

          → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Another approach is to note that if you cut the triangle in your diagram in half (bisect the angle a) you have a right angle triangle where the hypotenuse is the line connecting the centres of the big circle and little circle. This gives .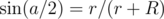

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Thank you very much! This helped me a lot.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    why (r+r)^b ? it's (r+r)^2 and how you get second equation ? i think it will be (2*r)^2 = 2 * (R+r)^2 *(1-cos(a))

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry , it's ^2 not b I has a mistake while typing in the second equation try to take (R + r)^2 as a common factor and you will get (2r)^2 = (R + r)^2 * (1 — cos(a))

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        let say x=(R+r)^2 then: x+x-2*x * cos(a) take x as common factor will be x*(1+1+2*cos(a)) then: x*(2+2*cos(a)) take 2 as common factor from(2+2*cos(a)) it will be x * 2 * (1-cos(a) )

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        for more let R=2 , r=3 , cos(a)=1/2=0.5; the res for first one will be 25 + 25 — 2 * 5 * 5 * 0.5=25 but in you second one will be 25 * 0.5=12.5

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://codeforces.net/contest/1100/submission/48402367

why D is falling? I just can not understand, plz help

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it 
    while(kx!=500&&ky!=500)

    Should be || instead &&.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank!

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I had same problem and used your solution and got AC but can't understand why || works and && doesn't. can you explain?

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -9 Vote: I do not like it

I think, author's solution for D is wrong. For example, put the king to the center, put 333 rooks to positions 1 1, 2 2, 3 3,... 333 333, and other 333 rooks to positions 999 999, 998 998, 997 997,... In such case the king has no chance to win.

I tried to find additional restrictions in the task, excluding such an example, but don't see it. Am I wrong?

UPD: Thank you, guys, you are right

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +17 Vote: I do not like it

    Just head straight to (999, 1) and you'll win.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +9 Vote: I do not like it

    You can move from (500, 500) to (1, 999). It will take you 499 steps while the opponent would have to move 666 rooks

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Could somebody explain the time complexity of the hull method in F please?

I am seeing a O((nlog(n) + q)log2C) time complexity, with the recurrence

T(n) = O(n)log2C + T(n / 2) + T(n / 2)
→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    There are two parts. The first part is answering the queries, and the second part is divide-and-conquer itself. We should see them as seperate parts.

    For the first part, each query costs log2(C), which is the time of combining the left basis and the right basis, so answering the total q queries will cost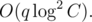

    For the second part, calculating the left basis list and the right basis list both costs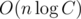 , so the recurrence will be 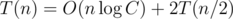. Then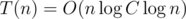

    So totally the complexity will be something like .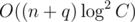

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      The part about the queries don't confuse me. Ignoring the O(logC) components.

      You mentioned that the recurrence is:

      with the solution T(n) = O(nlogn)

      But they have reported the time complexity as O(n).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        I am trying to understand you.

        What do you mean by But they have reported the time complexity as O(n). ?

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Oh, thanks for being so patient.

          In the last line of the editorial they have written:

          Complexity is O((n + q)log2C) or O(nlog2C + q).

          This has an O(n) term, but no O(nlog(n)) term, and that is what I meant by

          But they have reported the time complexity as O(n).`

          I feel that they should have a O(nlogn) term in the complexity.

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            Yes. I think so too.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              den2204 could you take a look at this?

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                6 years ago, # ^ |
                  Vote: I like it +5 Vote: I do not like it

                More strictly, complexity of first solution is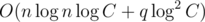 , because we can add vector to hull in time proportional to the size of the basis — .

                → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

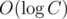An International Grandmater(djq_cpp,He is only 13!!!!) told me there are answer code for problem F on the Internet.I copy the code and get accepted(I didn't take part in the contest.).So F is a problem appeared before.That's really bad!!!Submittion 48412606

→ Reply
»
6 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Problem D 091 there: http://olympiads.win.tue.nl/imo/soviet/RusMath.html

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -26 Vote: I do not like it

(https://codeforces.net/contest/1100/submission/48425126)

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    Seriously dude, it is test case 1. Don't expect other people to help you debug when you haven't put in the effort.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Why first solution fails and second one passes for E?

First solution
Second solution
→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In ques E,i am getting wrong answer on test case 7 but am not able to identify the problem in my code.Can somebody help me with it please?

link : https://codeforces.net/contest/1100/submission/48427349

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain B plz. If possible give your code too xD

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If I return 1 at the end of interaction I will get Runtime Error. Had many RE because of that!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to implement E? Any suggestions? Thanks in advance

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

48427795 Could anyone help me with prob E. My solution is an implementation of the tutorial, however I get a TLE for test case 10. Many thanks in advance.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You don't need to delete/copy edges every iteration of your binary search. You can simply ignore them when you check for cycles.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 4   Vote: I like it 0 Vote: I do not like it

      48453854 Thanks, but I could only move forward till test case 12. Again stuck at TLE. Could you please have a look? Thanks again.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        There are a few things you can improve. Try: removing usage of a HashSet hs (not sure why you need it at all); shuffle array before sorting; you don't need to find a solution in every iteration of your binary search: simply use isCycle in your search and once you found k, you can find which edges to reverse.

        → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

For E, can someone explain what i'm doing wrong.

  1. I binary search on K(max edge wt to be removed) as given in the editorial. Find appropriate K.
  2. To construct graph remove all edges having wt <= K.

code For 3rd tc, K is correct but it contains cycle if i remove edges by above rule.

I did this because here it says reversing an edge is same as removing in directed graph.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    So basically what have you have done wrong is that you are telling the indices of every road whose weight was lower. You only have to print the ones that in fact did get reversed.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Got it, thanks. in fact did get reversed

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But in the question it is specified that we need not to minimize number of roads. So printing all the roads whose weight is less than K should also be true?

      → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain or link me to what is being done with the hulls , and what are hulls ? Is it related to the convex hull or something related to do? Thanks

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    a set of number which is linearly independent in xor? that is,you can make a linear hull using some numbers, and using the numbers in the linear hull, you can get every number which you can get with the original numbers by xor

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E, after finding the min value of k using binary search how to determine which edges to be reversed. For example-

3 3
1 2 10
2 3 10
3 1 10

This will give me the k = 10 but how to determine which edge to remove.I was thinking of removing all the edges with val<=k. But the above test case will pose the problem , that the graph will become disconnected.Help please.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You need to sort the remaining graph topologically, then figure out which edges to flip.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

why the solution 2 for F is O(nlog2C + q)? I think it should be O((n + q)logC) or did I misunderstand it? here is my solution

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I have another way to solve B.

If we list the positions of every difficulty in n lines such as :

1: 3 11
2: 1 4 5 6 8 9
3: 2 7 10
(the first example)

we can easily find that a round will be held when p - th problem is put into the pool, where p is the maximal number in each column. (In the example above, they're 3 and 11.) So we can denote cnt[i] as the number of problems in difficulty i and f[i] as the maximal number in i-th column and then do f[++cnt[a[i]]] = i. Because the position i is increasing, f[j] is the maximal number. Print 1 if any f[j] (j ≤ min(cnt[k])) equals to i, otherwise print 0. The complexity is also O(m).

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Update: I understood the problem incorrectly. I thought that the king must stay checked after a rook moves. Not sure why. So my example is an instantaneous win for the king.

[It seems to me that the proposed solution to D is incorrect. Consider 5x5 board with 3 rooks and the king located like this (X for a blank):

RXXXX
XXXRX
XXKXX
XXXXX
XXXXR

Here we have 3 rooks and the king needs (sort of) 2 steps to reach the corner. However, considering that we can't take the rook at the first step — it is impossible to win. If we go right-up or up-right it is easy to see that all rooks can escape.

Now you can create a configuration on 999x999 board where 500 rooks are placed in 3 quadrants such that this bad case will occur when the king is 2 steps away from the corner (and blocked by the rook). And you can easily place other 497 rooks such they will escape one by one as the king moves diagonally from the field (500, 500).

Did I miss something?]

→ Reply
»
5 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Explanation for 1100C - NN и обман зрения

→ Reply