I am just curious.
Suppose some problem has a randomized solution which fails with probability at most 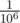 . If it has, say, 100 tests, the probability of failing some of them is about
. If it has, say, 100 tests, the probability of failing some of them is about 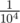 . Therefore, once in 104 it may happen that correct randomized solution doesn't pass.
. Therefore, once in 104 it may happen that correct randomized solution doesn't pass.
Has anyone experienced anything like that? Maybe even the exact solution that didn't pass got AC after submitting it the second time? Or am I getting something wrong?











Something like that happened to me once when upsolving. I had a solution that used random_shuffle and there was an anti-random_shuffle test case. When I replaced random_shuffle with two random_shuffles it worked.
Mostly because random shuffle uses rand() which is not good enough sometimes. Take a look at one of neal's blog where he describes the good way.
If the randomized solution is expected and it is intended to pass, constrains will be put on a way that the randomized solution has very low chance of failing so no one gets unexpected verdict on the randomized solution. Sometimes TLE solutions may be judged twice to confirm they pass if they are the intended randomized solution.
And yes almost 1 in 10000 solutions will get unlucky. (0.99995050166 in 10000 to be more precise). Which is still fine considering that mostly that won't happen.
There were a lot of people that got WA on system test because of that on this problem: 840D - Судьба.
It happens, but very rarely. You shouldn't worry about it.
The example provided by usernameson shows that sometimes organizers try to fail a particular solution. But then the probability of failing is 1 instead of 1 / 106.
Note there's a difference between
The first ones are good. The second ones can be failed by hacks or authors who predicted your solution
Do organisers actually do things like create anti-random_shuffle test cases? I just assumed such situations arise because a contestant hacks another solution during the contest with an anti-random_shuffle test case and the hack gets added to the system test.
Some do. I wouldn't.
I wouldn't either, but that left me wondering about where exactly is the line.
To give a related example, in my experience people usually think that it is perfectly fine to include an anti-quicksort test that causes a known bad library implementation to run in Theta(n^2).
Why should one be OK and the other not? In both cases you are punishing the same thing -- the solver produced a solution that had the correct algorithm, the mistake was in their implementation, and the mistake was predictable in advance which made it possible to construct a deterministic test case that breaks the solution before the solution existed.
Where should the line be and why? And should the answer be different if the contest system allows for challenges/hacks, which means that other contestants can add those tests anyway?
I don't really have a good answer yet.
I doubt anybody has a good answer.
I would say the special tests shouldn't be created if it's about choosing a seed or a modulo (between two equally-bad possible values). Why should we punish random_shuffle with seed 0, and not with seed 2? Or hashing modulo 109 + 7 and not some other prime? It shouldn't be necessary or useful to choose a strange prime.
Modulo 264 is different because it's not "equally-bad", I would say. But I don't think it's obvious that it should be failed by organizers. And maybe the sorting anti-test is a similar thing to the 264 thing?
On the other hand, maybe organizers should be malicious as much as possible and they should force participants to defend against somebody that tries to predict their exact solution and break it (that's how hacks work for sure). Maybe it's good as a preparation for real life, but it isn't pleasant for beginners. I wouldn't want to care about it in high school, when I started CP. If possible, problems should be about thinking about algorithms instead of thinking what organizers did. This is not a strong argument, though.
There is one important thing to note, algorithms that fail with probability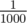 is not that big of a problem. Suppose that a random algorithm have
is not that big of a problem. Suppose that a random algorithm have 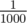 probability of getting the wrong answer, then what you could do is just to run the algorithm a couple of times. Running it 3 times and taking the majority answer will only make it fail with probability
probability of getting the wrong answer, then what you could do is just to run the algorithm a couple of times. Running it 3 times and taking the majority answer will only make it fail with probability 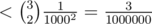 . And if that isn't enough then you could just run it 5 times and fail with probability
. And if that isn't enough then you could just run it 5 times and fail with probability 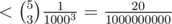 .
.
I don't think that often possible. Usually you either have problems with TL or this is interactive problem where there's a limit on number of queries that you can't use two times
My point was just that algorithms failing with probability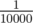 is not a big problem. Lets assume that you are trying to minimize some function and you have a probability of
is not a big problem. Lets assume that you are trying to minimize some function and you have a probability of 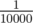 of failing, then simply running it twice will lower that to
of failing, then simply running it twice will lower that to 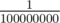 .
.
Also because of this kind of exponential behavior of probabilities, you very seldomly have a small but reasonable probability of failing. You usually fail either very often or pretty much never.
If it's something like checking if matrices multiplication holds (A*B=C) then it's possible. However, solutions like hashing (on a random hash) are hard to do it twice sometimes (or you will end up with TLE because of high constant factor).
Before anyone says, I know that there is something called double-hashing, but hashing already has a big constant factor (because of mods and other thing). Double hashing is not possible it the running time is tight.
Yes, I understand your point. My point is it's not often feasible. E.g if your solution takes 3/4 of TL, you can't run it twice