Hello.
Just started to participate contests to fill 25 participation in codeforces, now I even created my github repository to store my implementation :)
The link is here: https://github.com/McDic/MyImplementations/
Just wanted to show public, you can freely see or criticize my code anytime.
<2019-08-23> Now I have following my own implementations:
- Trie and Aho Corasick
- Segment Tree and Lazy Propagation
- Shortest path algorithms such as Dijkstra and Floyd Warshall
- Disjoint Set Union
- Eratosthenes Sieve (both
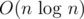and O(n)) - Convex Hull (both Graham Scan and Monotone)
- KMP and Polynomial String Hashing
- Matrix (but no advanced operations yet)
- LCA
- and some other uncompleted stuffs
My further future implementation goal is:
- Minimum Spanning Tree (I don't know why I don't have this in my repository. This is easier, I will implement this asap)
- Heavy Light Decomposition (What the heck this is too hard to implement myself)
- Fast prime decomposition and primality test (like Pollard Rho's, Miller-Rabin primality test)
- Optimized Matrix stuffs (Gaussian elimination, Determinant, etc)
- Big Integers and Fractions with basic arithmetic and comparison operators
- Strongly Connected Components
Thank you for reading this.
One suggestion I have is that if you are building a repository of implementations, why not store the linear O(n) implementation of the Sieve of Erathosthenes :)
Linear sieve? Do you mean Sieve of Eratosthenes?
That's why people would like to see the implementations of a red rather than blue. There are some advanced algorithms you didn't put in your github (Convex Hull, FFT, etc..).
Yeah I know but that's not problem at least I think? I'm just making my own tower to improve my competitive programming skill and I never forced anyone to see mine.
+1 Good luck
Adhami Added n-dimensional dynamic segment tree with generalized feature support and Graham's scan( Convex hull ).
Yes, I meant the Sieve of Erathosthenes but implemented in O(n) time. :)
The reason this is O(N) is because every element is touched at most once. We maintain the invariant that is_prime[x] = false, is done only one time, when we are visiting x's smallest prime factor.
We break when i%primes[j] == 0 because it means that (i*primes[j + 1]) will have the smallest prime factor of primes[j]
Just a suggestion :)
That's interesting. Thank you for providing the code. I will prove myself and implement it later.
ghoshsai5000 Sorry, it seems the algorithm from your code is incorrect. I tried with your code and it says there is a different amount of primes under 2e7. Commented part is your code. (Your code says 4 is prime.)
Hi McDic, I have used this in problems many times. I have also tested it on ideone here to check and it looks fine to me.
Probably, one thing I didn't do in the code snippet I presented was declare the vector 'primes'. I updated it.
Also, could you tell me how many primes there are under 2 × 107 ? I have tested my code here. There might be some bug related to overflow.
Oh it was my mistake! Yeah there are 1270607 primes under 2e7. Sorry to confuse.
I should put your code outside of
if(isPrime[i]), I thought only prime numbers matter to do that.No Worries.
All integers matter here since we are doing it in this way.
Auto comment: topic has been updated by McDic (previous revision, new revision, compare).