Recently, I tried to solve a problem on Atcoder and came up with a solution. I got accepted but have no idea of its complexity. Does anyone know its complexity and when the worst case happens?
Problem:
Given an array with N integers A1, A2, ..., AN and M intervals (L1, R1), ..., (LM, RM), you can perform the following operation arbitrary times:
Choose one of the M intervals (Li, Ri) and add ALi, ALi + 1, ..., ARi by + 1 or - 1.
Is it possible to make all N integers zero?
N, M ≤ 105
My solution:
First of all, if all Li are different, we can uniquely determine how many times we should perform an operation on the interval (Li, Ri) and whether we should choose + 1 or - 1.
Now, we try to avoid the same left bound. When we find two interval (Li, Ri), (Lj, Rj) (Ri < Rj) with the same left bound, i.e. Li = Lj, we change the second interval to (Ri + 1, Rj) (just imagine what happen if we add 1 to (Lj, Rj) and -1 to (Li, Ri)). Because each interval never change its right bound and its left bound is increasing, so we won't do this infinitely.
Here's my implementation: First, we put all right bounds of intervals that have a left bound i into a vector bound[i]. Sort all bound[i]. Starting from bound[0] to bound[100000], we do something likebound[bound[i][j]].push_back(bound[i][j+1]);
It's basically the operation shown in the following picture.
https://drive.google.com/file/d/1q6kYHhXPCIv5N_5qHeWiG6gXrp5KjkkZ/view?usp=sharing
At first, I thought it is a O(n2) but wasn't able to construct a O(n2) test case. After coding it, I got an AC and it only runs less than 100 ms. So what's the complexity?










What about (1, 1), (1, 2), (1, 3), ..., (1, N)?
At first you will have (1, 1), (1, 2), (1, 3), ..., (1, N).
Next, you will have (2, 2), (2, 3), (2, 4), ..., (2, N).
...
You will have (N, N).
So it seems that your algorithm will make O(N2) swaps?
If I have intervals like (3, 4), (3, 8), (3, 13), it will become (3, 4), (4, 8), (8, 13). So in that case, I will have (1, 2), (2, 3), (3, 4), ..., (N - 1, N) instead.
The complexity is actually ! :O For simplicity of notation, I'm going to say there are also N intervals we start with. Now, let's say we are processing the intervals with left endpoint i, and say they are [i, a1], [i, a2], ..., [i, ak] with i < a1 < a2 < ... < ak. Associate interval [i, aj] → [aj - 1, aj].
! :O For simplicity of notation, I'm going to say there are also N intervals we start with. Now, let's say we are processing the intervals with left endpoint i, and say they are [i, a1], [i, a2], ..., [i, ak] with i < a1 < a2 < ... < ak. Associate interval [i, aj] → [aj - 1, aj].
Claim 1: For all but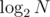 of the intervals [i, a1], [i, a2], ..., [i, ak] their associated interval has length at most half, i.e.
of the intervals [i, a1], [i, a2], ..., [i, ak] their associated interval has length at most half, i.e. 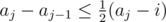 for all but
for all but 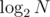 integers 1 ≤ j ≤ k.
integers 1 ≤ j ≤ k.
This is easy to see, as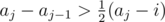 implies that aj - i ≥ 2(aj - 1 - i), so the length was twice as long as the previous interval.
implies that aj - i ≥ 2(aj - 1 - i), so the length was twice as long as the previous interval.
Now, let ti be the number of intervals processed with left endpoint i during the algorithm. Let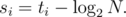 By the above claim, at least si intervals' lengths were halved after processing i. As we started with N intervals and never have more, and each interval can only get halved
By the above claim, at least si intervals' lengths were halved after processing i. As we started with N intervals and never have more, and each interval can only get halved 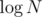 times, we have that
times, we have that 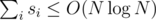 , so
, so 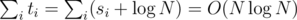 also.
also.
Thanks!
Hope for a link to this problem.
Well...I hope I won't spoil it because this is not exactly the same as the problem I described. https://atcoder.jp/contests/cf17-final-open/tasks/cf17_final_e