Recently i got a task from my teacher: Given two numbers n and m(10^10<=n<=10^11. 1<=m<=10^5) Find all prime numbers in range [n, n + m].
1 sec, 32 mb
Help plz
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Recently i got a task from my teacher: Given two numbers n and m(10^10<=n<=10^11. 1<=m<=10^5) Find all prime numbers in range [n, n + m].
1 sec, 32 mb
Help plz
| Name |
|---|



Use segmented sieve, here's a nice tutorial on it: https://forthright48.com/2015/09/segmented-sieve-of-eratosthenes.html
Note that if an integer x in the range [n, n + m] is non-prime, than it should be divisible by some prime number p ≤ P, where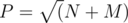 , N = 1011 and M = 105. Hence, the required numbers may be found by excluding all non-prime numbers in this range. The performance of the solution may be improved by observing that all the required numbers are odd numbers. A non-prime odd number is the product of two odd numbers.
, N = 1011 and M = 105. Hence, the required numbers may be found by excluding all non-prime numbers in this range. The performance of the solution may be improved by observing that all the required numbers are odd numbers. A non-prime odd number is the product of two odd numbers.