Hi there!
During preparation of Oleksandr Kulkov Contest 1 I started writing some template for polynomial algebra (because 3 problems in contest in one or another way required some polynomial operations). And with great pleasure I'd like to report that it resulted in this article on cp-algorithms.com (English translation for e-maxx) and this mini-library containing all mentioned operations and algorithms (except for Half-GCD algorithm). I won't say the code is super-optimized, but at least it's public, provides some baseline and is open for contribution if anyone would like to enhance it!
Article also provides some algorithms I didn't mention before. Namely:
- Interpolation: Now the described algorithm is
and not 
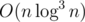as it was before. - Resultant: Given polynomials A(x) and B(x) compute product of A(μi) across all μi being roots of B(x).
- Half-GCD: How to compute GCD and resultants in (just key ideas).
Feel free to read the article to know more and/or use provided code :)
tl;dr. article on operations with polynomials and implementation of mentioned algorithms.
What?! That's the best and most useful article I've ever seen in my life, and it helped me so many times in so many ways, and now I've found that it's yours. It's even funnier because I'm not even sure if it's a surprise for me. Respect!
Also, CF warned me about necroposting, but I think that this blog/article is too good to be forgotten.
Nice to know you're still a fan of my articles. I wonder how you timed your response just 5 minutes before I posted something else about polynomials and convolutions :)
This is super helpful.
Bookmark on cp-algorithms for section with API + implementation, since the old github links are not working
FYI: there is no topic about Polynomials on USACO guide (except FFT), in case somebody wants to contribute.
PS: For interpolation, this blog also has a nice explanation with sample problems: https://codeforces.net/blog/entry/82953