→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3885 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3580 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3506 |
| 7 | ecnerwala | 3505 |
| 8 | Radewoosh | 3457 |
| 9 | Kevin114514 | 3377 |
| 10 | gamegame | 3374 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 170 |
| 2 | Um_nik | 162 |
| 3 | -is-this-fft- | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | maomao90 | 155 |
| 8 | adamant | 154 |
| 9 | luogu_official | 153 |
| 10 | awoo | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 01.01.2025 02:10:28 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Можно ли завалить бин. поиск для 500, который считает сумму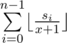 в
в
int?Попробуем доказать от противного.
Пусть текущая сумма больше 2000000000 (переполнение). Тогда сумма на предыдущем шаге бинпоиска должна быть максимум в два раза меньше (поскольку делится, в худшем случае, на число 2x+1), то есть, больше миллиарда, а это бинпоиск отсечёт.
Кстати, извиняюсь за вопрос, но контест ведь нерейтинговый? Не нашёл информацию в правилах.
Вполне себе рейтинговый.
а если предыдущая сумма больше миллиарда больше и 2 миллиардов?
Ну, в самом начале бинпоиска переполнения у нас нет (максимальная сумма равна 2 * 47), а выше показано, что оно не может за один ход возникнуть из суммы, меньшей миллиарда. Возможно, ошибся где-то в доказательстве, но у меня только что с интом зашло.
это смотря какие границы у Вашего бинпоиска, если идти с середины (5e8) и спускаться до нуля, то это как уже сказано ранее невозможно, ибо сумма возрастает каждый раз не более чем вдвое. значит когда-то переполнится(станет больше k)
Я завалил свой бинпоиск и еще парочку решений в комнате, но все бинпоиск пишут по разному. Некоторые решения даже прошли сис. тесты с переполнением.
у меня в комнате у чувака упало решение потому что он границы бинпоиска сделал [-1,1000000000], а не [0,1000000000] и считал в интах. считал бы в лонгах или сделал нормальные границы, тогда бы прошло
How to solve the 1000 point problem ...
I'd like to know too...
It's easy to calculate the expectancy of attacked cells if you only place only one knight. If I'm not mistaken, it's (8*N^2 — sigma(1,8) f(i)) / N^2, where f(i) is the amount of cells from which the knight cannot make move i (the knight can move in 8 different ways). For each of the 8 types of movement, you define the rectangular region from which the knight cannot make that move (it's always rectangular, covers either the whole horizontal range or the whole vertical range, and starts from one corner of the board, depending on the type of move), then f(i) is the area of that rectangle.
But when the second knight comes into the game, it changes completely and I don't know how to solve it...
First, let's solve problem "what is probability of cell (i; j) to be under attack? (call it p_i_j)". Calculate number of different cells (x, y), that if there is a knight on cell (x, y), cell (i, j) is under attack. Let it be A. Than p_i_j = (total — (n^2 — A) * (n^2 — A — 1) / 2) / total, where total = n^2 * (n^2 — 1) / 2 — number of different arrangements of knights.
Now, we just need to calculate sum of p_i_j over all n^2 cells. We know that p_i_j depends only on A (number of different...). So let's divide all cells in groups with same value of A. Let's call value i interesting if exist such j that A[i][j] != A[i-1][j]. We can find that only {0, a, b, n — a, n — b, n} (may be +-1 in some of them) can be interesting. So if we divide our board into count_interesting^2 parts, for every part we could calculate p_i_j in some cell and multiply it by number of cells in part.