
As the round is over, the links are disabled by them.
I can only come up with a very basic brute force solution of $$$(2*N)!$$$ where for each of the order of visiting I calculate the cost and then update the answer accordingly. But as expected this even didn't pass even a single test.
Can someone please help me with some spoilers on how to proceed further with it?
Thanks!
Edit: Hello all! Why everyone is downvoting the post? Is there something wrong with it or I asked the question in a wrong way ? I find the problem difficult so I asked for help and if someone find it easy then instead of directly downvoting please explain the solution (or atleast a step towards it) and then downvote if you think it's irrelevant.











Auto comment: topic has been updated by pk842 (previous revision, new revision, compare).
I think an algorithm for this can solve hamiltonian path problem. So I don't think that a polynomial time solution exists.
News in 3 days: Samsung engineers solved P = NP
Really it doesn't have any polynomial time solution?
But there are people who solved it fully. Don't know..
Probably it does have some polynomial time solution, since it is asking for the placement of starting location, and not actual length.
Look at the output format. Seems that it does ask for length.
thonk
I guess you're right
if this means the cities should be visited in the order it is given in input then polynomial time algorithm does exist.
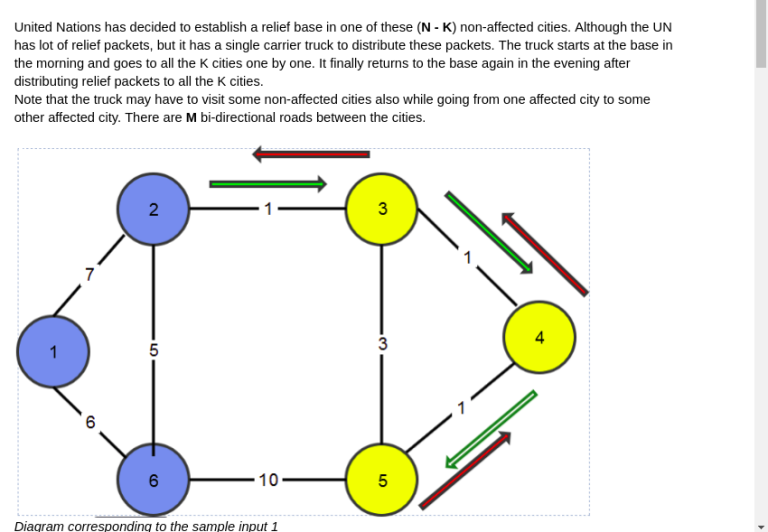
There are some inconsistencies in the statement, for example: the input description says there will be K integers in K lines, but sample gives all K integers in single line.
Any hints towards solution?
Find all pair shortest paths in $$$O(n^2\log n)$$$. Sum up distances between adjacent pair of nodes, and add minimum distance from a node of those $$$N-K$$$ nodes to first and last node of those $$$K$$$ nodes.
how to distinguish the first and last node of $$$K$$$ nodes? Or did you mean to try all possible pairs.
And also can you please explain "Sum up distances between adjacent pair of nodes" a little bit more?
Off-topic : Were you eligible(exp.-wise) for interview or appeared in contest just for fun ? It was mentioned that this contest was for experienced candidates, so I didn't participate.
I participated just for sake of practice.