Dear codeforces,
I am writing to seek help from everyone in cf to find the optimal time complexity for the following problem.
Given the following inputs,
The first line contains an integer $$$n$$$, the total numbers of points in the 2D-plane.
The next $$$n$$$ lines contain 2 integers each. The $$$i^{th}$$$ ($$$0 \leq i < n$$$) of them contains 2 space-separated integers $$$p_{i_x}$$$, $$$p_{i_y}$$$ , the x and y coordinates of point $$$p_i$$$. Note that $$$i$$$ is also the id of the point $$$p_i$$$.
The next line contains an integer $$$q$$$, the number of queries.
The next $$$q$$$ lines contain 2 integers each.The $$$j^{th}$$$ ($$$1 \leq i \leq q$$$) of them contains 2 space-separated integers $$$l_j$$$, $$$r_j$$$, a range of points from the id $$$l_j$$$ to id $$$r_j$$$ ($$$0 \leq l_j, r_j < n$$$ and $$$3 \leq r_j - l_j + 1 \leq n$$$ ).
Please output the answer with the following requirements:
For the $$$j^{th}$$$ line, which is the $$$j^{th}$$$ query ($$$1 \leq j \leq q$$$), find and output the area of the convex hull of the set of points $$$p_i$$$ in range $$$l_j \leq i \leq r_j$$$ of the id.
Example
| Input 1 | Output 1 |
|---|---|
| 7 1 1 3 0 2 2 3 5 5 4 6 2 4 2 3 2 6 2 7 1 7 | 10 11.5 14 |
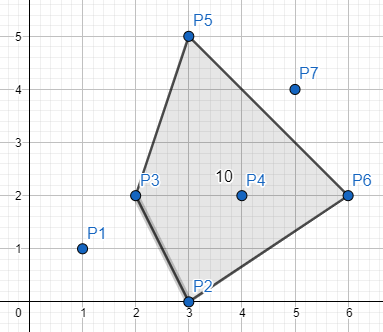
l=2, r=6 => area=10
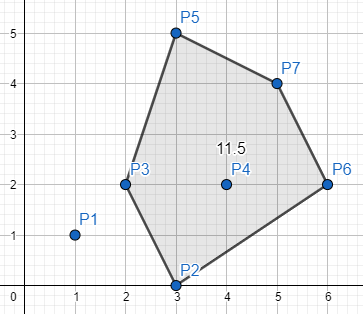
l=2, r=7 => area=11.5
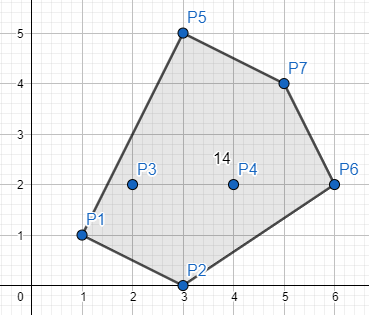
l=1, r=7 => area=14











Apply Mo's algorithm
Now we have to support insert and delete queries
Use Dynamic connectivity trick to become all inserts (search for blogs about it)
Doing all insert is kinda possible with a Lichao Segtree (Persistent)
So we have a $$$O(n^{1.5} log^{2}n)$$$ solution which i don't think would be faster than just doing each query seperately in $$$O(n^2)$$$ (sort nodes before answering query so that you can do $$$O(n)$$$ each query)
I hope for $$$O(nlog^kn)$$$ solutions
WoW, great thanks for your concise solution. Btw is there exist an online solution which has the similar time complexity with your offline one?
I have an $$$O(n^{1.5}logn)$$$ solution, but it uses $$$O(n^{1.5}logn)$$$ memory, so in my opinion it is worse than the above thingy.
Break the array into B blocks. For every pair of blocks, compute their convex hull with all blocks in between those two, also using a persistent LiChao. It uses $$$O(n^2logn/B)$$$ time.
To answer queries, just find the corresponding pair of blocks, then insert the remaining O(B) points into the lichao tree. It uses $$$O(QBlogn)$$$
So we can pick $$$B$$$ to be the square root of $$$n$$$ and obtain $$$O(n^{1.5}logn)$$$
I have a $$$\Omega(n^{1.5})$$$ lower bound for any solution that computes area by decomposing into trapezoids (or equivalent).
Here is a case where there are $$$\Theta(n^{1.5})$$$ distinct edges on $$$\Theta(n)$$$ convex hulls:
Take a convex polygon with $$$n$$$ vertices and divide it into $$$\sqrt{n}$$$ sections. Let's build the array in $$$\sqrt{n}$$$ blocks. The $$$i$$$ th block will contain the $$$i$$$ th point from each section. The queries are all $$$\Theta(n)$$$ possible queries that contain only complete blocks.
Let's count the edges connecting points in different sections. For each of the $$$\sqrt{n}$$$ pairs of adjacent sections, there are $$$\Theta(n)$$$ such edges.
This doesn't prove that a $$$o(n^{1.5})$$$ solution is impossible, but I've never seen any way of computing area without looking at all the edges (If anyone has I would be interested).
Edit: Actually, I think I have a reduction from matrix multiplication.
In the case described above, further require that all points in a section be collinear and all queries include the middle block. Define the master polygon to be the polygon whose sides are the lines containing each section. We can compute the area of a query polygon as the area of the master polygon minus some corner triangles. The area of a corner triangle is proportional to the product of the distances of the points to the vertices of the master polygon. The result of the query will be in the form $$$\Sigma_k{a_{ki}b_{kj}}$$$, where we are free to choose basically arbitrary values for $$$a_{ki}$$$ and $$$b_{kj}$$$ ($$$k$$$ ranges over sections and $$$i$$$ and $$$j$$$ range over blocks). This is $$$\Theta(\sqrt{n})$$$ by $$$\Theta(\sqrt{n})$$$ matrix multiplication.
This gives a lower bound of $$$\Omega(n^\frac{\omega}{2})$$$, so I wouldn't hope for a $$$O(n\log^k{n})$$$ solution anytime soon.
Hi. Which tool did you use to draw the polygons?
I guess it's Geogebra.