Link: https://www.hackerrank.com/challenges/tree-pruning
This question has been solved using DP by most of the users, but I was wondering if this could be solved using Greedy. I came up with an approach using Greedy, which failed most of the test cases. But I couldn't come up with a small counter case where Greedy won't work.
My Greedy Approach:
- Find $$$sum$$$ for all nodes, where $$$sum$$$ for a node denotes the sum of values of all its children.
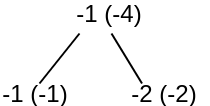
($$$sum$$$ for nodes written in brackets)
2. Now get the subtree with minimum {sum, val}, where $$$val$$$ denotes value of node, and $$$sum$$$ is defined above. ({a, b} denotes a pair in C++).
3. if sum is positive break, without removing, else remove that subtree.
4. Go back to Step 1.
Above loop is run at most k times.
Any help in finding a small counter case, and why it won't work will be helpful.
Smallest Test Case for which the above approach failed on Hackerrank:
20 5
773581246 -348306003 -788117784 629111611 -142726426 241605607 418519531 -291199082 -453706450 -850635818 -641575760 453047217 -874946563 -257858612 927125122 860575225 -162713554 61368550 -262466871 361084678
2 1
3 2
4 2
5 1
6 3
7 2
8 1
9 6
10 7
11 8
12 1
13 7
14 10
15 3
16 14
17 14
18 15
19 17
20 3











Here's the case I found:
Your program outputs 1 but other AC Codes outputs 2. I'll update you more when I'm clear about why this is so.
Update: if you look at the subtree rooted at 2, it's sum is (-2 + -2 + -2 + 3) = -3, which is the most negative among all subtrees. If you remove it, you're left with node 1, hence your code's answer is 1.
However, you can instead spend 2 operations to remove nodes 3 and 5, which gives you the remaining nodes 1, 2, 4. The sum of weights in this case is 2.
Thank You very much, Got it.