Idea: awoo
Tutorial
Tutorial is loading...
Solution (pikmike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
int main() {
int tc;
scanf("%d", &tc);
while (tc--){
int n;
scanf("%d", &n);
int p = 0, c = 0;
bool fl = true;
forn(i, n){
int x, y;
scanf("%d%d", &x, &y);
if (x < p || y < c || y - c > x - p)
fl = false;
p = x, c = y;
}
puts(fl ? "YES" : "NO");
}
return 0;
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
fun main() {
val T = readLine()!!.toInt()
for (tc in 1..T) {
val (n, x) = readLine()!!.split(' ').map { it.toInt() }
val a = readLine()!!.split(' ').map { it.toInt() }.sortedDescending()
var cnt = 0
var sum = 0L
while (cnt < n && sum + a[cnt] >= (cnt + 1) * x.toLong()) {
sum += a[cnt]
cnt++
}
println(cnt)
}
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (Ne0n25)
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); ++i)
typedef long long li;
const int N = 300 * 1000 + 13;
int n;
li a[N], b[N];
void solve() {
scanf("%d", &n);
forn(i, n) scanf("%lld%lld", &a[i], &b[i]);
li ans = 0, mn = 1e18;
forn(i, n) {
int ni = (i + 1) % n;
li val = min(a[ni], b[i]);
ans += a[ni] - val;
mn = min(mn, val);
}
ans += mn;
printf("%lld\n", ans);
}
int main() {
int T;
scanf("%d", &T);
forn(i, T)
solve();
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define x first
#define y second
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
int n;
li l, r;
inline bool read() {
if(!(cin >> n >> l >> r))
return false;
return true;
}
bool intersect(li l1, li r1, li l2, li r2) {
return min(r1, r2) > max(l1, l2);
}
vector<int> ans;
void calc(int lf, int rg, li &id) {
if(lf == rg) return;
if(intersect(l, r, id, id + 2 * (rg - lf))) {
fore(to, lf + 1, rg + 1) {
if(l <= id && id < r)
ans.push_back(lf);
id++;
if(l <= id && id < r)
ans.push_back(to);
id++;
}
} else
id += 2 * (rg - lf);
calc(lf + 1, rg, id);
if(lf == 0) {
if(l <= id && id < r)
ans.push_back(lf);
id++;
}
}
inline void solve() {
ans.clear();
li id = 0;
l--;
calc(0, n - 1, id);
assert(sz(ans) == r - l);
assert(id == n * li(n - 1) + 1);
for(int v : ans)
cout << v + 1 << " ";
cout << endl;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
int tt = clock();
#endif
ios_base::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cout << fixed << setprecision(15);
int tc; cin >> tc;
while(tc--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (pikmike)
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int MOD = 998244353;
int add(int a, int b){
a += b;
if (a >= MOD)
a -= MOD;
if (a < 0)
a += MOD;
return a;
}
int mul(int a, int b){
return a * 1ll * b % MOD;
}
int binpow(int a, int b){
int res = 1;
while (b){
if (b & 1)
res = mul(res, a);
a = mul(a, a);
b >>= 1;
}
return res;
}
int main() {
long long d;
scanf("%lld", &d);
int q;
scanf("%d", &q);
vector<long long> primes;
for (long long i = 2; i * i <= d; ++i) if (d % i == 0){
primes.push_back(i);
while (d % i == 0) d /= i;
}
if (d > 1){
primes.push_back(d);
}
vector<int> fact(100), rfact(100);
fact[0] = 1;
for (int i = 1; i < 100; ++i)
fact[i] = mul(fact[i - 1], i);
rfact[99] = binpow(fact[99], MOD - 2);
for (int i = 98; i >= 0; --i)
rfact[i] = mul(rfact[i + 1], i + 1);
forn(i, q){
long long x, y;
scanf("%lld%lld", &x, &y);
vector<int> up, dw;
for (auto p : primes){
int cnt = 0;
while (x % p == 0){
--cnt;
x /= p;
}
while (y % p == 0){
++cnt;
y /= p;
}
if (cnt < 0) dw.push_back(-cnt);
else if (cnt > 0) up.push_back(cnt);
}
int ans = 1;
ans = mul(ans, fact[accumulate(up.begin(), up.end(), 0)]);
for (auto it : up) ans = mul(ans, rfact[it]);
ans = mul(ans, fact[accumulate(dw.begin(), dw.end(), 0)]);
for (auto it : dw) ans = mul(ans, rfact[it]);
printf("%d\n", ans);
}
return 0;
}
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
typedef long long li;
const li INF64 = li(1e18);
const int N = 500043;
li f[N];
li get(int x)
{
li ans = 0;
for (; x >= 0; x = (x & (x + 1)) - 1)
ans += f[x];
return ans;
}
void inc(int x, li d)
{
for (; x < N; x = (x | (x + 1)))
f[x] += d;
}
li get(int l, int r)
{
return get(r) - get(l - 1);
}
li dp[N];
int a[N], b[N], p[N];
int n, m;
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
for(int i = 0; i < n; i++)
scanf("%d", &p[i]);
scanf("%d", &m);
for(int i = 0; i < m; i++)
scanf("%d", &b[i]);
for(int i = 0; i < n; i++)
dp[i] = -INF64;
map<int, vector<int> > pos;
for(int i = 0; i < n; i++)
pos[a[i]].push_back(i);
set<pair<int, int> > q;
for(int i = 0; i < n; i++)
q.insert(make_pair(a[i], i));
for(auto x : pos[b[0]])
dp[x] = p[x];
while(!q.empty() && q.begin()->first <= b[0])
{
int k = q.begin()->second;
q.erase(q.begin());
if(p[k] > 0)
inc(k, p[k]);
}
for(int i = 1; i < m; i++)
{
int i1 = b[i - 1], i2 = b[i];
vector<int> both_pos;
for(auto x : pos[i1])
both_pos.push_back(x);
for(auto x : pos[i2])
both_pos.push_back(x);
li best = -INF64;
int last = -1;
sort(both_pos.begin(), both_pos.end());
for(auto x : both_pos)
{
best += get(last + 1, x);
last = x;
if(a[x] == i1)
best = max(best, dp[x]);
else
dp[x] = best + p[x];
}
while(!q.empty() && q.begin()->first <= i2)
{
int k = q.begin()->second;
q.erase(q.begin());
if(p[k] > 0)
inc(k, p[k]);
}
}
li best_dp = -INF64;
for(int i = 0; i < n; i++)
if(a[i] == b[m - 1])
best_dp = max(best_dp, dp[i] + get(i + 1, n - 1));
li ans = 0;
for(int i = 0; i < n; i++)
ans += p[i];
ans -= best_dp;
if(ans > li(1e15))
puts("NO");
else
printf("YES\n%lld\n", ans);
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
#define forn(i, n) for(int i = 0; i < n; i++)
#define sz(a) ((int)(a).size())
const int LOGN = 20;
const int N = (1 << LOGN);
typedef long double ld;
typedef long long li;
const ld PI = acos(-1.0);
struct comp
{
ld x, y;
comp(ld x = .0, ld y = .0) : x(x), y(y) {}
inline comp conj() { return comp(x, -y); }
};
inline comp operator +(const comp &a, const comp &b)
{
return comp(a.x + b.x, a.y + b.y);
}
inline comp operator -(const comp &a, const comp &b)
{
return comp(a.x - b.x, a.y - b.y);
}
inline comp operator *(const comp &a, const comp &b)
{
return comp(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);
}
inline comp operator /(const comp &a, const ld &b)
{
return comp(a.x / b, a.y / b);
}
vector<comp> w[LOGN];
vector<int> rv[LOGN];
void precalc()
{
for(int st = 0; st < LOGN; st++)
{
w[st].assign(1 << st, comp());
for(int k = 0; k < (1 << st); k++)
{
double ang = PI / (1 << st) * k;
w[st][k] = comp(cos(ang), sin(ang));
}
rv[st].assign(1 << st, 0);
if(st == 0)
{
rv[st][0] = 0;
continue;
}
int h = (1 << (st - 1));
for(int k = 0; k < (1 << st); k++)
rv[st][k] = (rv[st - 1][k & (h - 1)] << 1) | (k >= h);
}
}
inline void fft(comp a[N], int n, int ln, bool inv)
{
for(int i = 0; i < n; i++)
{
int ni = rv[ln][i];
if(i < ni)
swap(a[i], a[ni]);
}
for(int st = 0; (1 << st) < n; st++)
{
int len = (1 << st);
for(int k = 0; k < n; k += (len << 1))
{
for(int pos = k; pos < k + len; pos++)
{
comp l = a[pos];
comp r = a[pos + len] * (inv ? w[st][pos - k].conj() : w[st][pos - k]);
a[pos] = l + r;
a[pos + len] = l - r;
}
}
}
if(inv) for(int i = 0; i < n; i++)
a[i] = a[i] / n;
}
comp aa[N];
comp bb[N];
comp cc[N];
inline void multiply(comp a[N], int sza, comp b[N], int szb, comp c[N], int &szc)
{
int n = 1, ln = 0;
while(n < (sza + szb))
n <<= 1, ln++;
for(int i = 0; i < n; i++)
aa[i] = (i < sza ? a[i] : comp());
for(int i = 0; i < n; i++)
bb[i] = (i < szb ? b[i] : comp());
fft(aa, n, ln, false);
fft(bb, n, ln, false);
for(int i = 0; i < n; i++)
cc[i] = aa[i] * bb[i];
fft(cc, n, ln, true);
szc = n;
for(int i = 0; i < n; i++)
c[i] = cc[i];
}
comp a[N];
comp b[N];
comp c[N];
vector<int> p_function(const vector<int>& v)
{
int n = v.size();
vector<int> p(n);
for(int i = 1; i < n; i++)
{
int j = p[i - 1];
while(j > 0 && v[j] != v[i])
j = p[j - 1];
if(v[j] == v[i])
j++;
p[i] = j;
}
return p;
}
int p[26];
char buf[N];
string s, t;
int main()
{
precalc();
for(int i = 0; i < 26; i++)
{
scanf("%d", &p[i]);
p[i]--;
}
scanf("%s", buf);
s = buf;
scanf("%s", buf);
t = buf;
int n = s.size();
int m = t.size();
vector<int> color(26, 0);
vector<vector<int> > cycles;
for(int i = 0; i < 26; i++)
{
if(color[i])
continue;
vector<int> cycle;
int cc = cycles.size() + 1;
int cur = i;
while(color[cur] == 0)
{
cycle.push_back(cur);
color[cur] = cc;
cur = p[cur];
}
cycles.push_back(cycle);
}
vector<int> ans(m - n + 1);
vector<int> s1, t1;
for(int i = 0; i < n; i++)
s1.push_back(color[int(s[i] - 'a')]);
for(int i = 0; i < m; i++)
t1.push_back(color[int(t[i] - 'a')]);
vector<int> st = s1;
st.push_back(0);
for(auto x : t1)
st.push_back(x);
vector<int> pf = p_function(st);
for(int i = 0; i < m - n + 1; i++)
if(pf[2 * n + i] == n)
ans[i] = 1;
map<char, comp> m1, m2;
for(auto cur : cycles)
{
int k = cur.size();
for(int i = 0; i < k; i++)
{
ld ang1 = 2 * PI * i / k;
ld ang2 = (PI - 2 * PI * i) / k;
m1[char('a' + cur[i])] = comp(cosl(ang1), sinl(ang1));
m2[char('a' + cur[i])] = comp(cosl(ang2), sinl(ang2));
}
}
ld ideal = 0;
for(int i = 0; i < n; i++)
ideal += (m1[s[i]] * m2[s[i]]).x;
reverse(s.begin(), s.end());
for(int i = 0; i < n; i++)
a[i] = m1[s[i]];
for(int i = 0; i < m; i++)
b[i] = m2[t[i]];
int szc;
multiply(a, n, b, m, c, szc);
for(int i = 0; i < m - n + 1; i++)
if(fabsl(c[i + n - 1].x - ideal) > 0.01)
ans[i] = 0;
for(int i = 0; i < m - n + 1; i++)
printf("%d", ans[i]);
return 0;
}










Can someone give a proof why the path $$$x\rightarrow \gcd(x,y)\rightarrow y$$$ is shortest in problem E?
Anyway, interesting problem set although with some difficulties on system test.
Whenever you move along an edge, some numbers are either added to the set of divisors of the current vertex, or removed from it (and the cost of the edge is the number of affected elements). So, ideally you want your path to have length equal to $$$d(x) + d(y) - 2d(gcd(x, y))$$$, where $$$d(i)$$$ is the number of divisors of $$$i$$$.
If you go through $$$gcd(x, y)$$$, then all divisors of $$$x$$$ which are not divisors of $$$y$$$ are removed, then all remaining divisors of $$$d(y)$$$ are added, so the path has length $$$d(x) + d(y) - 2d(gcd(x, y))$$$, which is optimal. But if you don't go through $$$gcd(x, y)$$$, then you either go through one of its divisors (thus removing $$$gcd(x, y)$$$ from the set, so the length is greater than optimal), or go through some number which is neither a divisor of $$$x$$$ nor a divisor of $$$y$$$.
How it compares to $$$x\rightarrow lcm(x,y)\rightarrow y$$$? The length is $$$2d(lcm(x,y))-d(x)-d(y)$$$, which for me is not easy to tell if it's shorter or longer.
Going through $$$lcm(x, y)$$$ obviously adds $$$lcm(x, y)$$$ to the list of divisors, and we have to remove it afterwards, that's why it's suboptimal.
Reformulate the query problem: we have two numbers $$$a$$$ and $$$b$$$ and want to get $$$b$$$ from $$$a$$$. We can do it only by modifying or dividing a by prime number. Every change costs difference between each number divisor's count.
Calculate change's cost
We could represent any number $$$n$$$ like $$$n=p_1^{l_1}p_2^{l_2}...p_n^{l_n}$$$ ($$$l_i$$$ can be 0, it means $$$p_i$$$ isn't a divisor of $$$n$$$)
Count of divisors, let's name it $$$d(n)$$$, it will be $$$d(n)$$$ = $$$(l_1+1)(l_2+1)...(l_n+1)$$$. When we change $$$a$$$ to $$$b$$$ by modifying we waste $$$d(b) - d(a)$$$.
$$$a=p_1^{l_1}p_2^{l_2}...p_i^{l_i}...p_n^{l_n}$$$
$$$b=p_1^{l_1}p_2^{l_2}...p_i^{l_i+1}...p_n^{l_n}$$$
As we have seen, we have modified by $$$p_i$$$. Calculate divisor's difference: $$$d(b) - d(a) = (l_1+1)(l_2+1)...(l_{i-1}+1)(l_{i+1}+1)... (l_n+1) = \frac{d(a)}{(l_i+1)}$$$ For dividing it works in opposite way: we waste $$$d(a) - d(b)$$$.
$$$Observation 1$$$: if we during our changes have modified and divided by some prime number we could not do these two operations.
$$$Proof$$$. Consider changes between these two changes. $$$x➔xq➔x_1q➔...➔x_nq➔x_n$$$, if we delete first and latest operations we have: $$$x➔x_1➔...➔x_n$$$.
Compare costing changes $$$x_iq➔x_{i+1}q$$$ and $$$x_i➔x_{i+1}$$$ by modifying by $$$p≠q$$$.
$$$d(x_{i+1}q)-d(x_iq) = \frac{d(x_iq)}{l+1}$$$
$$$d(x_{i+1})-d(x_i) = \frac{d(x_i)}{l+1}$$$
$$$l$$$ is a power of $$$p$$$ in canonical representation of number $$$x_i$$$ and $$$x_iq$$$, $$$l$$$ is the same because $$$l$$$ only changes if $$$p=q$$$ $$$\frac{d(x_iq)}{l+1} > \frac{d(x_i)}{l+1}$$$, so better do in second way.
$$$Observation 2:$$$ it is better firstly to do dividing by prime numbers, which aren't divisors of $$$b$$$, then do modifying until we get $$$b$$$.
$$$Proof.$$$ Consider the simplest example: $$$a = pc$$$, $$$b=qc$$$, where $$$p$$$ and $$$q$$$ are prime numbers. Notice $$$c = gcd(a,b)$$$. If we firstly modify and then divide our changes will be $$$a➔pcq➔b$$$. We waste $$$2*d(pcq) - d(a) - d(b)$$$.
If we firstly divide and then modify our changes will be $$$a➔c➔b$$$. We waste $$$d(a) + d(b) + 2d(c)$$$.
Subtract second equation from first one:
$$$2d(pcq) - 2d(a) - 2d(b) + 2d(c)$$$
$$$(d(pcq) - d(a)) - (d(b) - d(c))$$$, substitute $$$a=pc$$$ and $$$b=qc$$$
$$$(d(pcq) - d(pc)) - (d(qc) - d(c))$$$
$$$d(pcq) - d(pc) = \frac{d(pc)}{l_q+1}$$$, $$$d(qc) - d(c) = \frac{d(c)}{l_q+1}$$$, where $$$l_q$$$ is a power of $$$q$$$ in canonical representation of number $$$pcq$$$ and $$$qc$$$.
Numbers $$$pc$$$ and $$$c$$$ have same $$$l_q$$$, so $$$d(pcq) - d(pc) - d(qc) + q(c) = \frac{d(pc) - d(c)}{l_q+1}$$$ and it is bigger then zero, so $$$d(a) + d(b) + 2d(c)$$$ is less then $$$2d(pcq) - d(a) - d(b)$$$, so better firstly to divide and then modify.
$$$UPD: $$$
$$$Obseravation3:$$$ if we during our change have divided and modified by some number we could not do these two operations.
$$$Proof.$$$
Consider changes between these two change: $$$xq➔x➔x_1➔...➔x_n➔x_nq$$$. If we detele first and last operations we have: $$$x_q➔x_1q➔x_2q➔...➔x_n➔x_nq$$$. Name them $$$changing$$$ $$$paths$$$.
Using $$$obseravation 2$$$ we know to get optimal $$$changing$$$ $$$path$$$ firstly we do dividing, then do modifying. Our $$$changing$$$ $$$paths$$$ can be represented like:
$$$xq➔x➔x_1➔...➔x_k➔..➔x_n➔x_nq$$$
and $$$x_q➔x_1q➔x_2q➔...➔x_kq➔..➔x_{n}q➔x_nq$$$.
We do only dividing to get $$$x_kq$$$ and $$$x_k$$$ and then only modifying.
Calculate sum of changing costs in first $$$changing$$$ $$$path$$$:
$$$(d(xq)-d(x))+(d(x)-d(x_1))+...+(d(x_{k-1})-d(x_k))+(d(x_{k+1})-d(x_k))+$$$ $$$+...+(d(x_n) -d(x_n-1))+(d(x_nq)-d(x_n))=$$$ $$$\frac{d(x)}{l+1}+\frac{d(x_1)}{l_1+1}+...+\frac{d(x_{k-1})}{l_{k-1}+1}+\frac{2d(x_k)}{l_k+1}+\frac{d(x_{k+1}}{l_{k+1}}+...+\frac{d(x_n-1)}{l_{n-1}}+ \frac{d(x_n)}{l+1}= \frac{d(x)}{l+1}+\frac{d(x_n)}{l+1}+\sum\limits_{i=1}^k\frac{d(x_i)}{l_i+1}+\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{l_i+1}$$$
Notice in first and last fractions the denominator is the same because when we change $$$xq➔x$$$ and $$$x_n➔x_nq$$$ we divide and modify by same prime number $$$q$$$. In general, when we change $$$x_i➔xq_i$$$ or $$$xq_i➔x_i$$$ we waste $$$\frac{d(x_i)}{l+1}$$$.
Calculate sum of chaging costs in second $$$changing$$$ $$$path$$$: $$$(d(xq)-d(x_1q)) +...+(d(x_{k-1}q) - d(x_kq)) + (d(x_{k+1}q) - d(x_kq)) +...+(d(x_nq) -d(x_{n-1}q))=$$$ $$$\sum\limits_{i=1}^k\frac{d(x_iq)}{l_i+1}+\sum\limits_{i=k}^{n-1}\frac{d(x_iq)}{l_i+1}$$$
Subtact first equation from second:
$$$\frac{d(x)}{l+1}+\frac{d(x_n)}{l+1}-(\sum\limits_{i=1}^k\frac{d(x_iq)}{l_i+1}-\sum\limits_{i=1}^k\frac{d(x_i)}{l_i+1})-(\sum\limits_{i=k}^{n-1}\frac{d(x_iq)}{l_i+1}-\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{l_i+1})$$$
Since $$$d(x_iq)-d(x_i)=\frac{d(x_i)}{l+1}$$$, so we get $$$\frac{d(x)}{l+1}+\frac{d(x_n)}{l+1}-\sum\limits_{i=1}^k\frac{d(x_i)}{(l_i+1)(l+1)}-\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{(l_i+1)(l+1)}$$$, by modifying by $$$l+1$$$ we get: $$$d(x)+d(x_n)-\sum\limits_{i=1}^k\frac{d(x_i)}{l_i+1}-\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{l_i+1}$$$
Separately calculate $$$d(x)-\sum\limits_{i=1}^k\frac{d(x_i)}{l_i+1}$$$ and $$$d(x_n)-\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{l_i+1}$$$:
Since $$$d(x_i)-d(x_{i-1}) = \frac{x_i}{l_i+1}$$$, so $$$d(x_i) = \frac{d(x_{i+1})(l_i+2)}{l_i+1}$$$
$$$d(x)-\sum\limits_{i=1}^k\frac{d(x_i)}{l_i+1} = d(x)-\frac{d(x_1)}{l_1+1}-\sum\limits_{i=2}^k\frac{d(x_i)}{l_i+1}=\frac{d(x_1)(l_1+2)}{l_1+1}-\frac{d(x_1)}{l_1+1}-\sum\limits_{i=2}^k\frac{d(x_i)}{l_i+1}=$$$ $$$\frac{d(x_1)(l_i+1)}{l_i+1}$$$-$$$\sum\limits_{i=2}^k\frac{d(x_i)}{l_i+1}=$$$ $$$d(x_1)-\sum\limits_{i=2}^k\frac{d(x_i)}{l_i+1}$$$
If we go on in the end we will get $$$d(x_k)$$$
Similarly we calculate $$$d(x_n)-\sum\limits_{i=k}^{n-1}\frac{d(x_i)}{l_i+1}=$$$ $$$\frac{d(x_n)(l_{n-1}+2)}{l_{n-1}+1}-\frac{d(x_{n-1})}{l_{n-1}+1}-\sum\limits_{i=k}^{n-2}\frac{d(x_i)}{l_i+1}=$$$ $$$d(x_{n-1}-\sum\limits_{i=k}^{n-2}\frac{d(x_i)}{l_{i+1}}$$$ Finally we get $$$d(x_k)$$$
In this way, the total sum will be $$$2d(x_k)$$$, $$$2d(x_k)$$$ is bigger than zero, so first equation is bigger then second one, so it isn't optimal to divide and then modify by some prime number $$$q$$$.
Using first and third observation we know we only have to divide by prime number, which aren't divisors of $$$b$$$, and then do modify by prime numbers, which arent't divisors of $$$a$$$.
Using second observation we know that firstly we do dividing then we do modifying.
As we have seen, $$$changing$$$ $$$path$$$ $$$x➔gcd(x,y)➔y$$$ is only one, which fits the requirements, so it is optimal path.
P.S. I think it could be proved much easier :)
Thanks a lot for writing such a detailed explanation! Respect.
Very good.Thanks alot.
Nice problems and a great editorial!
In question C- Circle of Monsters, I used pair to store energy for each monster. After that I used 2 for loops to calculate the minimum bullets required. So, overall time complexity is 2*n, but still I got TLE for Test case 3. I don't know why this happened, am I wrong in calculating complexity or there is some other reason? Code
use scanf and printf
It worked. Thanks! But the constraints were pretty normal. I still can't understand why scanf and printf worked for this problem.
below lines is a bit different in your code, can you try with these? maybe sync_with_stdio() is not same as sync_with_stdio(0) though I haven't checked the docs. you should be always okay with cin, cout without endl
or you can
define endl '\n'Submitted your code again Use the fastio commands properly.
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
Thank you for nice problems and fast editorial, awoo, adedalic, Roms, BledDest!!!
Can anyone explain C more clearl?
have a look to my solution https://codeforces.net/contest/1334/submission/76178087
What I did was calculated the minimum number of bullets required for each position, if started shooting from monster at that position.
How did u do that within given constraints??
My solution was this:
When a monster explodes, there might be some "extra" work that you have to put in to kill the next monster along. This value is
(health of next monster) - (bullets released by previous monster). Where this value is negative, then you have to put in no extra work (the extra bullets you need to shoot is 0). This means that you could use the formulamax(0, a[i] - b[i-1])after you account for the wrapping-around behaviour.Consider the sum, T, of all the extra work that you have to put in for each monster. You can find this by calculating it for every single monster, in O(n), and then adding together all of the values you get.
Then, if you decide to start at a particular monster, this means that the extra work for that monster should not be considered, because the previous monster did not explode. Instead, you need to shoot the same number of bullets as the health of that monster. This means that for any given monster, you can find the number of bullets needed using the formula
(T - (extra work for that monster) + (health of that monster)). We showed above how to quickly work out the extra work for that monster.This means that the solution is O(n) for finding T, and then O(n) for finding how many bullets are needed for each monster, using that value of T.
Thanks a lot for this explanation
Thanks for such explanation
Think it that way: It there where no explosions, we would have to fire one shoot per lifepoint. So, we can earn points by usings explosions.
How much can we earn? The maximum earnings per monster is limited as $$$min(a[i], b[i-1])$$$ This is the power of the explosion, or the total life points of the affected monster, whichever is less.
Since the monsters are in a circle, we can kill on after the other, the explosion damage will be maximum possible on every explosion.
But we have to start somewhere in the circle. The monster where we start does not get any demage by an explosion. As the starting point we use the monster where we would earn the least points, this is the one with minimum $$$min(a[i],b[i-1])$$$
will please explain a little more....how is
maximum earnings per monster is limited as min(a[i],b[i−1])By "earning bullets", we're saying that the previous monster shoots off bullets for free when it explodes, instead of us having to do it. This is very good for us because we want to minimise the number of bullets we shoot, so letting the exploding monsters shoot for us is helpful.
Let's say that the previous monster gives off 5 bullets when it dies, but the next monster has 3 health points. Ordinarily, we would need to shoot 3 bullets to kill the next monster. However, we "earn" those 3 bullets because the previous monster takes care of them for us. Thus, when
b[i-1] > a[i], we "earn"a[i]bullets because we didn't have to shoot them.If the previous monster instead only gives off 1 bullet, then when it dies it reduces the 3 health points of the next monster to just 2 health points. We would have needed to shoot 3 bullets to kill the next monster, but now we only need to shoot 2 bullets. Thus, the previous monster has "earned" us 1 bullet by exploding. Thus, when
b[i-1] < a[i], we "earn"b[i-1]bullets.This means that the formula
min(a[i], b[i-1])is just telling us the bullets that we don't have to shoot if we rely on the previous monster exploding instead.You might also choose to think of this problem as how many bullets do you still have to shoot despite all the help from monsters exploding. And this is very similar:
max(0, a[i] - b[i - 1])great explanation....thanks
I think my solution is pretty neat used a rolling function to brute force for all rotations
Why I got tle in this https://codeforces.net/contest/1334/submission/76133446 It is nlog n only!!!
Use ArrayList instead of long[]
Maybe problem in not fast Java io.
Arrays.sort() can get up to n^4 time in weird cases like for nearly sorted raw type arrays (e.g long[]). To combat this, use Long[] or an ArrayList instead when you plan to sort the contents of a long[] array. I guarantee this change will fix your solution.
I faced this exact same problem, and only after the contest did I switch the long[] to a Long[] and finally pass all test cases.
Can someone explain why were there so many successful hacks on problem B that result in the program getting Time Limit Exceeded? How do the hacks work? Is it because of a flaw in the programming language's sort function?
Also, are the weak tests for problem A intentional?
Hi, I did many of the hacks for B. You are correct. In java, sorting an array of primitives uses quicksort. This can be exploited by creating an anti-quicksort hack to force the sort to run in O(N^2).
You can simplify the solution of problem E by using the fact that the graph is somewhat self isomorphic. So if you want to count the paths from $$$x$$$ to $$$y$$$ you can also count the paths from $$$\frac{x}{\gcd(x,y)}$$$ to $$$\frac{y}{\gcd(x,y)}$$$. Each shortest path will now go through $$$1$$$, therefore you only need the number of paths from $$$1$$$ to $$$d$$$ for each divisor $$$d$$$ of $$$D$$$. This can be calculated before with a simple do. My implementation: 76229493
Cool!!!)
Really liked problem D!
Can anyone explain problem D??!
First try to write the whole lexicographically smallest cycle of the whole graph.
For simplicity I will take a complete graph of size 4: ( the graph below should be bi-directional )
The lexicographically smallest cycle of this graph is:
1 2 1 3 1 4 2 3 2 4 3 4 1
As you can see, there's a pattern here ( 1 2 1 3 1 4 ) ( 2 3 2 4 ) ( 3 4 ) ( 1 ) which can be modeled by this for loop:
Still this is O(n^2), to make it O(n) we need the element close enauph to l and complete the pattern and write the element between l and r, to so do we can simplify the search using this observation: in the pattern the first group starts with 1 and it's of size 2*(n-1), the second group starts with 2 and it's of size 2*(n-2) and so on, we can use this fact to loop through i and find and i such that 2*(n-i) is closest to l , then just print the elements between l and r.( don't forgot the 1 at the end).
Great explanation. Thanks a lot!
Suppose n = 5. for now forget about l and r. Then the lexicographically smallest list will be:
1 2 1 3 1 4 1 5 (1-5)
2 3 2 4 2 5 (2-5)
3 4 3 5 (3-5)
4 5 (4-5)
1.
And what if n = 6? If you guess it right, the list will be:
1 2 1 3 1 4 1 5 1 6 (1-6)
2 3 2 4 2 5 2 6 (2-6)
3 4 3 5 3 6 (3-6)
4 5 4 6 (4-6)
5 6 (5-6)
1
Try it with some other graph with different number of vertices. Keep sum of every list above in a prefix array. From there it will be easy to determine where l starts and where r ends.
I got that too during practice. But the ques is, we can't store anything because of the large value of l and r, how can we know what element we would get in specific index without storing, I can't get any mathemetical formula
Look at my example above. When n = 5, length of the first list is 8. Sec list is 6, third is 4 and so on. We can store only the length of each sequence in an array. We don't need to store the whole sequencs. Got it now? Think for sometime about what I just said.
Oh thanks vai, got it.
Can someone please explain the solution of D? I am not able to understand editorial clearly..
First of all lets try to construct the lexographically minimum cycle in the graph:
We have to choose a starting node, we will choose node 1 otherwise any other other as starting node makes the cycle lexographically greater than {1 followed by some other nodes}.
For example : {3 followed by some other nodes} > {1 followed by some other nodes}.
Now we have chosen the starting node as node 1. Where should we go now? Given a complete graph you could go to any other node, so we choose 2.
Because again {1 follow by 2 followed by some other nodes} is less than any other possibility.
now we have 1->2, now where? Again choose 1(for similar reasons). so we have 1->2->1.
now we are back at node 1 but now we can not choose to go to node 2 again(edge 1->2 is already traversed once). So we are forced to go to some node j ( j > 2).
Again for similar reasons explained above, you will choose to go to node 3.
1->2->1->3. Where now? from 3 you may go to any other node.
So again go to 1 : 1->2->1->3->1 So if you see the pattern now, then we have :
1->2->1->3->1 ... 1->n-1->1->n Now where? If I go back to 1 then I am trapped because I have already used every outward edge from 1. So I am forced to go to node 2 instead of 1.
1->2->1->3->1 ... 1->n-1->1->n->2->3->2->4->2 ... 2->n-1->2->n
So we get the lexographically smallest cycle as below : {1->2->1->3->1 ... 1->n-1->1}->n->{2->3->2->4->2 ... 2->n-1->2}->n->{3->4->3...->3->n-1->3}->n.....n->{n-1}->n->1.
The thing inside the braces(call it Bi) is simply {i->i+1->i->i+2 and so on} and after that back to node n.
Once done we complete the cycle by traversing the edge n->1.
Now choose in which brace from 1 to N-1 your L falls and generate that brace content to print. Ofcourse L to R may span over more than one braces or no braces at all(last two or L falling right at the end of some brace).
Hope this helps :)
Thanks it really helped :)
Please , have a look at my solution : https://codeforces.net/contest/1334/submission/76259835 Can anyone please help me out to get why I'm getting wrong answer . Thank You
I didn't understand what was your idea, but I think you should have a look at my code. Idea: lets sort our array, if at some position i we have that a[i] + a[i + 1] + ... + a[n — 2] + a[n — 1] >= x * (n — i) then (a[i] + a[i + 1] + ... + a[n — 2] + a[n — 1]) / (n — i) >= x. Thats why all this people are reach. Thats why we want to maximize n — i (minimize i) and loop goes while all people at suffix are reach.
Thank you for replying me back . I got your answer but I need to know the test case where my code fails to pass the test case . This code https://codeforces.net/contest/1334/submission/76145656 is almost same as mine but got the AC verdict . Please somebody help me out by finding such a case where i got stuck .
Thank You
Try this:
Thank You very much . hope u will succeed in your life . But how could you arrive at this test case . Is there a way to find out such type of test cases in code forces website or just by hit and trial and practice .
Thank You
Just practice to find errors in code.
E was not only an interesting problem But also a fresh one ! Enjoyed it.
Cleaner solution to problem F, without any kind of data structure:
You can add $$$0$$$ and $$$n+1$$$ to the beginning and end of the lists $$$a$$$ and $$$b$$$ to complete them. Transform the sequence $$$a_i$$$ into a simpler sequence to solve the problem. If $$$a_i = b_j$$$, then you rewrite $$$a_i := 2j$$$. However, if $$$b_j < a_i < b_{j+1}$$$, rewrite $$$a_i := 2j+1$$$ (throughout the article
:=means assign).Thanks to this, we need to form a increasing (two by two) sequence of numbers from $$$a$$$ starting at $$$0$$$ and ending at $$$2m$$$. To do so, we will use the following idea:
Now. Let's put it into a dp:
In general:
dp(i) := dp(x) + prefix-sum of values 2j in [0, i) + prefix-sum of values 2j+1 on [0, i) + negatives-sum on (x,i), where $$$x$$$ is the last position $$$a_x = 2j-2$$$.If we forced to choose the position $$$i$$$. To take into account the previos positions:
dp(i) := min(dp(i), dp(x) + negatives-sum on (x, i], where $$$x$$$ is the previous position with $$$a_x = 2j$$$.Using lower_bound to get the prefix sums and the indices $$$x$$$ makes the algorithm run in $$$\mathcal{O}(n \log n)$$$. However, using an array of size $$$n$$$ to compress the sequence (given that $$$b$$$ is sorted) and to keep the last position of each element when traversing from $$$i = 0$$$ to $$$i = n$$$ we can do it in $$$\mathcal{O}(n)$$$.
I wrote the $$$n \log n$$$ solution shortly after the contest: https://codeforces.net/contest/1334/submission/76218976
Do you mean you can write an $$$O(n)$$$ solution or only a part of it?
I modified a little bit my code to show how it's done in $$$\mathcal{O}(n)$$$.
https://codeforces.net/contest/1334/submission/76272882
Oh, sure, I forgot that all the values are in $$$[1, n]$$$. Nice solution btw.
Thanks. I resubmitted with a code a bit more simpler.
Here is my $$$O(n)$$$ solution for problem E: https://codeforces.net/contest/1334/submission/76272574
I count negative sums separately and keep track of cost to remove all positive $$$a_i$$$ for each range $$$(b_{j-1}, b_j]$$$ from beginning of array $$$a$$$ to current position $$$i$$$.
I just submitted my $$$O(n)$$$ version 76395088, which is simpler than edsa's. However, I found that yours is the simplest one. :)
Very late but could you please explain your approach, I got lost from the first step(not able to understand why use lb)
lb means lower_bound. lb helps to find index of item in B by its value. i.e for each integer x from 0 to m, lb[x] = index of first item in B which is >= x. or lb[x] = m if there is no such item. i.e all items in B are strictly less than x
when we iterate over A, lb helps us to check quickly if A[i] exists in B.
also for any A[i] it helps to identify range (pair of
B[idx - 1].. B[idx], that covers A[i], i.e.B[bidx - 1] < A[i] <= B[bidx]).ccost[idx]keeps cost to remove all items with positive p[j] from current prefix of Aa[0]..a[i]such thatB[bidx - 1] < A[j] <= B[bidx] (0 <= j <= i);if on next steps we find A[i] that exists in B, we need to consider case to remove all items from prefix of A that belongs to the same range as A[i].
ccost[bidx] - p[i] + dp[bidx]— this is cost to make A[i] an item that survives function F. (an item which is greater of all the items in the prefix before it)Cool explanation. Can you take a look at my code.I used dp[i][j] as minimum number of coins required to generate first j elements of array B using only the first i elements of A. Transitions are quiet straight forward. If next element of A is the next required element of B and I am considering that element dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]). If I dont consider the next element ie I want to delete it,dp[i][j+1]=min(dp[i][j+1],dp[i][j]+a[j]) My answer would be dp[m][n]. I dont understand where I am going wrong. https://codeforces.net/contest/1334/submission/76300349 Thanks in advance:)
Will that fit into the time limit?
1334C — Circle of Monsters BledDest does this problem can be solved using dynamic programming if we store that how much bullets it will take to destroy all monster start from first and when we go further remove the bullets used by previous one and reduce the damage caused the previous monster on blast and count bullets for each of this individually and minimum of it is answer.
Why to use missile when job can be done with knife?
Can someone explain why C has to be done in order? Like why is it most efficient to shoot the monsters in the order that they are standing in?
If we remove the monster at a position i before removing the monster at position i-1 then we won't be able to utilize the explosion of the monster at position i-1. And since, we want to maximize the utilisation of explosions so as to reduce the number of bullets used, we remove the monsters in the order they are standing. In this way, only the explosion of the monster removed last will be wasted.
Nice contest!
btw in problem E, why is “You can remove them in any order because the length of the path is always the same” true?
Every vertex of the graph stands for a list of primefactors. Each edge removes or adds one such primefactor depending on direction of traversal.
So, to find the path from one list of primefactor to another one, we need to remove all primefactors which are in the first list but not in the second, and add all primefactors wich are in the second list but not in the first one.
The order of removals and addings simply does not matter.
thx:)
Can anyone explain why I am getting TLE for this solution https://codeforces.net/contest/1334/submission/76287771 even for O(n) Complexity. The Problem is https://codeforces.net/contest/1334/problem/C (C. Circle of Monsters)
Resubmit of your code: https://codeforces.net/contest/1334/submission/76297548
I had the same problem with my solution. I changed all cin to scanf, cout to print. It helped to improve execution time from TLE to 280ms. oh, "ios_base::sync_with_stdio(0);" at the start of main also helped
I would like to know the code of solving f with O (nm) method
Who can show me code .
Thanks
It looks that I have had a simpler solution for the problem G. I write it down here.
For each $$$d$$$, compute $$$\sum_{i = 0}^{n - 1} (t_{d + i} - s_i) (t_{d + i} - p(s_i)) = \sum_{i = 0}^{n - 1} t_{d + i}^2 + \sum_{i = 0}^{n - 1} s_i p(s_i) - \sum_{i = 0}^{n - 1} t_{d + i}(s_i + p(s_i))$$$, where the last term can be done with NNT.
Suppose that we do the arithmetic under a prime field of order $$$p$$$. If we randomly sample $$$26$$$ elements in $$$F_p$$$ to be a, b, ..., z, the computed sum will be zero with probability less than $$$\frac{1}{p}$$$ if not all $$$(t_{d + i} - s_i) (t_{d + i} - p(s_i)) = 0$$$.
Is there a simpler explanation for problem C?
There is one monster you need to shoot first. This monster will not be affected by the explosion of the previous monster, all other monsters will be affected by the explosion of the previous ones. So you just calculate the monster, for which the explosion will save you the least amount of shots and then simulate the shooting starting from this monster.
Hi, I am unable to understand the problem c solution. Can anyone please help me understand it.
A part of proof for problem E
We will represent numbers as tuple.
$$$x=(a,b,c,d,...)$$$ means $$$x=2^a.3^b.5^c.7^d....$$$.
Let $$$(a,b,c,d,e,...)$$$ and $$$(a',b',c',d',e',...)$$$ be the tuple representations of x and y respectively.
In one step we can perform two types of operations:
(1) $$$(a,b,c,d,e,...)$$$ becomes $$$(a+1,b,c,d,e,...)$$$
(exactly one number among a,b,c,... can be increased by 1, for the sake of clarity a is increased by 1)
from now on we will call it increasing operation.
(2) $$$(a,b,c,d,e,...)$$$ becomes $$$(a-1,b,c,d,e,...)$$$ from now on we will call it decreasing operation.
The cost of both operations is $$$(b+1)(c+1)(d+1)(e+1)...$$$
Our goal is to go from $$$(a,b,c,d,e,...)$$$ to $$$(a',b',c',d',e',...)$$$ using such operations
Some pairs say $$$a,a'$$$ satisfy $$$a<a'$$$ while some others say $$$b,b'$$$ satisfy $$$b>b'$$$ and while some others say $$$c,c'$$$ satisfy $$$c=c'$$$.
Claim 1:
No operations must be performed on pairs of type $$$c,c'$$$ such that $$$c=c'$$$.
Proof:
If there are operations performed on $$$c$$$ removing all such operations does not increase the cost.
Claim 2:
All decreasing operations must be performed before increasing operations.
Proof:
Assume on the contradiction that a optimal way to go to y from x performs a decreasing operation after increasing operation.
For concreteness lets assume
$$$(a,b,c,d,e,...)\rightarrow (a+1,b,c,d,e,...) \rightarrow (a+1,b-1,c,d,e,...)$$$
it's cost is $$$(b+1)(c+1)(d+1)(e+1)... + (a+1)(c+1)(d+1)(e+1)...$$$
swapping both operations gives
$$$(a,b,c,d,e,...)\rightarrow (a,b-1,c,d,e,...) \rightarrow (a+1,b-1,c,d,e,...)$$$
it's cost is $$$(a+1)(c+1)(d+1)(e+1)... + b(c+1)(d+1)(e+1)...$$$ and it's less when compared to the above cost. So the assumed order of operations is not optimal.
(Notice that final state in both cases is $$$(a+1,b-1,c,d,e,...)$$$)
Claim 3:
Increasing operations can be performed in any order
Proof:
For concreteness assume two adjacent increasing operations to be
$$$(a,b,c,d,e,...)\rightarrow (a+1,b,c,d,e,...) \rightarrow (a+1,b+1,c,d,e,...)$$$
it's cost is $$$(b+1)(c+1)(d+1)(e+1)... + (a+2)(c+1)(d+1)(e+1)...$$$ which is equal to
$$$(a+b+3)(c+1)(d+1)(e+1)...$$$
swapping the two operations gives
$$$(a,b,c,d,e,...)\rightarrow (a,b+1,c,d,e,...) \rightarrow (a+1,b+1,c,d,e,...)$$$
and it's cost is $$$(a+1)(c+1)(d+1)(e+1)... + (b+2)(c+1)(d+1)(e+1)...$$$ which is again equal to
$$$(a+b+3)(c+1)(d+1)(e+1)...$$$.
Claim 4:
Decreasing operations can be performed in any order
Proof:
Goes on the same lines as above.
Putting all these claims together we can say that we must first perform all decreasing operations and they can be performed in any order and after performing all decreasing operations we reach $$$gcd(x,y)$$$ and then we must perform all increasing operations and they can be performed in any order.
Note:
(1) This proof is not complete.
(2) Please correct me if I am wrong and please comment if you have any queries with regard to this proof.
Good explanation brother. You deserve more upvotes.
https://codeforces.net/contest/1334/submission/76169596 can someone tell me the problem in my code for question C Circle of Monster I am trying to iterate over all the starting positions to kill the monster and finding the minimum bullets used.
Line 24
i = n-(k+in);
must be i = k+in-n;
even then your solution will exceed time limit
Does anyone solved F using Persistence Segment trees? I am getting MLE. BledDest awoo is it intentional? If not can you please suggest me how to optimize with the memory? My Submission Link
It is possible to solve it using just Segment trees since b1...bn is in increasing order.
shouldn't a 26 * (|s|+|t|)* (log((|s|+|t|)) work for G
my approach was for each character i was creating a bit array for both t and s also i was considering the mapping of the indexes's given to be 1 in the bit array of t
for example if 1 is mapped to 20, then I put one int all those indexes that was having characters as a and t. and then performing a fft with a bit array of s reversed (using only a's for masking).
similarly for all characters. and then adding all the results of fft's ,if the index has value == size(s) then that index matches the substring.
please correct me where i am wrong. Or this approach shouldn't pass this constraint?
@pikmike @BledDest
For $$$F.$$$ Why no-one is talking about easy sgmt tree soln. . Editorial for F is tough to understand . lazy tree updates from 1 to x and another from x to m (if<0) , and updating dp as min(dpi,dp_i-1+p_i-1) . PLEASE tell me if its correct or not . As i have not coded yet!!
I got WA on C due to using LONG_MAX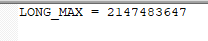 Why LONG_MAX is same as INT_MAX. I couldn't find answer on google...!
Why LONG_MAX is same as INT_MAX. I couldn't find answer on google...!
Because 'long int' is same as 'int' in 32-bit compilers and CF has a 32-bit compiler. Check this out. You can use 'long long int' for 64-bit integers.
i am getting wrong ans in D can anyone plz check my solution https://codeforces.net/contest/1334/submission/79674936
can someone explain why i m gettibg a tle for question 3 at test 3 in o(n). https://codeforces.net/contest/1334/submission/85927573
change endl to \n and add fast i/o
check this out https://codeforces.net/contest/1334/submission/89154507