What are your solutions?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 13:48:49 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Here is my solution for
Expogobut it is givingWA. Any suggestions why I am getting WA?You swapped flag1 and flag2.
worst mistake I had ever done. Cost me everything. I have given this question all time.
vineetjai, For Question 1 from CodeJam Round 1A, how did you learn the bitwise logic behind the question? Did you obtain this from practice?
just used the logic that the steps are in powers of 2. yes it was a little bit tricky but I think key observation is that you have to use every powers of 2 exactly once. also, you have to practice bit manipulation question for this.
Can you explain your answer ?
https://codeforces.net/blog/entry/76281?#comment-607555 this is the nearly the same logic I had used.
Haven't solved any. But interested to know — How would you compare the difficulty level of the first, second and third problems in GCJ to the code forces Div2/Div1 problems? I can solve Div2 — C, D (at best). Never tried an E. But GCJ 1st problem seems harder than Div2-C. How would you practice on Codeforces for a GCJ Round 1?
this round was much tougher than previous round 1's . p1 > div2d p2 > div2e p3 > div2f or more.
I think P2 isn't harder than Div2E difficulty. For me P2 was easier than P1.
as u say.. but i felt harder than old round 1. I have solved all round 1 problems from 2008 to 2017 and this problem set was harder that old ones.
P2 was surely easier than P1, even for me, but implementing a binary search and that too during a round was so frustrating, I ditched it finally!
This is why you should do modular programming. :)
I'd say today's A is Div1 B/C, and today's B is Div1 A/B.
What about C?
Lmao, how to solve A?
I tried it for over an hour, then finally moved on to B (which I think is more straightforward).
Let $$$N$$$, $$$S$$$, $$$E$$$ and $$$W$$$ be masks representing the moves in corresponding directions.
$$$N-S = Y$$$
$$$E-W = X$$$
Lets fix number of moves K Then,
$$$N+S+E+W = 2^K-1$$$
From above equations we can solve for, $$$N+E$$$, $$$S+W$$$ and $$$N+W$$$ lets say $$$a$$$, $$$b$$$ and $$$c$$$.
Since, each bit can be present in only one of them, we get
$$$N=a$$$ & $$$c$$$
$$$E=a - N$$$
$$$W=c-N$$$
$$$S=b-W$$$
Now, we can just check if the solution is valid.
hitman623 where can i find such type of problems for practice ?
:O
Also, congrats for country rank 1
I have some doubts. What you mean by masks here ? and how n + s + e + w = 2^k — 1.
The bits which are ON in mask $$$N$$$ are the moves in the North direction. When we fix number of moves, each move/bit should be present in exactly one of $$$N$$$, $$$S$$$, $$$E$$$ and $$$W$$$ therefore they sum up to $$$2^K-1$$$.
Could you further explain your intuition behind: N = a&c
This makes sense. Thank you.
This is the solution i was seeking. Thanks a lot.
Find mininal T such that 1 + 2 + 4 + 8 + ... + T >= abs(X) + abs(Y). Now for each of {1, 2, 4, 8, ..., T} you can uniquely determine if it should be negated. Now you have a vector of <= 31 numbers. You should choose a subset with sum equal to x (other numbers will have sum y). It is done with meet in the middle.
Thanks for describing your solution idea. How do you determine the sign of each of {1, 2, 4, 8, ..., T}?
You need to subtract s = (sum — (abs(x) + abs(y))) from the sum (sum = LHS).
Negative numbers are just the binary representation of the s/2 (if s is divisible by 2 (else "IMPOSSIBLE"), which also essentially means x and y should have different parities).
Does sum = 1 + 2 + 4 + 8 + ... + T in your notation?
yes
I'm really sorry for the stupid doubt, but can you explain the meet in the middle part? I wasn't able to think that.
$$$T$$$ is for sure smaller than $$$2^{40}$$$. As the sign can be determined for each bit, looking at the sum $$$x + y$$$, there are $$$2^{\log T} = T$$$ combinations. This is too much, so let's start off by calculating all the possible values of $$$x'$$$ (so the first half of the $$$x$$$) looking just at first $$$\frac{\log T}{2}$$$ bits. We move to the second part, and for each $$$x' '$$$ (second half of $$$x$$$) we check if such $$$x'$$$ exists that $$$x' + x' ' = x$$$.
We can do it greedily instead of meet in the middle.
We can get a valid solution if $$$1 + 2 + 4 + \dots + T \geq |x| + |y|$$$ and $$$x \not\equiv y$$$. Let's decide what do we do with $$$T$$$. We want to get such $$$(x', y')$$$ that $$$1 + 2 + 4 + \dots + T - T \geq |x'| + |y'|$$$. Assume that $$$|x| > |y|$$$. A valid pair $$$(x', y')$$$ is $$$(x \pm T, y)$$$, minimizing the absolute value of $$$x \pm T$$$. The pair is valid, so the rest of solution exists.
Another way to do it is to think about what do we do with $$$1$$$, not $$$T$$$. Since exactly one of $$$x$$$ and $$$y$$$ is odd, we need to increase/decrease that number by $$$1$$$. Now $$$x$$$ and $$$y$$$ are both even, so we divide everything by 2 and continue with the next bit.
Try to reproduce the sequence in reverse direction. On each step, check what coordinate has larger absolute value, and make a shift towards the origin along that axis.
Suppose we are at step $$$2^k$$$, with current coordinates being $$$x$$$ and $$$y$$$.
There are some cases:
I solved it using some visualization. I found the points reachable for every possible string for Len =1,2,3 and then it just followed a pattern. Every point reachable by Len=w will be reachable by Len= z where z > w.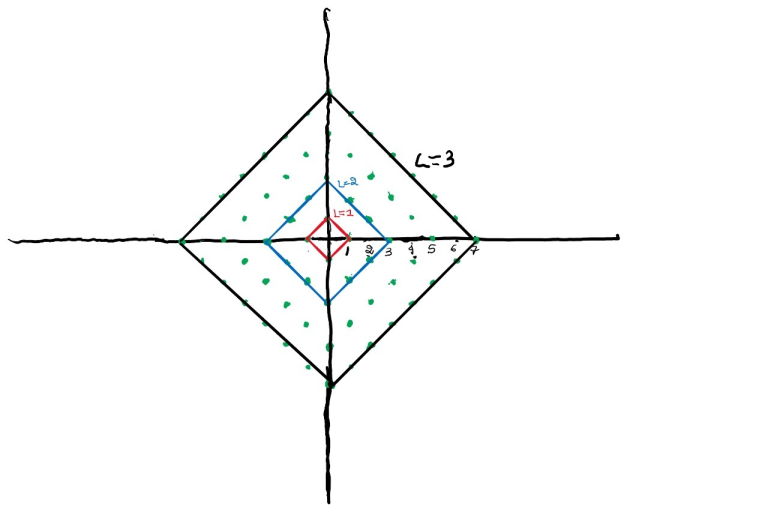
And if abs(x) + abs(y) = even, then answer is impossible. After this we only need to generate the path. Here is the visualization:
What do you mean by len?
Len is the length of the string, For example if we are considering Len = 1 then the possible strings are N, W, S, E. And for these strings the integer points on the red square are reachable.
For Len = 2. Possible strings are NN, NW, NE, NS ... and so on. And for Len =2, The integer points on the blue square and on the red square are reachable. For Len = 3 all the points on the curve |x| + |y| <= K, where K is odd and K <= (2^3-1) are reachable.
So in general for Len = n, all the points on the curve |x| + |y| <= P where P is odd and P <= (2^n-1) are reachable.
Well, I ran a dfs basically for every index (1<<index) has to present in any one of the directions if at any point u find that N-S == Y && E-W == X print the answer. I got AC for test set 1 and 2 but failed for 3 bcoz of the costly time complexity :(
Hard problems.
A looks like this one: ARC103D. I was suprpised to see it as the first one.
B can be solved by finding any point in the circle and then doing 4 binary searches.
Any ideas to solve C?
In C, I couldn't come up with a tc where just coming from back and maintaining sorted order from back will fail. does anyone know the testcase?
Let's name continuous sequence of cards with same rank as a group. First obvious observation: you shouldn't divide group.
Let's name group which contains all the suits as complete one. Otherwise it is incomplete.
The main idea is that if you have two incomplete groups on the top of the deck — you should place them (select as pile A) between next two cards with same ranks as cards in groups(*)(**). Otherwise, there remains only one incomplete group, which can be completed in a single operation.
(*) — Such cards will always exist because groups aren't complete. Also, it's guaranteed that this cards will be consequent because described solution will keep relative order of card ranks.
(**) — In such a way you will add one card to both groups in single operation and this is the best we can achieve with described type of operation.
Problem 2 "Blindfolded Bullseye" gave TLE( in the 3rd hidden test set) in many solutions including me.
Please someone tell the reason why?
problem link: https://codingcompetitions.withgoogle.com/codejam/round/000000000019fef2/00000000002d5b63 My sol link :https://codingcompetitions.withgoogle.com/codejam/submissions/000000000019fef2/bWVodWxfMDI
Here is my link to my code of B. It's giving TLE, I am not able to figure out why. I am finding the first hit point and then applying 4 binary search. Any suggestions on where I am doing wrong?
I am doing the same and have the same doubt :/
[deleted] do_good_ is right
You were also technically right that it is a mistake, but the odds of hitting the center are too small. Since statement says the position is pregenerated, there's no issue of adaptive grader testing if you handle the corner case correctly.
actually you are getting TLE bcoz you are taking cin >> x >> y for every test case in solve() function. just use it once. i tried it and it is giving WA for ur code.
I spend most of time with TLE due to same issue.
u need to input a and b only one time
I spent the entire time trying to solve problem A, but ended up getting WA on 1 of the test sets. Later I realized that B was a little bit easier than A, but it was too late. Any advice guys on how to attempt problems in competitions where relative difficulty of problems is not mentioned( ex : in codeforces, we can easily discover that problems are given in increasing order of difficulties) ?
Nobody seemed to describe the easiest solution to A (at least for me). If x and y are both even or both odd we clearly can't get to the goal (except if x=y=0). If x is odd we branch to reduced problems for ((x+1)/2, y/2) and ((x-1)/2, y/2), similarly for the case when y is odd. It can be proven this backtrack has O(log(range)) nodes, since values of x differ by one only, so one of them will be cut out by parity check, so basically our move is uniquely determined at every level (except for the case when we can go to (0, 0), but then we want to go there no matter what).
Same solution here.
I was looking for something like this, thanks a lot!
Is there a way to modify interactive_runner.py so that the interaction between the two programs is outputted somewhere?
This is a modification I did to last year runner. I think the runner changed this year, so beware not to use that code, but try to adapt that to the new runner. Probably I'll do it before Round 2 if anybody had.
I'm getting
WA - -forExpogoon submission. Here is the code run on the first 80 test-cases. IDK which one I'm getting WA on. Can anyone suggest which one I'm getting WA on?my submission This is first problem of GCJ 1B, Can anyone help me why this is accepted instead of giving TLE, I think when tt(in my code line no. 84) is large, it should give TLE.
Your loop contains simple instructions, and you can thank google's 10+ seconds TL policy for the rest.
The 20 seconds time limit should easily allow you to run the loop 1e9 times.
I wonder what the logic is behind your solution?
Find mininal T such that 1 + 2 + 4 + 8 + ... + T >= abs(X) + abs(Y).
Here sum is 1 + 2 + 4 + 8 + ... + T. So we have extra move is (sum-abs(X)-abs(Y)), let we call it as tt. Now p=tt/2 moves will be in the negative direction. And out of this p moves, I assume that f1 moves will be in negative direction of X and f2=p-f1 moves will be in the negative direction of Y. So I run a loop for f1 from 0 to p.
Now,for any f1 and f2 answer is possible only when XOR of (f1,f2,X+f1,Y+f2) is sum.
Another solution for A, which was straightforward for me (probably not as simple as Swistakk's solution).
Iterate over the bits of both $$$x$$$ and $$$y$$$ from right to left. Let us say we're on the $$$i$$$'th bit from the right. If both the bits are equal, it is impossible.
Otherwise, check if the $$$i + 1$$$'th bits of the two numbers are equal or not (the bits to the left of our current bits). If they are not, subtract the power of two (by setting appropriate directions) from either $$$x$$$ or $$$y$$$ based on which number's $$$i$$$'th bit is set. If they are equal, add the power of two to either $$$x$$$ or $$$y$$$, again based on which number's $$$i$$$'th bit is set. If both $$$x == 0$$$ and $$$y == 0$$$, break the loop.
This works because if the $$$i$$$'th bits of the two numbers are equal and we've used up all the powers of two for $$$2^k$$$ for $$$k < i$$$, it is impossible. Otherwise, we can either subtract the power of 2, or add it so that the next bit (to the left) which is 0 gets set, and all the bits to the right become 0.
(When I say subtract and add, I mean setting the directions appropriately so that the $$$x$$$ or $$$y$$$ value either increases or decreases; we get our answer when both the values are 0, i.e, we are at our target)
I used the same logic.
How did the people who solved C arrived at the solution? It will be very helpful to me and others to know the thinking process required in this type of problems.
Did anyone solve it by simulation + Observation on small cases?
On the beginning I noted that $$$\lceil \frac{(s-1)r}{2} \rceil$$$ is kind of an obvious lower bound, but didnt have an idea how to construct it, so I was dubious about it being correct answer. Then I wrote simple exponential bruteforce BFS on all permutations, because I thought it would be too hard for me to guess the pattern quickly. Fortunately, solutions I got from it were very heplful and helped me notice the patterns, but even with it, I needed to consider a lot of small cases by hand to get the hang of it and answer turned out to be equal to that lower bound indeed. In total that was pretty hard problem for me, took me more than hour. I am often against writing bruteforces to notice patterns if thinking could be used instead (it is often the case that Radewoosh tells me and Marek that we are stupid because we have not written backtrack for some small cases even though the problem was so simple we managed to get its full understanding within one minute), but everything has its own balance — if problem seems hard to you to then it may be a good idea. I am sure many people solved it without help of bruteforce though, it was doable as well. Probably the best line of attack without writing bruteforce was investigating the lower bound and targeting it directly by inspecting what kind of move we need to make to not make it worse (<=> always creating two pairs of adjacent numbers that will stand next to each other in sorted sequence).
In problem A I tried 0 to 32 walks scenarios, and in each scenario I chose from the biggest step to the smallest step while minimizing the manhattan distance between current position and the goal greedily. However I just can't explain why did it works, pls help.
https://codeforces.net/blog/entry/76281?#comment-607467
Thanks.
In problem B. Since, the x-axis (y = 0) and the y-axis (x = 0) will definitely touch or intersect the circle. So using binary search, I calculated the points of intersection. Now we have two perpendicular chords (or tangents). We can easily find the centre using their mid-points. To get rid of errors I'm also checking some points which are in the neighbourhood of our expected answer.
But I'm getting WA :(
Can anyone please tell me how this is wrong?
How have you applied binary search?
In order to use binary search, you need to find a point laying inside the circle or on the border at first.
Can you once go through my code? Link
Problem A Explanation with code if anyone is interested Here
IF anyone need Problem B explanation and code Here