Idea: BledDest
Tutorial
Tutorial is loading...
Solution (pikmike)
t = int(input())
for _ in range(t):
a, b, c, d = map(int, input().split())
if b >= a:
print(b)
continue
if c <= d:
print(-1)
continue
a -= b
dif = c - d
print(b + (a + dif - 1) // dif * c)
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
char buf[200043];
int main()
{
int t;
scanf("%d", &t);
for(int i = 0; i < t; i++)
{
scanf("%s", buf);
string s = buf;
int ans = int(1e9);
int n = s.size();
vector<pair<char, int> > c;
for(auto x : s)
{
if(c.empty() || c.back().first != x)
c.push_back(make_pair(x, 1));
else
c.back().second++;
}
int m = c.size();
for(int i = 1; i < m - 1; i++)
if(c[i - 1].first != c[i + 1].first)
ans = min(ans, c[i].second + 2);
if(ans > n)
ans = 0;
printf("%d\n", ans);
}
}
1354C1 - Simple Polygon Embedding
Idea: adedalic
Tutorial
Tutorial is loading...
1354C2 - Not So Simple Polygon Embedding
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
import kotlin.math.*
fun main() {
val PI = acos(-1.0)
val T = readLine()!!.toInt()
for (tc in 1..T) {
val n = readLine()!!.toInt()
var ans : Double
if (n % 2 == 0) {
ans = 1.0 / tan(PI / (2 * n))
} else {
ans = cos(PI / (4 * n)) / sin(PI / (2 * n))
}
println("%.9f".format(ans))
}
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (BledDest)
#include<bits/stdc++.h>
using namespace std;
int n, q;
vector<int> a, k;
int count_le(int x)
{
int cnt = 0;
for(auto y : a)
if(y <= x)
cnt++;
for(auto y : k)
{
if(y > 0 && y <= x)
cnt++;
if(y < 0 && abs(y) <= cnt)
cnt--;
}
return cnt;
}
int main()
{
scanf("%d %d", &n, &q);
a.resize(n);
k.resize(q);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
for(int i = 0; i < q; i++)
scanf("%d", &k[i]);
if(count_le(int(1e9)) == 0)
{
puts("0");
return 0;
}
int lf = 0;
int rg = int(1e6) + 1;
while(rg - lf > 1)
{
int mid = (lf + rg) / 2;
if(count_le(mid) > 0)
rg = mid;
else
lf = mid;
}
printf("%d\n", rg);
return 0;
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution (pikmike)
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define mp make_pair
#define pb push_back
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define forn(i, n) for(int i = 0; i < int(n); i++)
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template <class A, class B> ostream& operator << (ostream& out, const pair<A, B> &a) {
return out << "(" << a.x << ", " << a.y << ")";
}
template <class A> ostream& operator << (ostream& out, const vector<A> &v) {
out << "[";
forn(i, sz(v)) {
if(i) out << ", ";
out << v[i];
}
return out << "]";
}
mt19937 rnd(time(NULL));
const int INF = int(1e9);
const li INF64 = li(1e18);
const int MOD = int(1e9) + 7;
const ld EPS = 1e-9;
const ld PI = acos(-1.0);
const int N = 5000 + 7;
int n, m;
int a[3];
vector<int> g[N];
bool read () {
if (scanf("%d%d", &n, &m) != 2)
return false;
forn(i, 3) scanf("%d", &a[i]);
forn(i, n)
g[i].clear();
forn(i, m){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].pb(u);
g[u].pb(v);
}
return true;
}
int tot0, tot1;
int clr[N];
vector<vector<int>> vts[2];
bool ok;
void dfs(int v){
tot0 += clr[v] == 0;
tot1 += clr[v] == 1;
vts[clr[v]].back().pb(v);
for (auto u : g[v]){
if (clr[u] == -1){
clr[u] = clr[v] ^ 1;
dfs(u);
}
else if (clr[u] == clr[v]){
ok = false;
}
}
}
int dp[N][N];
int res[N];
void solve() {
vector<pt> siz;
memset(clr, -1, sizeof(clr));
vts[0].clear();
vts[1].clear();
forn(i, n) if (clr[i] == -1){
tot0 = tot1 = 0;
clr[i] = 0;
ok = true;
vts[0].pb(vector<int>());
vts[1].pb(vector<int>());
dfs(i);
if (!ok){
puts("NO");
return;
}
siz.pb(mp(tot0, tot1));
}
memset(dp, -1, sizeof(dp));
dp[0][0] = 0;
forn(i, sz(siz)) forn(j, N) if (dp[i][j] != -1){
dp[i + 1][j + siz[i].x] = 0;
dp[i + 1][j + siz[i].y] = 1;
}
if (dp[sz(siz)][a[1]] == -1){
puts("NO");
return;
}
puts("YES");
memset(res, -1, sizeof(res));
int cur = a[1];
for (int i = sz(siz); i > 0; --i){
for (auto it : vts[dp[i][cur]][i - 1])
res[it] = 2;
cur -= sz(vts[dp[i][cur]][i - 1]);
}
forn(i, n) if (res[i] == -1){
if (a[0] > 0){
res[i] = 1;
--a[0];
}
else{
res[i] = 3;
--a[2];
}
}
forn(i, n) printf("%d", res[i]);
puts("");
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
int tt = clock();
#endif
cerr.precision(15);
cout.precision(15);
cerr << fixed;
cout << fixed;
while(read()) {
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
}
Idea: BledDest
Tutorial
Tutorial is loading...
Solution 1 (BledDest)
#include<bits/stdc++.h>
using namespace std;
const int N = 243;
struct edge
{
int y, c, f, cost;
edge() {};
edge(int y, int c, int f, int cost) : y(y), c(c), f(f), cost(cost) {};
};
int s, t, V;
vector<int> g[N];
vector<edge> e;
void add(int x, int y, int c, int cost)
{
g[x].push_back(e.size());
e.push_back(edge(y, c, 0, cost));
g[y].push_back(e.size());
e.push_back(edge(x, 0, 0, -cost));
}
int rem(int num)
{
return e[num].c - e[num].f;
}
int p[N];
int d[N];
int pe[N];
int inq[N];
bool enlarge()
{
for(int i = 0; i < V; i++)
{
d[i] = int(1e9);
p[i] = -1;
pe[i] = -1;
inq[i] = 0;
}
d[s] = 0;
queue<int> q;
q.push(s);
inq[s] = 1;
while(!q.empty())
{
int k = q.front();
q.pop();
inq[k] = 0;
for(auto z : g[k])
{
if(!rem(z)) continue;
if(d[e[z].y] > d[k] + e[z].cost)
{
p[e[z].y] = k;
pe[e[z].y] = z;
d[e[z].y] = d[k] + e[z].cost;
if(!inq[e[z].y])
{
q.push(e[z].y);
inq[e[z].y] = 1;
}
}
}
}
if(p[t] == -1)
return false;
int cur = t;
while(cur != s)
{
e[pe[cur]].f++;
e[pe[cur] ^ 1].f--;
cur = p[cur];
}
return true;
}
void process_test()
{
int n, k;
cin >> n >> k;
vector<int> a(n), b(n);
for(int i = 0; i < n; i++)
{
cin >> a[i] >> b[i];
}
s = 2 * n;
t = 2 * n + 1;
V = 2 * n + 2;
for(int i = 0; i < n; i++)
{
add(s, i, 1, 0);
add(i + n, t, 1, 0);
}
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
{
if(j < k - 1)
add(i, j + n, 1, -(a[i] + b[i] * j));
else if(j == n - 1)
add(i, j + n, 1, -(a[i] + b[i] * (k - 1)));
else
add(i, j + n, 1, -(b[i] * (k - 1)));
}
for(int i = 0; i < n; i++)
enlarge();
vector<int> order(n);
for(int i = 0; i < n; i++)
for(auto x : g[i])
{
int to = e[x].y;
if(to >= n && to < 2 * n && e[x].f == 1)
order[to - n] = i;
}
cout << k + (n - k) * 2 << endl;
for(int i = 0; i < n; i++)
{
cout << order[i] + 1 << " ";
if(i >= k - 1 && i < n - 1)
cout << -(order[i] + 1) << " ";
}
cout << endl;
e.clear();
for(int i = 0; i < V; i++)
g[i].clear();
}
int main()
{
int t;
cin >> t;
for(int i = 0; i < t; i++)
process_test();
}
Solution 2 (neal)
#include <algorithm>
#include <array>
#include <cassert>
#include <iostream>
#include <vector>
using namespace std;
template<typename T> ostream& operator<<(ostream &os, const vector<T> &v) { os << '{'; string sep; for (const auto &x : v) os << sep << x, sep = ", "; return os << '}'; }
template<typename A, typename B> ostream& operator<<(ostream &os, const pair<A, B> &p) { return os << '(' << p.first << ", " << p.second << ')'; }
void dbg_out() { cerr << endl; }
template<typename Head, typename... Tail> void dbg_out(Head H, Tail... T) { cerr << ' ' << H; dbg_out(T...); }
#ifdef NEAL_DEBUG
#define dbg(...) cerr << "(" << #__VA_ARGS__ << "):", dbg_out(__VA_ARGS__)
#else
#define dbg(...)
#endif
template<typename T>
void output_vector(const vector<T> &v, bool add_one = false, int start = -1, int end = -1) {
if (start < 0) start = 0;
if (end < 0) end = int(v.size());
for (int i = start; i < end; i++)
cout << v[i] + (add_one ? 1 : 0) << (i < end - 1 ? ' ' : '\n');
}
const int64_t INF64 = int64_t(2e18) + 5;
vector<int> assignment;
template<typename T>
int64_t hungarian(vector<vector<T>> costs) {
int n = int(costs.size());
int m = costs.empty() ? 0 : int(costs[0].size());
if (n > m) {
vector<vector<T>> new_costs(m, vector<T>(n));
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
new_costs[j][i] = costs[i][j];
swap(costs, new_costs);
swap(n, m);
}
vector<int64_t> u(n + 1), v(m + 1);
vector<int> p(m + 1), way(m + 1);
for (int i = 1; i <= n; i++) {
vector<int64_t> min_v(m + 1, INF64);
vector<bool> used(m + 1, false);
p[0] = i;
int j0 = 0;
do {
used[j0] = true;
int i0 = p[j0], j1 = 0;
int64_t delta = INF64;
for (int j = 1; j <= m; j++)
if (!used[j]) {
int64_t cur = costs[i0 - 1][j - 1] - u[i0] - v[j];
if (cur < min_v[j]) {
min_v[j] = cur;
way[j] = j0;
}
if (min_v[j] < delta) {
delta = min_v[j];
j1 = j;
}
}
for (int j = 0; j <= m; j++)
if (used[j]) {
u[p[j]] += delta;
v[j] -= delta;
} else {
min_v[j] -= delta;
}
j0 = j1;
} while (p[j0] != 0);
do {
int j1 = way[j0];
p[j0] = p[j1];
j0 = j1;
} while (j0 != 0);
}
// Note that p[j] is the row assignment of column j (both 1-based). If p[j] = 0, the column is unassigned.
assignment = p;
return -v[0];
}
void run_case() {
int N, K;
cin >> N >> K;
vector<int> A(N), B(N);
for (int i = 0; i < N; i++)
cin >> A[i] >> B[i];
vector<vector<int>> costs(N, vector<int>(N, 0));
for (int i = 0; i < N; i++)
for (int position = 0; position < N; position++)
if (position < K)
costs[i][position] = -(A[i] + position * B[i]);
else
costs[i][position] = -((K - 1) * B[i]);
int64_t score = -hungarian(costs);
dbg(score);
vector<int> solution;
for (int k = 1; k < K; k++)
solution.push_back(assignment[k]);
for (int k = K + 1; k <= N; k++) {
solution.push_back(assignment[k]);
solution.push_back(-assignment[k]);
}
solution.push_back(assignment[K]);
assert(int(solution.size()) == 2 * N - K);
cout << solution.size() << '\n';
output_vector(solution);
}
int main() {
ios::sync_with_stdio(false);
#ifndef NEAL_DEBUG
cin.tie(nullptr);
#endif
int tests;
cin >> tests;
while (tests-- > 0)
run_case();
}
Solution 3 (pikmike)
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define mp make_pair
#define pb push_back
#define sqr(a) ((a) * (a))
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define forn(i, n) for(int i = 0; i < int(n); i++)
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
typedef long long li;
typedef long double ld;
typedef pair<int, int> pt;
template <class A, class B> ostream& operator << (ostream& out, const pair<A, B> &a) {
return out << "(" << a.x << ", " << a.y << ")";
}
template <class A> ostream& operator << (ostream& out, const vector<A> &v) {
out << "[";
forn(i, sz(v)) {
if(i) out << ", ";
out << v[i];
}
return out << "]";
}
mt19937 rnd(time(NULL));
const int INF = int(1e9);
const li INF64 = li(1e18);
const int MOD = int(1e9) + 7;
const ld EPS = 1e-9;
const ld PI = acos(-1.0);
const int N = 100;
int n, k;
pair<pt, int> a[N];
bool read () {
if (scanf("%d%d", &n, &k) != 2)
return false;
forn(i, n){
scanf("%d%d", &a[i].x.x, &a[i].x.y);
a[i].y = i;
}
return true;
}
int dp[N][N];
int p[N][N];
void solve() {
sort(a, a + n, [](const pair<pt, int> &a, const pair<pt, int> &b){
if (a.x.y != b.x.y)
return a.x.y < b.x.y;
return a.x.x < b.x.x;
});
forn(i, N) forn(j, N)
dp[i][j] = -INF;
dp[0][0] = 0;
forn(i, n) forn(j, N) if (dp[i][j] >= 0){
if (dp[i + 1][j] < dp[i][j] + a[i].x.y * (k - 1)){
dp[i + 1][j] = dp[i][j] + a[i].x.y * (k - 1);
p[i + 1][j] = j;
}
if (dp[i + 1][j + 1] < dp[i][j] + a[i].x.y * j + a[i].x.x){
dp[i + 1][j + 1] = dp[i][j] + a[i].x.y * j + a[i].x.x;
p[i + 1][j + 1] = j;
}
}
vector<int> ans1, ans2;
int cur = k;
for (int i = n; i > 0; --i){
if (p[i][cur] == cur)
ans2.pb(a[i - 1].y + 1);
else
ans1.pb(a[i - 1].y + 1);
cur = p[i][cur];
}
reverse(all(ans1));
reverse(all(ans2));
printf("%d\n", sz(ans1) + sz(ans2) * 2);
forn(i, sz(ans1) - 1)
printf("%d ", ans1[i]);
for (auto it : ans2)
printf("%d %d ", it, -it);
printf("%d\n", ans1.back());
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
int tt = clock();
#endif
cerr.precision(15);
cout.precision(15);
cerr << fixed;
cout << fixed;
int tc;
scanf("%d", &tc);
while(tc--) {
read();
solve();
#ifdef _DEBUG
cerr << "TIME = " << clock() - tt << endl;
tt = clock();
#endif
}
}
Idea: adedalic
Tutorial
Tutorial is loading...
Solution (adedalic)
#include<bits/stdc++.h>
using namespace std;
#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())
#define x first
#define y second
typedef long long li;
typedef pair<int, int> pt;
const int MAG = 30;
int lst;
int n, k;
inline bool read() {
if(!(cin >> n >> k))
return false;
return true;
}
int ask(int l1, int r1, int l2, int r2) {
assert(l1 < r1 && l2 < r2);
assert(r1 <= l2 || r2 <= l1);
cout << "? " << r1 - l1 << " " << r2 - l2 << endl;
fore(i, l1, r1) {
if (i > l1) cout << " ";
cout << i + 1;
}
cout << endl;
fore(i, l2, r2) {
if (i > l2) cout << " ";
cout << i + 1;
}
cout << endl;
cout.flush();
string resp;
cin >> resp;
if (resp == "FIRST")
return -1;
if (resp == "SECOND")
return 1;
if (resp == "EQUAL")
return 0;
exit(0);
}
inline void solve() {
//check first position
mt19937 rnd(lst ^ (n * 1024 + k));
for(int q = 0; q < MAG; q++) {
int cur = 1 + rnd() % (n - 1);
int resp = ask(0, 1, cur, cur + 1);
if (resp == 1) {
cout << "! 1" << endl;
cout.flush();
return;
}
}
int len = 1;
while(true) {
int cnt = min(len, n - len);
int resp = ask(0, cnt, len, len + cnt);
if (resp != 0) {
assert(resp == -1);
break;
}
len <<= 1;
}
int lf = len, rg = min(2 * len, n);
while(rg - lf > 1) {
int mid = (lf + rg) >> 1;
int resp = ask(0, mid - lf, lf, mid);
assert(resp != 1);
if (resp == 0)
lf = mid;
else
rg = mid;
}
cout << "! " << lf + 1 << endl;
cout.flush();
lst = lf + 1;
}
int main() {
int tc;
cin >> tc;
lst = tc;
while(tc--) {
assert(read());
solve();
}
return 0;
}










Was skeptical about my approach of C2 but editorial gives a very simple easy to understand proof!
Problem D video editorial for N log^2 N approach: Link
Problem D video editorial for N log N approach: Link
I think you have mistakenly replied to me instead of commenting on main post, but anyway I will find it helpful as I couldn't solve D!
Well I guess your comment is at the top ( If he posts a new comment it will go to the bottom)
True that, many people prefer a video explanation, so just to reach out to everyone. I put it at here.
the problem D doesn't need any data structures.
it only needs binary search of answer.
Link : Link
The link is broken!
please help, I have implemented problem D-Multiset with binary search on fenwick tree.Expected time complexity(query*((log n)^2)) . but my code is showing TLE in test case 6. my code: please help .... thanks in advance.
You are getting TLE because of the slow input method. You can either use
cinwithios_baseorscanfI got AC with your code +
ios_base::sync_with_stdio(0); cin.tie(0)Submission link : 80917472
bro you are doing good dont care about the downvotes
Hey man , I got the point why it will be minimum at an angle of pi/4n but still not able to derive that cos/sin formula .. could u help?
I'll send you an image
Can someone please explain 1354C2 not so simple polygon embedding. I am not able to grasp editorial solution. Thank you.
Me too, and i really hope that someone could teach me using degree measure, not the radian measure.
Just replace every π with 180 in editorial.
Thus it will be using degree measure.
This could be helpful Here
Just consider the hexagon example in the editorial , You notice that the square has the same side length as the distance between the two opposite vertices(touching the square) in fig 1 , (2 units in the case of hexagon) Now draw a horizontal line between the 2 vertices (touching the square) in fig 1 , If you rotate this line anticlockwise , its horizontal component will start to decrease , but the horizontal component of the diagonal line between the vertices will start to increase , If you rotate a full (90/n) degrees it restores to its original fig1 (why 90/n , because at the center , the angle for each side is (360)/(2n) = 180/n , rotate half that is 90/n , and you achieve symmetry , or in other words the same figure ) Now , if after 90/n , the horizonal component of the diagonal turns to 2 , and for the horizontal vertices it decreases , then there must be a point where they both were same That point by symmetry has to be 90/2n i.e. in the middle
took a lot of time to prepare the tutorial. hope it's worth.
Although the tutorial for B is beautiful, I'd say Binary search was easier to think and implement!
Another simple approach is to iterate over the string and keep track of the most recent indices where each of the 3 digits appear. And at each step, if all 3 indices have valid values, take the difference between the maximum one of them and the minimum one plus one as candidate for the shortest length. Pick the minimum candidate as the answer.
hey! I implemented this approach. Getting the wrong answer. can you please tell me where it went wrong. Link:-https://codeforces.net/contest/1354/submission/80659788
Don't reset the values & decrement i when all three are present.
Got AC. Thanks :)
can u send the link of ur corrected code
here it is:- https://codeforces.net/contest/1354/submission/80663691
thanks
Comment deleted!!
Sorry guys but I don't understand why this comment is downvoted too much. Any explanation thanks?
I feel like the king who won the war at 7th attempts. I solved D with Java and submitted 6 times, either got MLE or TLE but submitted the same solution with C++ and got accepted.
There may be other possible solutions but if you want to use tree data structure, then I think you have to use either-
- BIT(Binary Indexed Tree)/fenwick tree which may get accepted in any languages.(I am bad at BIT)
- Or you can use segment tree with C/C++. (Segment tree might not gonna work with other languages. like my java solution.)
I believe your Java solution is fast enough, but
Scanneris extremely slow. You can still useBufferedReader, but you need to write your own I/O function like I explained here.Your (modified) submission
Thanks PizzaLovers007 for the idea and the modified submission. From now on I will use your idea for fast I/O function in Java.
1354D — Multiset My submission: 80598227 why i got wrong answer in test 52?Please help
is it possible to solve D with policy based data structures? i tried and got MLE on test 4.
update: so apparently the PBDS tree has two pointers per node plus the two values of the node, which gives us 4 ints per node in this case, and we have a maximum of 2 mil elements in the set (1m + 1m insertion queries), and so 2 mil * 16 bytes per node is well over the 28MB limit.
No BledDest replied on announcement page that pbds shall not pass.
but why, if n<=1e6, then total memory will be 4*1e6 bytes => 4MB which is less than 28MB, so why it gave MLE?
The ordered_set in pbds is implemented with balanced binary search tree. In order to have order statistics, more information need to be stored in each node.
Segment tree works on this problem with $$$O(4*N)$$$ memory and $$$O(nlogn)$$$ time complexity. You can check my submission for details here.
Anyone explain E please !
I will try to explain it in simpler terms for you. First, you need to understand that there cannot be any odd cycles in the graph. You can see this for yourself by drawing a cycle of length 3 and inducing for larger cycles.
With that out of the way, let's run BFS on each component, keeping track of the distance to each node from the starting node. If we ever encounter any odd cycles (i.e. the depth of an adjacent visited node is the same parity of the depth of the current node), we can terminate the program and print
NO. Otherwise, let's group all nodes with even distance from the starting node and claim that we can assign2to each of these. This is possible since they will each be separated by one and only one node, which we can assign1or3. With similar logic, we can assign2to all nodes with odd distance from the starting node. If the graph was guaranteed to be connected, we would already be done, by simply checking whether the number of odd distance nodes or the number of even distance nodes equalsn_2. However, there can be multiple components, leading us to the second part of the solution.Let's add the number of nodes with even distance as an item's weight in a knapsack problem, and do the same with the number of nodes with odd distance. These will also have a type number, which can just be its component id. This is crucial to understanding the rest of the solution. The
typeof an item represents which component it is in, and theweightof an item represents that we can assign exactlyweightwith nodes the number2in that component.To "merge" the components, we will run a very basic knapsack dp, with our state as
dp[i][j] = 1if it is possible to reach total weightjwith the firstitypes of items, anddp[i][j] = 0otherwise. The transition should be obvious, but notice that we cannot always dodp[i][j] = max(dp[i][j], dp[i - 1][j])since we must include exactly one item of each type (after all, we can't just forget to assign numbers to a component).Finally, we will check whether it is possible by checking whether
dp[total_components][n_2] = 1, since this represents that there is a way to assignn_2nodes the number2using all component types. If it is possible, we can simply backtrack for our solution, and we are done.Hopefully, this helps you understand the solution slightly better without any complicated terms.
while trying to solve the problem on my own I was able to deduce the impossiblity with odd length cycles.But then never did I realize that this would be using dp.So my question is what would be my intution to detect that this problem requires dp? Please Sir,if you can kindly help....
For me, it was realizing that the question would be impossible without being able to "merge" two components together, after solving the problem on one component. The second step is to really think about what the numbers you get from each component actually mean, and what
n_2really means. How does havingxnodes at an even distance help you? Only then will you realize that you are actually trying to find some set of numbers that sum to a specific number, which is a classical dp problem. You don't need much intuition to realize the correlation, just a lot of practice with solving questions of similar type, and knowing how to solve many classical problems.Why am I getting MLE in D if I use policy based data structures in C++?
Which data structure ?
pbds ordered set.....search fot it in geeks for geeks
Data structures like set, map or ordered set as you mentioned always require extra memory for pointer.
1354D — Multiset My submission: 80598227 why i got wrong answer in test 52?Please help
The memory limit was there I think to discourage the use of pbds. They most likely use extra memory to provide those extra functions. Sets and maps are anyway more memory hungry than simple vectors.
Is lazy needed for problem D?
I didn't use lazy in my solution, I updated the tree each time. It just take
log(n)to update the tree. Total time complexityn log(n)You may check my submission here
No, because it's single point update.
1354D — Multiset My submission: 80598227 why i got wrong answer in test 52?Please help
Try this case:
Should be 2, yours is returning 0.
Thanks!Solved
1354D — Multiset Getting W.A. on test case 12, Can someone provide a test case for why this fails?
thanks!
Sir,plz can you kindly explain how this binary search in problem D is working?What is it doing?Why it is taking the left bound as 0 and right bound as 10^6+1 all the time?I know the constraints on n and q but then the role of the binary search based on those 2 limits is not clear to me...Please Sir,I request you to guide me in this matter..Otherwise How will newbies learn?
$$$count\_le(x)$$$ is counting the number of elements in the multiset that are less than or equal to $$$x$$$. We're using this function to find the minimum element in the multiset. Suppose $$$L$$$ is the minimum element in the multiset. Then we know that for $$$x < L$$$, $$$count\_le(x) = 0$$$, and for $$$x \ge L$$$, $$$count\_le(x) > 0$$$. If we can find the smallest $$$x$$$ such that $$$count\_le(x) > 0$$$, then we know that $$$x$$$ has to be in the multiset.
The bounds on the binary search are set to be a value lower than any element in the multiset ($$$0$$$) and a value higher than any element in the multiset ($$$10^6+1$$$). I believe using $$$1$$$ and $$$n$$$ as bounds would work as well since all possible values of $$$x$$$ are in that range.
Please tell me why I am getting TLE in this submission for Multiset problem: https://codeforces.net/contest/1354/submission/80763648
Use fast I/O
Why it takes too much time for rating changes?
Problems B + C1 + D + E
Can somebody explain how the
count_le(int)in D works? I see the fairly simple code but still dont get it.The first for loop is straightforward, just count the number of elements less than or equal to x. In the second for loop, if the query is > 0 and if it is less than or equal to x then no matter when it is inserted it'll always contribute to count. As for the negative query, we now have count of elements less than or equal to x till this negative query, hence if the ordered statistics is more than count it won't affect our count as only numbers larger than x are removed. If the order statistics is less than our count, then we have to remove some smaller element hence we are decreasing count. Hope it helps.
Can someone explain how the function is monotonous in problem D editorial?
"The minimum in the resulting multiset is the minimum x such that this function returns non-zero for it, and since the function is monotonous, we can find the answer with binary search."
$$$f(x)$$$ — number of elements $$$<= x$$$ in the multiset.
When we go from $$$x$$$ to $$$x + 1$$$, all the elements $$$<= x$$$ will still be $$$<= x + 1$$$, but new elements (with value exactly $$$x$$$) may also contribute to $$$f(x + 1)$$$. So the value never decreases, thus $$$f(x)$$$ is monotonous.
Thanks, I got it why binary search is valid in this problem.
How is it guaranteed that the final value of rg will be present in the final array?
What's $$$rg$$$?
I'm supposing the minimum is $$$x$$$, so $$$f(x - 1) = 0$$$, while $$$f(x) > 0$$$, the same for all $$$x' > x$$$. So at the point $$$x$$$ $$$f(x)$$$ becomes positive, and we know that the element $$$x$$$ exists.
I was referring to the code in the editorial. Anyways, your reply solved my doubt, thanks!
The function actually returns the no of elements less than equal to x ,so for all elements less than the minimum element the function return a zero value as there are no elements less than the minimum element and for all elements greater than or equal to the min element the fun returns a non zero value(this value may increase by increasing the query element (or index))So it is monotonous because it returns 0 till a certain index and then returns non zero value till the last index.
Can anyone explain me How they are coming with solution for C1? I know people are saying it is easy to come up with this solution. But, still i'm not able to figure out this. Thanks.
The first thing i assume that the square will be somehow related to outer circle of polygon. And equation of outer circle of a regular polygon is very easy to figure out. You can search on google for this equation.
And finally came to an equation for C1 that a be sides of square, r be radius of outer circle then, a*a/4+0.5*0.5=r*r. You can simply get it drawing figure.
For C2 i get it that a polygon having 2*n sides will fit in a square having sides equal to half of radius of polygon having 4*n sides. Although i don't have a solid proof for this but it passed.
I can tell you my weird approach during the contest but editorial is much simpler. I divided the square into 4 quadrants just like a cartesian coordinate system and then we can tell each quadrant contains $$$(n / 2)$$$ vertices since $$$n$$$ is even. Now see the pic we are starting from the coordinate $$$(0, 0)$$$ then finding the next coordinate $$$(x_i, y_i)$$$.
The main idea is to find the distance between the initial position and the final position. During the contest, I was not sure if that is true or not.
for finding the final position we can iterate $$$n$$$ times and use this simple formula $$$(x_{i + 1}, y_{i + 1}) = (x_i + cos(theta), y_i + sin(theta))$$$, and increase $$$theta$$$ by $$$δ$$$ in every iteration.
Did you notice the formula is not giving the expected value?. here is the reason-
logically our initially starting position should be $$$(x_1, y1)$$$ instead of $$$(0, 0)$$$, but what I did is shift the $$$(x_1, y_1)$$$ by $$$(-0.5)$$$, and ultimately you will land upon the final position according to the figure.
my submission
Can anyone please explain how the final expression in C2 is obtained?
Just consider a horizontal line through the center of the polygon in fig. 1 of Tutorial. This is the side of the square initially. Now rotating the polygon by angle x, this line also rotates by same angle and the new square side becomes cos(x) times initial. In this problem x=pi/(4*n) and you just need to figure out the initial square side which is nothing but distance between two opposite vertices of the polygon.
Thanks for the explanation. I understood
Can you explain why angle x = 90 / 2 * n?
See the Tutorial, its explained beautifully!
I just see "if we rotate, not a reason why are you doing it. Is it that intuitive?
Suppose you are given a square and hexagon of fixed size. You want to fit the hexagon in the square. How will you do it? First you will try to fit it in a straight forward way by placing the hexagon above the square. If it dosen't fit , you will rotate and try to fit.
Also this doesn't answer to my question. How do you come up with that angle?
Symmetry! You can also prove it mathematically. Start from 0 degrees. Now start rotating, at first the length decreases and width increases. After pi/(4*n) the reverse thing happens. This cycle is repeated once the angle becomes pi/(2*n). So, between 0 to pi/(2*n) the side length of square(which is max(length,width) ) first decreases then increases. So minima at pi/(4*n).
I understand that, but why divided by 2 * n?
I strongly feel that you haven't spent much time with the tutorial. This much of explanation is enough for anyone to understand. Nevertheless , try searching concepts like ternary search, maxima/minima. Try watching videos on rotating polygon and visualizing.
A detailed mathematical proof is also given below.
Let us rotate point $$$B$$$ clockwise, and point $$$D$$$ against. This is the same as rotating the point $$$D^{'}$$$. On the one hand, the projection onto the line increases, and on the other, decreases. To select the side of the square, we need to choose the maximum of these projections. Then the minimum side of the square will be under conditions when both projections are equal, that is, on the bisector $$$OM$$$. Now consider the $$$BOD^{'}$$$ triangle, it is isosceles and we know what $$$OB$$$ is equal to. Then, from the condition that $$$OB$$$ is equal to $$$OM$$$, we find the desired projection.
This is the half part of the square side.
Thanks for the proof
How do we arrive at the formulas for C1 and C2?
For C1, I solved it with a different approach. Basically the formula for internal angle of a n-sided polygon is given by
theta = ((n-2)*180))/nWe form a triangle as shown in the editorial. The side bisects the internal angle, lets saytheta1 = theta/2Sotan(theta1) = x/0.5Thereforex = tan(theta1)/2Inorder to find the length of square we multiply x with two. Thus final ans isans = tan(theta1)Link to my submissionI understood it same way just now.
did you implement this in CPP?
Yes, I implemented in Cpp. Here: 80607062
I don't get these two lines. can you please explain? double ang = 90-((1.0*90)/n); ang = ang*acosl(-1.0l)/180;
Maximum radius Circle which can be inscribed in regular polygon is also the maximum radius circle which can be inscribed in square(which embeds the regular polygon). So, size of square is equal to radius of circle*2
From pic, you can see clearly that ang = (90-90/n). and in second line(ang = ang*acosl(-1.0l)/180;) I converted angle into radians from degrees.
Try this. You are actually trying to get the length of the purple line, which can be divide into (n-1) parts. In this case, 3 parts. I've separated the purple line with blue lines. The first part(from down to up) should be 1 * sin(theta). The second part should be 1 * sin(theta * 2). The third part should be as same as the first part, which is 1 * sin(theta). btw, theta = 180° / n P.S. this is written in degree, not radian.
You are actually trying to get the length of the purple line, which can be divide into (n-1) parts. In this case, 3 parts. I've separated the purple line with blue lines. The first part(from down to up) should be 1 * sin(theta). The second part should be 1 * sin(theta * 2). The third part should be as same as the first part, which is 1 * sin(theta). btw, theta = 180° / n P.S. this is written in degree, not radian.
For C1, note that for a regular polygon with even number of sides, opposite sides will be parallel. For even n, 2*n will also be divisible by 4. And by symmetry argument, there will be two pairs of opposite parallel sides perpendicular to each other. So we can align the polygon so that this 4 sides will be parallel to the sides of the square, and also touching them to minimize the size of the square.
Now consider the center of symmetry of the regular polygon, which is also the center of the inscribed circle, of the circumscribed circle, as well as of the square. Construct the triangle with one of the sides of the polygon as base and the center of the polygon as third vertex. The height of this isosceles triangle will be half of the side of the square. The angle of the triangle with tip in the center of the polygon measures 360 deg / (2*n) or 2* pi / (2*n). Construct the height of the triangle. It will split the isosceles triangle into 2 rectangular triangles, whose angle with the tip in the center of the polygon will measure half of the previous angle or pi / (2*n). Tangent of the angle equals to the ratio of the opposite cathetus (half of the side of the regular polygon) to the adjacent cathetus (the height we are looking for). So h = 0.5 / tan(pi / (2*n)), and the side of the square is twice that.
For C2, if we try to align the polygon to have a pair of sides parallel with a pair of sides of the square, then the other 2 sides of the square will touch 2 opposite vertices of the regular polygon, and the distance between 2 opposite parallel sides of the polygon will be shorter than the side of the square, leaving a gap. The long diagonal connecting the 2 vertices touching the sides of the square will also be parallel to 2 opposite sides of the polygon. If we rotate the polygon by the angle pi / (2*n), the situation will be the same, except now vertices of the polygon are touching the other pair of sides of the square. By symmetry, the optimal rotation angle should be midway between these 2 positions, i.e. it is equal to pi / (4*n). The long diagonal will now touch 2 opposite sides of the square like before, but it is at a slant angle (equal to pi / (4*n)) respective to the other pair of sides, instead of parallel.
To calculate the diagonal length, construct the similar isosceles, and then rectangular triangles as we used in problem C1. The hypotenuse of the rectangular triangle is half of the diagonal, and it equals 0.5 / sin(pi / (2*n)), since sine of the angle is the ratio of the opposite cathetus and the hypotenuse. The full diagonal is 1 / tin(pi / (2*n)).
To calculate the length of the side of the square, project the diagonal on to the direction parallel to the side of the square (this can also be thought of as constructing a rectangular triangle with the side of the square as one of the catheti and the diagonal of the polygon as the hypotenuse), to obtain the side of the square being equal to cos(pi / (4*n)) * 1 / sin(pi / (2*n)).
May be this will be helpful for you to understand the derivation of formulas to both C1 and C2 problems.
Problem C1 and C2 Vedio Explanation | Educational Codeforces Round 87
Any program where I can draw and rotate the drawings in problem C2 ?
I think Geogebra should do the trick.
Have a try at wolfram alpha. It is an online application,but I think it is a good choice for you.
Can anyone explain this code to me. 80463378 This is a solution of C1 and C2.
Like both the ideas of C1 and C2. One problem, two datas, two levels of difficulty.
At first I wasn't a huge fan of problem D because I thought Fenwick/segment tree was the only solution. Having seen this editorial though, I realize it's actually very creative and interesting.
Overall, I feel I learned a lot from this Educational Round. Thank you to all the problem writers!
PLEASE explain the BINARY SEARCH and the TWO POINTERS solution for the problem 1354B. I will be grateful.Thank you.
We will use binary search on the length of the substring. Notice if the substring of size t contains all the characters, then the substring of size t+1 also contains all the characters.
Let say we have a function check(t) which returns True if there exists a substring of size t such that it contains all the characters. Then we can use something like this.
Now to implement check(t) we can use sliding window technique. Try implementing it yourself.
You're looking for this : Comment Here's the 2/3 Pointers(?)
For Binary search, you do it on the length and find the minimum length of the subarray with at least one of each character. You need to have the count of each character beforehand and you can use prefix sums for that: Binary Search
That does not look like "two pointer" to me.
Yeah, that's 3-Pointer actually, but it serves the purpose, I think.
Regardless of how many "pointers" you can count, that has nothing to do with two pointer technique. It is rather a sort of dp where at each step you have the shortest substring ending at the given position.
If there are 3-pointers keeping track of each of the character's latest position, I think I'll use that term. I may be wrong!
Please explain D solution via Fenwicks tree.
We will use the frequency array to build the Fenwick tree. Let's say we have an array freq[1..n] that contains the frequency of all the numbers given in the array, i.e if freq[y] = x, then the number y appears x times in the given array.
For the query of the first type "add integer K to the multiset" we simply need to increase the freq[k] by 1.
For the query of second type, we need the smallest number x such that freq[1] + freq[2] + freq[3] + ... + freq[x] is greater than or equal to k. Then we can just decrease the freq[x] by 1.
Let's say we have functions update(t, val) and getSum(t).
update(t, val) increases the value of index t by val. freq[t] += val.
getSum(t) returns freq[1] + freq[2] + freq[3] + ... + freq[t] in log(n) time.
Then for the query of type one simply use update(t,1). For the query of the second type use Binary search to find the required number and use update(t,-1).
To find the required number use something like this
Finally for the output, just do a linear search to find smallest t such that getSum(t) > 0 and output t.
Here is my submission. 80502866
Can't understand why getSum(t) use log(n) time.
Update and query takes log(n) time in Fenwick Tree.
Not working in java
Can anyone please tell what is wrong in this approach...
this is showing wrong ans on 2 test case set at 163rd entry...
please kindly help..
AVOID COPY PASTING ENTIRE CODE IN COMMENT SECTION
you can maybe try i/p 1 122321223
o/p for this will be 3. If you need a reason, do let me know :D
How to solve c2 by ternary search ?
In problem c1 , how to prove that solution in the editorial is the best one ? Since we can rotate the polygon , there might exist some other orientation such that answer is better than the one editorial ?
essentially, they're using the height of the octagon (or n-gon) from one midpoint of a side to another as the height of the square. any other rotation would increase the size due to pythagorean theorem. take for example, if you used opposite vertices, that would be greater than the two midpoint solution because of pythag theorem (the legs are always smaller than hypotnuse)
edit: wait nvm it's either the midpoint or the vertice, but either way its guaranteed to be one of those because those are the maximums and minimums respectively
Look at an inscribed circle of $$$2n$$$-gon. Since $$$2n$$$-gon should be embedded in the square and the circle is embedded in $$$2n$$$-gon then the circle must be embedded in the square. And there is no way to embed the circle in the square with side lower than the diameter of the circle.
But we've shown the example with the square side equal to the diameter, so it's the best answer.
I had another approach to C1 (which then can easily be related to C2, as I just checked after seeing the editorial) and I'm not sure if it was explained in the comments.
I noticed that when you have a $$$2n$$$-gon with $$$n$$$ even, you can see that (knowing that the best disposition of the polygon inside the square is when two paralel sides of it are also paralel with a pair of ones in the square) the width of the square, and hence, its side length, is the sum of the lengths of one of the legs of each of the right triangles defined by the number of "not-right" sides in a quadrant, times two, as it replicates symmetrically on the opposite quadrant, and also add it $$$1$$$, as it's the length of one of the sides that is paralel to the ones I mentioned in the square:
Note how the internal angle of each of the triangles formed between the vertices and the center of the polygon are the same as in the triangles I mentioned before. Here's another example in a dodecagon ($$$n = 6$$$):
Knowing all of this, and the fact that I can get the angle of those triangles that "make" the polygon as the amount of sides in half of the polygon (which is $$$n$$$) and the total angle that makes it ($$$\pi rad$$$ or $$$180°$$$), given that it's a regular polygon, it would be $$$\frac{\pi}{n}$$$. And then each of the angles you see it's a multiple of one of them (in the dodecagon, $$$30°, 60°...$$$) as they are all equal and adjacent. Finally, the length of the leg of each right triangle I mentioned before, would be $$$cos(\frac{\pi}{n}*j)$$$ (taking for example, the horizontal one), being the $$$j$$$-th counting, for example, from the bottom. And as it also adds symetrically, it is $$$2*cos(\frac{\pi}{n}*j)$$$.
I can repeat doing that for all $$$j$$$ in $$$[1,\frac{N}{2}]$$$ with a loop, then add it one, and there's your answer.
As some pointed out, one way to see C2, is by calculating the distance between opposite sides of the polygon (taking it with a segment perpendicular to both), and then it seems the optimal solution is to rotate the polygon by $$$\frac{\pi}{4n}$$$. As my approach exactly gets that value, for C2 the only thing to do multiply the answer by $$$cos(\frac{\pi}{4n})$$$, which is getting the rotated segment, and by so the optimal width of the square.
My solution may be worse than the editorial as it has a complexity of $$$O(n)$$$, but I think it's still a nice approach to the problem.
Submissions: C1 C2
I hope I explained it well and may be useful to someone :)
DUDE, I had the same solution but i kept on getting double error or something, like my solution was 0.3 off for test case N=200 for c1. I think I either messed up my implementation or java is poop
Sorry for off-topic but can you please tell the graphing tool that you are using ?
I used GeoGebra's Geometry Tool.
Can anyone tell me what is wrong in my submission of 1354B- Ternary String question! Please have a look at the following submission:
https://codeforces.net/contest/1354/submission/80626322
1354D — Multiset My submission: 80598227 why i got wrong answer in test 52?Please help
Can anyone explain the editorial for B more elaborately?
have a look on https://codeforces.net/contest/1354/submission/80605650
I created a vector A which tells the order of 1,2,3's , and vector B storing their particular frequencies...
As in if you have a string 332111111221132, then
A : 3 2 1 2 1 3 2
B : 2 1 6 2 2 1 1 (hope u get what I've done till now)
Now just simply iterate A from 2nd to 2nd last position and check that if A[i-1],A[i],A[i+1] all are different (if they are different we can get substring of form 122...223(or something similar), in that substring A[i] will occur B[i] times and A[i-1] and A[i+1] will occur once). Finally we will be finding min of (B[i]+2) whenever A[i-1],A[i],A[i+1] are different...
Hope this helps, do let me know if you need more help :D
I tried to develop a solution for problem 1354C1 - Просто вписываем многоугольник by using each triangle rectangle with hypotenuse = 1. My solution just makes the sum over the cosine of each angles below the right angle of the triangles i talked before. The cosine of each angle in blue on the image is the length of the red segment, and i make the sum until i get to the right segment in blue, then i multiply what i already got by 2 because this is the part above the straight segment in blue, and sum 1 which is the length of the straight segment in blue.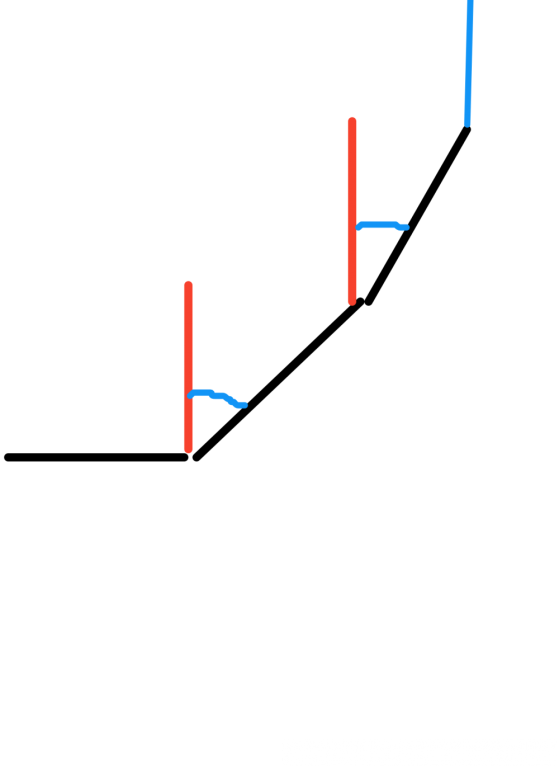
The code:
I start with the first angle and then i decrease the angle by a rate. The angle i start with is just the angle of the regular polygon minus 90. And the angle should decrease after each vertex until it gets to 0 ( when we reach the straight segment). The rate is the first angle divided by n/2-1 which is the number of vertices until the straight segment and after the first vertice.
For the test case: 1 200
My solution gives the answer: 127.46243899 Which is not the correct one, but i can't find out if the solution is not correct or i'm just having a lot of floating point errors on the sum. Thank you.
I did the same but I am said about it
I'm sorry, did you mean sad?
The cos function takes the angle in radians as the argument, not the angle in degrees. Also, beg shouldn't be an int.
Thank you very much. I was thinking that the starting angle would always be an integer, and my fear of losing precision made me use int.
I still had to simplify some equations, the final solution is 80647479
Problem C1/2 can also be solved by brute force. In detail, you can rotate the polygon within [0, pi/n) for 1000 times. [submission:80507571]
so you test every possible combination of opposite vertice and midpoint height and take the maximum?
no need for midpoint
I also solved it by brute force in O(n/2) time complexity: 80679036
It is quite obvious from the image that if we know the angle we can find the orange line, so looping through n/2 angles we need to find the longest orange line, which leads us to the answer = 2 times longest orange line.
It is definitely not the best solution, but at least it is simple enough to understand for the beginners like me ))
The editorial of D , which was explained without data structures was simply awesome.
Please can you explain me how to solve D.Multiset without segment tree or anything like it.I am unable to understand the tutorial.Thanks in advance
Ok, so if we look carefully at the problem statement what matters after all is that we need to return any element that still belongs to the multiset. Now generally in these types of questions the easiset is to track something like minimum or the maximum element, so here it is easy to keep track of the min element. Now as the queries are offline, so we can simply keep track of the smallest element using binary search.
Actually D could be solved in linear: 80679881 (It cost me a few times to shrink the memory >_<)
Can you give a brief explanation? Thank you
Firstly we can do some preprocessing to make each number inserted exactly once. Then while doing the binary search, the insertion and deletion in the rest half part could be discarded. Then the complexity would be $$$T(n) = T(n/2) + \Theta(n)$$$.
Wouldn't that be O(nlogn) ?
N + N / 2 + N / 4 + N / 8 + N / 16 + ... is 2*N so it's O(N)
in div2 D, what is guarantee that if count_le(mid) > 0 ,then element is present in multiset and even if it is present , then how do we know it will not be removed as a result of k operations. e.g : 5 4 1 2 3 4 5 -5 -1 -3 -1 Here, for element 4, count = 1, but it gets removed from the multiset. How is the solution working?
Edit: all good.
I think you're looking at the judge output, your output had
Oh crap, sorry, you're right.
1354D — Multiset Getting W.A. on test case 12, Can someone provide a test case for why this fails?
Could someone let me know how this solution for E is wrong? It's not the conventional method used in the solution, but I thought it would still work: https://codeforces.net/contest/1354/submission/80695289
how to solve D without using any data structure. Someone please explain
It's already in the editorial
i am not able to understand the tutorial for problem D.Can you please explain ??
But this is giving incorrect answer for figures other than hexagon . Is there any error in my assumption ?
my submission : link
Thanks
$$$\angle{CAB} = 45^{\circ}$$$ only for a hexagon, so it works only for a hexagon.
I have a solution for C2 which uses binary search: we can see that a pair of points with the longest distance between them in the 2n-gon, here hexagon, are B and D.
So, we may try to keep these points along the diagonal of the square (as diagonal is the longest distance between two points on a square)
But we still have to leave out some distance ED = BH = x from both ends of the diagonal, and then only place the hexagon's vertices. Because if we try to co-incide the opposite vertices, with the end points of the squares diagonal then since the interior angle of the figure > 90, hence it won't work, it will leave the square.
So, we look for some minimum length x = ED = BH which on leaving out from both ends we may fit the figure inside the square.
On this length x, we may perform a binary search!
80725776
Can you please explain how to perform the binary search in this case ?
I understood the rest of the part.We are finding length of the diagonal such that the square it forms just covers whole polygon.Thus during binary search , we will see if it covers the polygon .How to do that ?
let the longest distance in the hexagon be 'dist'. Then diagonal of square is 2x + dist let the square have its bottom left corner at 0,0 then we can find point E at (x/sqrt(2), x/sqrt(2)).
Then using knowledge about the angles of the hexagon, we shoot a vector of length 1 at the appropriate angle from E, then from that point we shoot another vector of length 1 and so on....
to get the points of the hexagon, then we simply check whether these points lie within the square, by checking their x and y co-ordinates all must be between 0 and 'side.
E might not necessarily lie on the corner of the square so how it's coordinate is (x/sqrt(2),x/sqrt(2)).can you please elaborate the process ?
the bottom left corner of the square is (0,0) then E is at x distance from it along the diagonal, hence it is at (x/sqrt(2), x / sqrt(2))
In case anyone need Detail explanation for C1 and C2 Here
Why is segment tree expected to pass in D when ordered_set fails. Only reason to not use ordered_set in C++ is because it will have 2*n nodes at worst. But segtree also needs 4*n nodes. Please clarify.
can anyone explain why my solution gives TLE on test case 4 . even though it is O(N*log(N)*log(N)) code — 80806088
I don't understand why my solution gets TLE on testcase 4 . here is the link. can anyone help please?
I think the same happened with me too. like how does O(N*logN * longN) solution gives TLE.
Code for Multiset 1345-D I am getting Time Limit exceeded for test case 6 can someone pls help?
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
try to put these lines at the begin of your main, this will make your code faster.
Here's my problem solving stream. I didn't bother explaining what I was doing (like when teaching), only thinking out loud.
Can someone please help me with problem F, don't know why this solution is TLEing on test 32: https://codeforces.net/contest/1354/submission/81679962
According to the author 's solution to problem F, I wonder why the constraints are too small and time limit is too high?
Can someone please discuss the binary search approach of the ternary string question?
Can someone please tell me what is wrong in my java solution for D. I am getting a MLE on Case 8.
import java.io.BufferedReader; import java.io.IOException; import java.io.InputStreamReader; import java.io.PrintWriter; import java.util.StringTokenizer;
public class Solution{
}
Solved D using the Fenwick tree + Binary search without any optimization. Here is the submission. Idea is to keep frequency bit array.
Question G — Find a Gift
This can be solved deterministically with 4*logn i.e. 40 queries in the worst case. You can find a stone deterministically in 20 queries. Method -> let a = {1,2,...n/2,...n} -> Divvy it up in two sets and compare their weight. Then change a to the set with greater weight. If a is odd, remove one element and append to another vector say 'B'. Finally doing it recursively, we would stop with a single element. Add this element to B. The above task in done with 10 queries. Now, simply find the max element in B by asking at most of logn queries. Then the rest is similar to the editorial. Submission 100589414 for reference [Although the code is extremely messy]
If I understood correctly it may not work for this case, am I missing something?
But 9 is not a stone.
For D I have written a n(logn^2) solution using segment tree and fenwick tree separately
but my segment tree solution gave TLE and fenwick tree passed but both of these data structures have same complexity, which is nlogn, right?? or if not how fast is fenwick tree?
Segment tree solution which gave TLE — https://codeforces.net/contest/1354/submission/233261831 Fenwick tree solution which passed — https://codeforces.net/contest/1354/submission/233262440
As segment tree consumes more memory and isn't faster than fenwick tree, its bound to happen due to stricter time & memory limits.