This is our first contest for the three of us (Alexdat2000, crazyilian, sevlll777), so we would like to share our impressions of creating this contest. Check it if you want to!
First problem — task rejections. 300iq rejected about 13 problems, 6 of which were supposed to be problem D. In the end, we came up with E, and the old E moved to D.
These are the verdicts with which the problems were rejected:
- The idea is very simple here and the implementation is very simple too, this problem is definitely not D1C-D and definitely not interesting.
- Not an interesting problem, too standard, without new ideas.
- This is a known problem which is solved quite simply by a compressed tree.
- Unfortunately, it seems to me that this problem does not fit D1B. It is a funny construct but it is too technical (not interesting enough) for this position and too simple for the next ones.
- This problem is solved very simply by taking a close look at the sequence, so it is not very interesting.
- It seems to me that this problem is too standard. It is as if in the condition it is written, which dp should be written.
- The idea of 4 consecutive numbers is known.
- It's a known problem.
- It's a known problem.
- It's too standard.
- There's some greed in there. Is that the right thing to do?
- Well, first of all, it's doubtful you have any proof. Second of all, isn't that on oeis?
- It doesn't make her any better, it's a known problem.
When the problems were already formed, their creation began. In some problems, it was necessary to lower the constraints, which made it impossible to cut off some non-deterministic or not optimal solutions.
Otherwise, everything was fine until the last 18 hours before the contest began...
- Mike MikeMirzayanov Mirzayanov sent 7 issues to problem A. It was necessary to redo all the tests in the problem and much more.
- While we were correcting them, coordinator Ildar 300iq Gainullin told us to remove all the illustrations for the problem (memes and just cool pictures at the bottom of the notes). We did not like it very much, we wanted the pictures to be included in the contest.
- We finished fixing problem A, and went to bed. At that time Ildar (thank him very much) was polishing the conditions of all the other problems. Unfortunately, at that moment he removed the pictures. He also suddenly renamed problem F and city in the English version of problem D.
- 4 hours before the beginning. Mikhail Mirzayanov started sending issues to other problems.
- We had to redo almost all the tests for problems B, C and D.
- Heroically won the limits in E 2 hours before the contest start.
A total of 475 commits to the Polygon were made.
During the round there were many of the same type, but also some funny clares. For example:
- Problem C. i cant solve it
- Problem E. When will a COVID 19 vaccine come out???
Thanks to everyone who upvotes this editorial!
And, of course, here's the tutorial of the round.
1358A - Park Lighting
Idea: Alexdat2000

#include <iostream>
using namespace std;
int main() {
int t, n, m;
cin >> t;
while (t--) {
cin >> n >> m;
cout << (n * m + 1) / 2 << '\n';
}
}
1358B - Maria Breaks the Self-isolation
Idea: crazyilian

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void solve() {
int n;
cin >> n;
vector<int> arr(n);
for (int &el : arr)
cin >> el;
sort(arr.begin(), arr.end());
for (int i = n - 1; i >= 0; i--) {
if (arr[i] <= i + 1) {
cout << i + 2 << '\n';
return;
}
}
cout << 1 << '\n';
}
int main() {
int t;
cin >> t;
while (t--)
solve();
}
1358C - Celex Update
Idea: crazyilian

#include <iostream>
using namespace std;
int main() {
int t;
cin >> t;
while (t--) {
long long a, b, c, d;
cin >> a >> b >> c >> d;
cout << (c - a) * (d - b) + 1 << '\n';
}
}
1358D - The Best Vacation
Idea: sevlll777

#include <iostream>
#include <algorithm>
#include <vector>
#define int long long
using namespace std;
signed main() {
int n, len;
cin >> n >> len;
vector<int> A(2 * n);
for (int i = 0; i < n; i++) {
cin >> A[i];
A[n + i] = A[i];
}
n *= 2;
vector<int> B = {0}, C = {0};
for (int i = 0; i < n; i++)
B.push_back(B.back() + A[i]);
for (int i = 0; i < n; i++)
C.push_back(C.back() + (A[i] * (A[i] + 1)) / 2);
int ans = 0;
for (int i = 0; i < n; i++) {
if (B[i + 1] >= len) {
int z = upper_bound(B.begin(), B.end(), B[i + 1] - len) - B.begin();
int cnt = C[i + 1] - C[z];
int days = B[i + 1] - B[z];
int too = len - days;
cnt += ((A[z - 1] * (A[z - 1] + 1)) / 2);
cnt -= (((A[z - 1] - too) * (A[z - 1] - too + 1)) / 2);
ans = max(ans, cnt);
}
}
cout << ans;
}
1358E - Are You Fired?
Idea: sevlll777 и crazyilian

#include <iostream>
#include <vector>
using namespace std;
#define int long long
signed main() {
int n;
cin >> n;
int N = (n + 1) / 2;
vector<int> a(N);
for (int &el : a)
cin >> el;
int Ax;
cin >> Ax;
vector<int> m(N + 1, 0);
int Pprefsm = 0;
for (int i = 1; i < N + 1; ++i) {
Pprefsm += Ax - a[i - 1];
m[i] = min(m[i - 1], Pprefsm);
}
int Aprefsm = 0;
for (int k = 1; k <= N; ++k)
Aprefsm += a[k - 1];
for (int k = N; k <= n; ++k) {
if (Aprefsm + m[n - k] > 0)
return cout << k, 0;
Aprefsm += Ax;
}
cout << -1;
}
1358F - Tasty Cookie
Idea: sevlll777 и crazyilian

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int LIM = 2e5;
bool is_increasing(const vector<int> &vec) {
for (int i = 0; i < vec.size() - 1; i++) {
if (vec[i] >= vec[i + 1])
return false;
}
return true;
}
bool is_decreasing(const vector<int> &vec) {
for (int i = 0; i < vec.size() - 1; i++) {
if (vec[i] <= vec[i + 1])
return false;
}
return true;
}
vector<int> rollback(const vector<int> &vec) {
vector<int> ans(vec.size());
ans[0] = vec[0];
for (int i = 1; i < vec.size(); i++)
ans[i] = vec[i] - vec[i - 1];
return ans;
}
signed main() {
int n;
cin >> n;
vector<int> a(n), b(n);
for (int &i : a)
cin >> i;
for (int &i : b)
cin >> i;
vector<int> a_rev = a;
reverse(a_rev.begin(), a_rev.end());
if (n == 1) {
if (a == b)
cout << "SMALL" << '\n' << 0 << '\n';
else
cout << "IMPOSSIBLE" << '\n';
return 0;
}
int sum_a = accumulate(a.begin(), a.end(), 0LL);
int sum_b = accumulate(b.begin(), b.end(), 0LL);
int rollback_cnt = 0;
if (n == 2) {
vector<int> ans; // -1 = R, X = PPP..PP (x times)
int move_cnt = 0, roll_cnt = 0; // both types
bool rev = a[0] > a[1];
if (rev)
swap(a[0], a[1]);
if (b[0] > b[1]) {
swap(b[0], b[1]);
ans.push_back(-1);
move_cnt++;
}
while (true) {
if (sum_a > sum_b) {
cout << "IMPOSSIBLE" << '\n';
return 0;
}
if (sum_a == sum_b) {
if (a != b) {
cout << "IMPOSSIBLE" << '\n';
return 0;
}
if (rev) {
ans.push_back(-1);
move_cnt++;
}
if (rollback_cnt > LIM) {
cout << "BIG" << '\n' << rollback_cnt << '\n';
return 0;
} else {
cout << "SMALL" << '\n' << move_cnt << '\n';
reverse(ans.begin(), ans.end());
for (auto i : ans) {
if (i == -1)
cout << "R";
else {
for (int _ = 0; _ < i; _++)
cout << "P";
}
}
cout << '\n';
return 0;
}
}
if (a[0] == b[0]) {
if ((b[1] - a[1]) % b[0] == 0) {
roll_cnt = (b[1] - a[1]) / b[0];
ans.push_back(roll_cnt);
move_cnt += roll_cnt, rollback_cnt += roll_cnt;
b = a;
sum_b = b[0] + b[1];
} else {
cout << "IMPOSSIBLE" << '\n';
return 0;
}
} else {
roll_cnt = b[1] / b[0];
ans.push_back(roll_cnt);
move_cnt += roll_cnt, rollback_cnt += roll_cnt;
ans.push_back(-1);
move_cnt++;
swap(b[0], b[1]);
b[0] %= b[1];
sum_b = b[0] + b[1];
}
}
}
string ans;
while (true) {
if (sum_a == sum_b) {
if (a_rev == b) {
ans.push_back('R');
reverse(b.begin(), b.end());
}
if (a == b) {
reverse(ans.begin(), ans.end());
if (rollback_cnt > LIM)
cout << "BIG" << '\n' << rollback_cnt << '\n';
else
cout << "SMALL" << '\n' << ans.size() << '\n' << ans << '\n';
} else
cout << "IMPOSSIBLE" << '\n';
return 0;
} else if (is_increasing(b)) {
b = rollback(b);
sum_b = accumulate(b.begin(), b.end(), 0LL);
ans += 'P';
rollback_cnt++;
} else if (is_decreasing(b)) {
reverse(b.begin(), b.end());
ans += 'R';
} else {
cout << "IMPOSSIBLE" << '\n';
return 0;
}
}
}
#include <bits/stdc++.h>
using namespace std;
#define int long long
signed main() {
int n;
cin >> n;
vector<int> a(n), b(n);
for (int i = 0; i < n; ++i) cin >> a[i];
for (int i = 0; i < n; ++i) cin >> b[i];
if (n == 1) {
if (a[0] == b[0]) cout << "SMALL\n" << 0;
else cout << "IMPOSSIBLE";
return 0;
}
if (n == 2) {
vector<pair<int, bool>> res;
int kol = 0;
while (true) {
if (b[0] == 0 || b[1] == 0) {
cout << "IMPOSSIBLE";
return 0;
}
if (a == b) break;
if (a[0] == b[1] && a[1] == b[0]) {
res.emplace_back(1, false);
break;
}
if (b[0] == b[1]) {
cout << "IMPOSSIBLE";
return 0;
}
if (b[0] > b[1]) {
res.emplace_back(1, false);
swap(b[0], b[1]);
}
if (a[0] == b[0] && a[1] < b[1] && a[1] % b[0] == b[1] % b[0]) {
res.emplace_back((b[1] - a[1]) / b[0], true);
kol += res.back().first;
break;
}
if (a[1] == b[0] && a[0] < b[1] && a[0] % b[0] == b[1] % b[0]) {
res.emplace_back((b[1] - a[0]) / b[0], true);
kol += res.back().first;
res.emplace_back(1, false);
break;
}
kol += b[1] / b[0];
res.emplace_back(b[1] / b[0], true);
b[1] %= b[0];
}
if (kol > 2e5) {
cout << "BIG\n";
cout << kol;
} else {
cout << "SMALL\n";
int flex = 0;
for (auto i : res) flex += i.first;
cout << flex << "\n";
for (int i = res.size() - 1; i >= 0; --i) {
for (int j = 0; j < res[i].first; ++j) {
if (res[i].second) cout << "P";
else cout << "R";
}
}
}
return 0;
}
vector<bool> ans;
int kol = 0;
while (true) {
if (a == b) break;
reverse(b.begin(), b.end());
if (a == b) {
ans.push_back(false);
break;
}
reverse(b.begin(), b.end());
bool vozr = false, ub = false, r = false;
for (int i = 1; i < n; ++i) {
if (b[i] > b[i - 1]) vozr = true;
else if (b[i] < b[i - 1]) ub = true;
else r = true;
}
if (r || (vozr && ub)) {
cout << "IMPOSSIBLE";
return 0;
}
vector<int> c(n);
if (ub) {
ans.push_back(false);
reverse(b.begin(), b.end());
}
c[0] = b[0];
for (int i = 1; i < n; ++i) {
c[i] = b[i] - b[i - 1];
}
ans.push_back(true);
b = c;
++kol;
}
if (kol > 2e5) {
cout << "BIG\n" << kol;
} else {
cout << "SMALL\n" << ans.size() << "\n";
for (int i = ans.size() - 1; i >= 0; --i) {
if (ans[i]) cout << "P";
else cout << "R";
}
}
}
Thank you, everyone, for participating in the round! We hope you've raised your rating! And if you haven't, don't be sad, you'll do it!










Еще одно решение задачи E, которое мне кажется более простым, чем авторское.
Пусть все элементы из второй половины массива $$$=x$$$.
Пусть $$$s_k(i) = a_i + a_{i+1} + \ldots + a_{i+k-1}$$$.
Если существует такое $$$k$$$, что $$$k\le\tfrac{n}{2}$$$, то давайте посмотрим на такие сообщаемые числа: $$$s_k(i)$$$ и $$$s_k(i+k)$$$. Заметим, что если мы удвоим $$$k$$$, то $$$i$$$-е сообщаемое число будет равняться $$$s_{2k}(i) = s_k(i) + s_k(i+k)$$$. Так как $$$s_k(i)>0$$$ и $$$s_k(i+k)>0$$$, то $$$s_{2k}(i)>0$$$. То есть, после удвоения $$$k$$$, новое $$$k$$$ всё ещё будет подходить. Поэтому будем искать $$$k$$$, удовлетворяющее условию $$$k>\tfrac{n}{2}$$$.
Так как $$$k>\tfrac{n}{2}$$$, то для всех индексов $$$i$$$ должно выполняться $$$i+k>\tfrac{n}{2}$$$, то есть, все числа справа от отрезка $$$[i,\ \ldots,\ i+k-1]$$$ одинаковы и равны $$$x$$$.
Заметим, что если $$$x \ge 0$$$ и какой-то $$$k$$$ подходит, то подходит и $$$k+1$$$, потому что $$$s_{k+1}(i) = s_{k}(i) + x \ge s_{k} > 0$$$, то есть при $$$x \ge 0$$$ достаточно проверить случай $$$k = n$$$.
При $$$x < 0$$$ поступим следующим образом. Найдем для каждого $$$i$$$ такие числа $$$p$$$, что $$$s_p(i) > 0$$$. Заметим, что если $$$s_{p}(i) > 0$$$, то и $$$s_{p-1}(i) = s_{p}(i) + (-x) > s_{p}(i) > 0$$$, то есть, $$$p$$$ монотонно. Значит, разрешенные $$$p$$$ образуют отрезок от единицы до некоторого ограничения $$$t[i]$$$. В силу монотонности его можно узнать легко, используя массив префиксных сумм и бинарный поиск по $$$t[i]$$$ за $$$\mathcal{O}(\log{n})$$$, или использовать формулу (увеличение $$$p$$$ на 1 соответствует уменьшению суммы на $$$-x$$$) за $$$\mathcal{O}(1)$$$. Если для каких-то индексов никакой $$$p$$$ не подходит, будем считать $$$t[i] = 0$$$.
Итак, теперь заметим, что $$$k$$$ подходит тогда и только тогда, когда для всех $$$i$$$ от $$$0$$$ до $$$n - k$$$ выполняется $$$s_k(i) > 0$$$ или, что то же самое, $$$k \le t[i]$$$. Тогда можно просто перебрать $$$k$$$ от $$$n$$$ до нуля и проверять, что $$$k \le \min t[0,\ \ldots,\ n-k]$$$, поддерживая минимум. Если неравенство достигнуто — выводим $$$k$$$ как ответ. Если нет — выводим -1.
Итоговая асимптотика — $$$\mathcal{O}(n \log{n})$$$ или $$$\mathcal{O}(n)$$$, в зависимости от реализации подсчета $$$t[i]$$$.
Another solution to E which seems simpler to me.
Let's call the value of all elements in the second half of the array $$$x$$$.
Let $$$s_k(i) = a_i + a_{i+1} + \ldots + a_{i+k-1}$$$ — the reported incomes.
Pretend there exists such a $$$k$$$ that $$$k\le\tfrac{n}{2}$$$. Consider the following reported incomes: $$$s_k(i)$$$ и $$$s_k(i+k)$$$. Notice that if we double $$$k$$$, the $$$i$$$-th reported income will be equal to $$$s_{2k}(i) = s_k(i)+s_k(i+k)$$$. $$$s_k(i)>0$$$ and $$$s_k(i+k)>0$$$ imply $$$s_{2k}(i)>0$$$. It means that after doubling $$$k$$$, the new value will still be correct. So let's search for such $$$k$$$ that $$$k > \frac{n}{2}$$$.
As $$$k > \frac{n}{2}$$$, then $$$i + k > \frac{n}{2}$$$ holds for all $$$i$$$. It means that all numbers to the right of $$$[i,\ \ldots,\ i + k - 1]$$$ are equal to $$$x$$$.
Notice that if $$$x \ge 0$$$ and some $$$k$$$ is correct, then $$$k + 1$$$ is correct as well, because $$$s_{k+1}(i) = s_{k}(i) + x \ge s_k > 0$$$. So if $$$x \ge 0$$$, it's enough to check $$$k = n$$$.
If $$$x < 0$$$, we do the following. For all $$$i$$$ we find such numbers $$$p$$$ that $$$s_p(i) > 0$$$. Notice that if $$$s_p(i) > 0$$$, then $$$s_{p-1}(i) = s_p(i) + (-x) > s_p(i) > 0$$$. It means that if $$$p$$$ works, then $$$p-1$$$ works as well, so, actually $$$p$$$ can be any number from $$$1$$$ to some limit $$$t[i]$$$. It's easy to find $$$t[i]$$$ using prefix sums array and binary search in $$$\mathcal{O}(\log n)$$$, or use a formula (increasing $$$p$$$ by $$$1$$$ decreases the sum by $$$-x$$$) in $$$\mathcal{O}(1)$$$. If $$$s_p(i)$$$ doesn't hold for any $$$p$$$, assume $$$t[i] = 0$$$.
Finally, notice that $$$k$$$ is a correct answer if and only if $$$s_k(i) > 0$$$ holds for all $$$i$$$ from $$$0$$$ to $$$n-k$$$, or, using the precalculated array, $$$k \le t[i]$$$ for all $$$i$$$ from $$$0$$$ to $$$n-k$$$. It means we can just loop through $$$k$$$ from $$$n$$$ to zero and check if $$$k \le \min t[0,\ \ldots,\ n-k]$$$, maintining the current minimum. If the inequality holds, we output $$$k$$$ as an answer. If it doesn't hold for any $$$k$$$, we output $$$-1$$$.
The overall complexity is $$$\mathcal{O}(n \log n)$$$ or $$$\mathcal{O}(n)$$$, depending on $$$t[i]$$$ calculation implementation.
This is really cool. I tried establishing connections between k and k+1, never thought there would exist something between k and 2k.
Problem D Video editorial. Link
(https://codeforces.net/contest/1358/submission/81578791) Please explain where i am wrong.
use lower_bound instead of upper_bound. https://codeforces.net/contest/1358/submission/81589987
But what is wrong in using upperbound. Please explain.
just make int a[n+1] to long long int a[n+1]
thanks
use long long in place of int when defining a[n+1]. because the result get type cast to int instead of long long
thanks
Sir, your video tutorials and explanations are well understandable. Can you please make a video tutorial for problem E also :) Thanks in advance for your response. XD
For E why we cann't do k = n and check sum is positive or not? If positive then print k else -1
I can look like
-1 -1 -1 5 -1 -1 -1Another explanation for E:
Case 1: If total of all N elements is greater than 0, report N.
Case 2: If X >= 0, report -1. Because assume for the sake of contradiction some K works. Cover N with non-overlapping windows of size K until there are only X's remaining. Since each of these windows have positive sum and the uncovered X's are all >= 0, the total is greater than 0, which is a contradiction (since we would've returned in case 1 already)
Case 3: If X < 0, then K must be greater than N / 2 or else it will have a window of all X which are negative. This means the window must start in the front half and end in the second half. This leads to some easy formulas.
For some
K, for all0 <= i <= N - K, the following are equivalent:So track all the LHS you've seen so far for [0, i] and if the max is less than
prefix[N] + X * (N - i), you can returnN - ias your K.Python code: https://codeforces.net/contest/1358/submission/81555323
Why return N-i? Can you explain more detailedly?
Thanks I suddenly understand it !
Thanks for this explanation. I found it to be more practically reachable during a contest. Here's my C++ code: 81596230
Excellent solution!
Пока пытался разобраться, понял для себя более четкое объяснение:
1) С X >= 0 Выше уже было сказано много и все понятно.
2) Если X < 0, то будем искать K > N / 2(Очевидно, что K не может быть меньше, т.к. X < 0).
3) Начнем перебирать различные K, начиная с N. Тогда на первом шаге минимальная сумма на отрезке длинной K — это сумма всех элементов. Научимся за O(1), находить наименьшую сумму на отрезке длиной на 1 меньше. Возможны следующие варианты:
Минимум находится на новом отрезке, который заканчивается в позиции N — 1, т.е. на отрезке [N — K..N — 1], сумму на таких отрезках мы может быстро определять, заранее посчитав суффиксные суммы: suf[N — K].
Минимум находится на отрезке, который получается, если от отрезка с минимальной суммой для предыдущего K(который был на 1 больше) отрезать самый правый элемент(Отрезать левый элемент нет смысла, т.к. сумма гарантированно будет больше, чем при отсечении самого правого элемента. Доказательство достаточно тривиально.). Заметим, что, поскольку K > N / 2, то отрезанный элемент гарантированно равен X, и новая сумма равна: minSum — x
Таким образом, как только мы найдем состояние, в котором минимальная сумма для текущего K стала положительной — можно выводить ответ.
for(int i = 0; i < n; i++) { maxlimit[i] = (pref.rend() — upper_bound(pref.rbegin(), pref.rbegin() + (n + 1) / 2, (i == 0 ? 0 : pref[i — 1]))) — i; }
Hi purplesyringa I am not able to understand this code of yours. Could you please elaborate a bit?
upper_boundis a standard binary search function. However, it works only on increasing arrays, and that's not the case for us becausexis negative. There are two solutions to this problem: either reverse the array beforehand or use reverse iterators which makeupper_boundthink that the array is actually reversed. The first solution is used in the Python implementation, the second one is used in C++.So, the following codes are equivalent (I haven't compiled them though so there might be some minor issues):
Now to the code itself. I want to find such maximum $$$maxlimit[i]$$$ that $$$a[i] + \ldots + a[i + maxlimit[i] - 1] > 0$$$. We can rewrite this as $$$pref[i + maxlimit[i] - 1$$$ > pref[i — 1]$ (assuming $$$pref[-1] = 0$$$). So we just want to find the last position which is greater than some constant, which is equivalent to finding the first position which is greater than some constant in a reversed array, this is exactly what
upper_bounddoes.Thanks a lot. :)
How can you say that if p works then p-1 also works because there will an extra element s(p-1)(n-p).. So please can you explain that.
N = 5 A = {100,-1,-1} x = -1
So array becomes [100 -1 -1 -1 -1]
p=5 works but p-1=4 does not!!!
Notice that $$$k$$$ is some 'global' value, i.e. it's the same for all segments. But $$$p$$$ is 'local' to $$$i$$$, i.e. segments that start at different indicies may have different length. That's the case in your example: what exactly $$$p$$$ are you talking about? You say that $$$p=5$$$ works, but you didn't mention $$$i$$$, so I can just guess that you actually meant that $$$p=5$$$ works for $$$i=0$$$, i.e. the sum of $$$[100, -1, -1, -1, -1] > 0$$$ which is obviously true. Notice that $$$p=4$$$ works for i=0 too: sum of $$$[100, -1, -1, -1] > 0$$$. However, $$$p=4$$$ doesn't work for $$$i=0$$$.
Thanks for explaining it again.(Really appreciate that you responded to my doubt).
something similar i did too
purplesyringa what does maxLimit signify in your solution?
It's called $$$t[i]$$$ in the tutorial.
why dont we directly check for k=(n+1)/2 if x<=0, and k=n for x>0...??
Correct me if I am wrong.
It's enough to check that $$$k=n$$$ for $$$x>0$$$. But it's not enough to check $$$k=\lceil \frac{n}{2} \rceil$$$ for $$$x \le 0$$$, there's a countertest to this.
sp−1(i)=sp(i)+(−x)>sp(i)>0. It means that if p works, then p−1 works as well...(if p-1>=⌈n/2⌉). SO if at all if sp(i)>0, and p>⌈n/2⌉, this should also be true for p=⌈n/2⌉. Am I missing something..? Or please provide the counter testcase
Counter Testcase:
Consider the incomes array:
-1 2 2 -1 -1 -1Here sum of the array is
0For
K = 4, sum of each subarray is not>0For
K = 5, sum of each subarray is>0I could not understand the part of x<0. and whats t[i]. Can you please elaborate a little?
The simple case of $$$k=n$$$ only works for $$$x \ge 0$$$, so we have to handle $$$x < 0$$$ separately. We do that by calculating how much we can extend a segment starting in $$$i$$$ so that the sum of the segment $$$[i,\ \ldots,\ i + t[i] - 1]$$$ is positive. For example, for the array $$$[1, 2, 3, -2, -2, -2]$$$, $$$x$$$ equals $$$-2$$$, and $$$t$$$ equals $$$[5, 4, 2, 0, 0, 0]$$$.
great explanation..I understood till here ..now how to find ans from t[i]... logic to find ans from t[]..?
I can understand that from i till length t[i] we have positive sum.But this positive sum of length t[i] should be positive for all subarrays of length t[i].. how to check that within time constraints..as there may be many t[i]>0...?
can you please explain a little bit more? i appreciate in advance
Good problems, pathetic memes.
Need more memes in upcoming tutorials
Video Editorials for Problems C and D
For C, as given in the solution diagram, cant he go from 1 -> 3 -> 5 -> 8 -> 13 ?
We are trying to find different sums on way from 1 to 13. So the sum 1+3+5+8+13 has already been covered in 1 -> 2 ->5 ->9 ->13
B explanation ?
What exactly don't you understand? I might be able to help.
please can you explain problem D. I know that how every optimal segment ends in some end of month.But i am unable to implement,and can't understand where to use binary search or 2 pointer
Very good problems! As a participant, I really enjoyed solving this contest! Especially I liked memes in the problems
Video tutorial for today's C
Discord server
is it possible to solve C using nCk (binomial coefficient) ?
Do you mean the binomial coefficient?
Yes, I should've made it more clear.
There's no solution using $$$C_n^k$$$ that I know about.
You would get tle as far as I know because the limits are 1e9
I'm interested in learning the approach (if exists) regardless of the TLE, perhaps pre-calculating or DP can solve the TLE problem.
you can not solve though DP
technically you can solve with dp, because each previous case you add y (or x depending on if you're incrementing row or column), but in the end you can represent all cases with x*y+1
Yeah, I first built the dp matrix and then figured out that each row in this matrix is an Arithmetic Progression, hence the formula x*y+1 comes from there too!
i feel you bro i came up with a formula (n-m+2)!/((n-1)!*(m-1)!) only to get disappointed, although it ran through the test cases in questions.
but I am just thinking that why this formula isn't working here and was fetching a wrong answer in second pretest only. Can someone point out the issue with this formula when we have already taken care of the fact that calculating factorial doesn't leads to overflow.
Yeah about that!! Actually, the formula you calculated was for the total number of paths but in the question, we were asked to count only those paths whose sum's are different, i.e. in simple words we were not expected to count that path sum which we have already included. So, to do that we needed to optimise our solution which the author has achieved by calculating the subsequent path whose sum was increasing by 1 consecutively.
P.S: It would be better if go through this video tutorial. This guy has explained in a very intuitive way. If still not able to understand ping me personally.
Ok cool let's say I want to move from (1,2) to (4,5), can you give me an example of two different paths but producing the same sum.
i'm in love with those pictures
thanks <3
Anyone for TLE/WA uphacking on E? :)
81551641
Edit: Idea is — for x > 0 check k = n. For x <= 0 check shortest, longest, and maximum sum subarrays that contain all numbers in second half. If those 3 don't give a result check all possible lengths that have sum greater than any previous sum for intervals ending at n — 1.
Video Tutorial B:https://www.youtube.com/watch?v=OMRRHCeYsao
When you check the shorter solution of F first ..and wonder this is the shorter one
$$$O(N)$$$ solution for B (but it's barely within limits): 81499306
You iterate up to 10^5 for every test case regardless the given N for that test case so your solution is technically 10^5*10^4 for a test where every N=1
Yes, I realised. But after locking my solution. I was disgusted because I also came up with the editorial solution but thought this was better and just quickly submitted. The bright side is that it luckily passed and that now I know CF can handle about 5*10^8 operations in one second (although I won't be relying on it much in the future and will try to make better judgements about the solutions I implement). Good luck :)
For problem E, one could also eliminate some values of $$$k$$$ by randomly testing some starting points, then naively test each $$$k$$$ not eliminated: https://codeforces.net/contest/1358/submission/81552953
UPD: congrats to Kaban-5 for uphacking :)
we thought about it and it has some proofs (not strict) that there are no contrtests because second part has same numbers
I am still not getting (x2-x1)*(y2-y1) + 1 formula for problem C. like I understand row diff and col diff product gives a number of ways. but why we need + 1 at last. Can anyone explain? thanks in advance :)
The +1 at the end is to ensure the minimum path is included in the answer too.
plz someone explain this..why it is minimum and maximum sum path??
We will go through each diagonal exactly 1 time. The minimum on each diagonal is the upper right cell. And we can go through all of this cells. Similar for maximum.
@ilian04 could u plz clear meaning of "each diagonal" .plz because i am not getting what are u treying to convey by this word? there are just 2 diaginals ??
I was talking about this diagonals. First diagonal contains number 1. Second — 2 and 3. Third — 4, 5, and 6. Etc.
Thanks for this problem. I didn't get it in the contest but I enjoyed thinking about it afterwards.
I would suggest for next time to put some English text about how exactly the grid was generated (maybe some formal math stuff like $$$i+j$$$ uniquely defines a diagonal or whatever) instead of distracting stories about accounting and "Celex-2021".
In the contest I didn't make the trivial observation from the picture that each diagonal has increasing numbers (maybe that's my fault, and I'm supposed to infer that from the diagram with the color gradients).
But I was re-reading the problem statement multiple times looking for some explanation about how the grid was generated, and eventually guessed some random pattern about how the columns and rows have incrementally increasing numbers.
For Problem D, I believe you can do in O(n) time. You don't need to use Binary Search, can also use two pointers approach. 81531917
Yes of course, but author of problem thinks it is easier to understand binary search solution
Can you help me. When I am iterating from 1 to 2*n , I am getting WA verdict. https://codeforces.net/contest/1358/submission/81554812 But when I itaerate upto 2*n-1 I got AC verdict. https://codeforces.net/contest/1358/submission/81554853.
I am not able to figure out the issue.
Take a look at 81557505
When you run lower_bound or upper_bound, the your arrays / vectors need to be sorted in increasing order. If you have an extra 0 element at the end (or is otherwise unsorted), the binary search has undefined behaviour. I would guess both your submissions technically have undefined behaviour, but one of them just happens to pass.
Thanks for giving your time. Nice explanation also. Finally issue resolved
Thank you.
yeah i was thinking that as well, but the sliding window implementation was getting cancerous so i just gave up. i think author's solution is easier to implement but harder to understand, the 2 pointer method is more intuitive to come up with but holy hell, is it hard to implement (or i need more experience implementing weird 2 pointer problems)
It took me some time to understand how and why the nested loop while works. Great solution btw. Just please tell me your reasoning for making size of d as 2*n and the condition of first while loop.
Basically, you want d as 2*n because it the trip starts in month n, the trip might extend into the next year (eg: if a trip starts in year 1 month n-1, it could end in year 2 month 2) This is why d is the same array repeated twice. Basically, d stores the number of days of every month in year 1 and year 2.
Ptr2 tracks the month the trip ENDS. ptr2 <= 2n-1 means the trip must end in year 1 or year 2.
How do we know the trip cannot end in year 3 or later? Let's suppose the trip ends in year 3, month x. Since we know the trip must have only been under 1 year, then the trip must've started in year 2 month x or later. We know that an equivalent trip exists where you can start after year 1 month x, and end at year 2, month x.
Let me know if you have any questions about this explanation. Obviously not as rigorous as whatever the authors can come up with :)
Wow!!It's easy to understand!! :D
amazing tutorial crazyilian !!
Can anyone please check my solution out for problem B and let me know why I got TLE
time complexity of 'int a[200001]={0}' = 200001, and the number of test cases = 10000 so total complexity of your code = 10000 * 200001 > 2 seconds.
Wait...the editorial solution is O(N Log(N)) per test. which is 2e5*log(2e5). There are 1e5 testcases. That's 2e10*log(2e5) which is even greater!
It's guaranteed that the sum of $$$n$$$ of all tests is at most $$$2e5$$$, so it's actually $$$2e5 \cdot \log(2e5)$$$.
Got it. Thank you. I will read the question carefully from next time.
For D, you don't need binsearch. You can do a loop by which month you end on where you keep track of the the number of days left in the starting month and do a little casework on how many days you're advancing each loop. This is easier done going backwards.
Complexity: improved from $$$O(n \log n)$$$ to $$$O(n)$$$. Not that anybody really cares about that log factor.
81538134 — Here's my solution in weird, overabstracted Haskell. If, say, three people ask, I might write up a more readable C++ implementation.
EDIT: Apparently arthurg has already done that; refer to his post.
that is true. but solution with binary search is easier to understand and write, so we put it in tutorial
Ques A 81487617 Can anyone help I don't get what is difference between my solution and official solution.
official solution says m*n+1/2 whereas i wrote ceil((m*n)/2.0) is there any diff?
Your idea is correct, but you forgot that $$$ceil$$$ returns a float, not an integer. So if you try to output $$$1000000.0$$$, you'll actually get $$$1e+006$$$. You should round the float to integer (e.g. with
int(x+0.5)), or, even better, always use integers (e.g.(n*m+1)/2).Got it. thanks!
Make sure to read your testcase results. Testcase 3 says:
wrong output format Expected integer, but "1e+006" found
yeah my bad. will take care from now onwards.
Link
Can anyone tell me whats wrong in this logic?
In C I put in a redundant condition to check if x1<=x2 and y1<=y2. But this fails certain testcases. Why would that be can anyone help me with this? What could I be missing here. 81523820
if(x-a<0||y-a<0) there must be y-b<0, i think
well thats really stupid of me. howcome i mixed up a and b. damn that cost me a a couple of hundreds in rank
I would like to recommend everyone (or maybe those who are not into problem-setting) to read round log just to get an idea of how much efforts go down in making a good quality official Codeforces round.
Am I the only one who solved D without noticing that the end of the vacation coincides with the end of some month? 81543406
same
Please ,Remove the picture of problem D .
its look like ……….
Very good explanation for problem C.
Memes in problem statement would have been nice!
thanks
Thank you, that explains why I found it so hard.
How does https://codeforces.net/contest/1358/submission/81520389 exceed time limit? since max of a is 2*10^5 or just O(2n) how does it exceed TL?? It passed the pretests during the contest, but i saw that after the contest i got it wrong :(
The for loop runs up to 2e5 times, for every one of the 10000 testcases.
I solved D using the idea that optimal answer coincides with end of a month. But now I have an issue. Let's say after concatenating 2 arrays to consider the whole array as one year we get 1 2 1 2 1 2 1 2 1 2 1 2 (insert more 1 2 over here)... 1 2 1 2 3 4 5 1 2 3 4 1 2 3 1 2 1 2 3 4 1 2 3 4. Now let's say we consider the segment 1 2 3 4 1 2 3 1 2 1 2 3 4 1 2 3 4 (the segment after 5). It ends at 4 right. So if we move this to left by 1 the answer should decrease because then it would not be end of an array(month). But when we shift it to left by 1 we subtract 4 and add 5(see in original array.. 5 is before 1) so in total we end up adding 1 to the answer. So how to we prove that optimal answer should have end of a month when this is failing over here.
Also, one of the optimal answers will 2 3 4 5 1 2 3 4 1 2 3 1 2 1 2 3 4
You're right, we can shift it to the left by 1 and increase the answer. However, you can continue shifting it to the left and get 2 3 4 5 1 2 3 4 1 2 3 1 2 1 2 3 4, which does end at the end of the month.
So basically we can't just prove it by using one segments right. It's kind of ternary search. Got confused because in editorial you explain using just one segment and shift it. That is not always the case right? We have to show that it will decrease and increase both and form some sort of concave function. Am I missing something? Basically I want to know that if I came up with that case during the contest how(how to prove it then) and why would I proceed with the same approach of optimal answer ending in a month?
Maybe you missed that we see rightmost optimal segment in proof?
I'm sorry but what difference does that make?
If we shift segment to right, sum will strictly decrease
Yes that's what I exactly get from the editorial that we can't shift rightmost segment to further right. But the thing I'm not getting is that how to prove that it'll end up at the end of some month while shifting to the left? How does the editorial prove that fact?
It is proved by contradiction,if this statement (about end of the month) not true we have contradiction, so that's impossible, and statement is true.... I can't explain it clearly
I can't understand it clearly either. Contradiction is shifting it to left by 1 thus increasing the answer. But it's not proving that it'll stop at some endpoint. Maybe I'm missing something but I'm not at all clear with that. Because otherwise if I make a statement that the answer will not lie at the endpoint and then consider a segment like above and prove by contradiction by the same test case above then I don't think that proves anything. Please tell me what am I missing.
In editorial there is a proof, that shows we can shift segment only left or right only 1 time, and it will be incorrect. We don't shift it infinitely,only one time. Please reread the editorial, I am really sorry, that I can't explain it :(
Is it a problem — the last line in Excel?
Ctrl+↓, and here it is!For the last column, use
Ctrl+→.YOU are hired!
This man was Albert Einstein.
I just saw it in OpenOffice, and in Excel it suddenly works too. By the way, the tables in OpenOffice are much smaller.
Typical IT lesson in the school...
Kudos codeforces team and the authors very fast tutorial and the rating was also updated very soon. I don't think both of these took place so fast ever. codeforces gets better every day.
thank you @MikeMirzayanov.
I think, authors and coordinator responsible for fast publishing
I'm having a hard time understanding test case #14 for problem E
We'll need 1348046 ops to pref() 1 1 1 to
and 1 op of reverse to make it to
and 1 op of pref():
and 1 op of reverse() to be the target array. How come the answer be 1348047?
Do you mean F? And in that case, you have to print the number of
prefoperations, not the total.Thanks so much! That's so tricky.
Why isn't Ternary search applicable in D? Isn't the function a point wise supremum of affine and hence convex functions?
Those grannies are yelling "Go Corona Go"
D can also be solved in O(n)
Link to my submission:
https://codeforces.net/contest/1358/submission/81557479
please explain the logic also..
2 pointers instead of binary search
Somewhat similar to Circular Kadane's Algorithm. Just instead of when sum become negative resetting to zero, remove that value of last month added if your sum exceeds x... kind of two pointer approach as the guy below has mentioned..
anyone plz help me to understand problem B ? thanks
For problem E I wrote a code which got WA in test 58 but I will share my idea : as mentioned in the editorial if a solution exists so it is >n/2 let's calculate the prefix array sum since in the second half of the array we have same values so we have two cases: either the accumulative sum will increase if value in second hlaf called x is greater than 0 or it will decrease so in both cases the array accumulative sum will either have a suffix(maybe empty) containing only strictly positive values or negative ones depending on the starting index here is my submission
Here i have something about problem C, which i was trying to solve but couldn't. First $$$x$$$ is for row and $$$y$$$ is for column.
A path can be seen as this, a binary sequence of length $$$x2-x1+y2-y1$$$, with number of ones equal to $$$x2-x1$$$. How this happens? oky see, when we want to choose a path, we are now in cell $$$[x1,\,y1]$$$ we can go down or right, if we go down then the head(the number on the cell we are, comparing to the number on the last cell we were) will be increased by $$$x+y+1$$$, and if we go right then the head will increase by $$$x+y$$$ so the difference between them is 1, and so it also applies to next numbers. So we have a sequence of ones and zeroes of length $$$x2-x1+y2-y1$$$ with $$$x2-x1$$$ ones(number of times we go down) and $$$y2-y1$$$ zeroes(number of times we go right).
Now the magic begins, two path's sums are different if and only if the sum of suffix sums of they're sequences are different. And so the answer to the problem is the number of different sum of suffix sums a binary sequences of length $$$x2-x1+y2-y1$$$ with $$$x2-x1$$$ ones can get, YAY, we turned our D1A problem to a literally harder problem. Please let me know if you could solve it that way.
Actually i did C the way you described above.
But after noticing, that when we go to the right, number in the cell will increase by x + y, and when we go down it will increase by x + y + 1. Due to one to one correspondence i replaced it with the sequence we would get, if number in the cell increased by 1 when we go down and stayed unchanged after going to the right.We will concider 2 new sequences distinct if their sums are different. Lets concider a path: once we go down the number in the cell increases, and this 1 will be added up to each cell in path, starting from this cell. So we can calculate the sum of the elements of the new sequence as a sum of l for all l, where l is the serial number(calculating from the end) of the turn we go down from in path. 1 <= l <= (x2 — x1 + y2 — y1) . So our task is reduced to finding number of different sums of x2 — x1 numbers(number of times we go down), where numbers are distinct natural numbers from the segment [1; (x2 — x1 + y2 — y1)]. The smallest possible sum is S1 = 1 + 2 + ... + (x2 — x1) and the largest possible sum is S2 = (y2 — y1 + x2 — x1) + (y2 — y1 + x2 — x1 — 1) + (y2 — y + x2 — x1 — 2) + ... + (y2 — y1 — 1). It is obvious that any sum between is reachable, it means that number of distinct sums is equal to S2 — S1 + 1. Using well known fromulas of summation , we get that answer is (x2 — x1)(y2 — y1) + 1.
The problem you proposed could be solved similarly. Actually, the sum of suffix sums of your sequence is equal to the sum of elements of my new sequence(see above). (Because if we replace numbers in your sequnce by their suffix sums, we get my new sequence. And new criteria of distinctivity of sequences would be distinctivity of their sums of elements)
Nice, i wanted some math/combinatorics solution for it, but yes the same idea as editorial can be used here, thank you.
Another way to visualize the solution to C :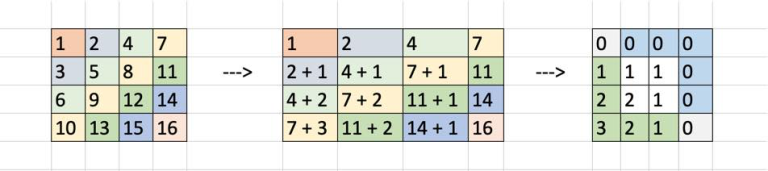
The difference between max sum and min sum is shown in the last matrix. This difference is sum(green) — sum(blue). Hence total number of sums between the two is (max_sum — min_sum + 1) = 10 for this 4x4 example.
LOL i'm glad that someone else saw it like that, i just needed to find a reliable way to actually calculate it so i wrote out each case on a grid and guessed the answer once i saw the x*y+1 pattern
Yea it's one of those problems where people could sort of get away with a lucky guess, I suppose. It was certainly very time consuming to prove during the contest. I think a better strategy for such problems would be to just guess 1-2 times based on intuition, before going the long route of proving the solution..
I also solved the same way.
if it is a rectangle instead of a square?
Take a 3x4 :
Range of sums is from 0 to 6. Answer: is calculated as the (sum of numbers along green path) — (sum of numbers along blue path) + 1 :
Basically, it doesn't matter what numbers are in the rectangle (i.e. x1, x2, y1, y2 are irrelevant. All that matters is x2-x1 and y2-y1). All 3x4 rectangles boil down to the numbers in the third diagram. The path with the smallest sum runs along the blue cells (right on row 1 and then down on column n) and the path with the largest sum runs along the green cells (down on column 1 and then right on row m)
thanks bro for this great visualization but sorry that I am still unable to get how does that make us reach to (c — a) * (d — b) result
The visualization was actually more of the proof and how to think about the solution.
To get the m * n formula, consider that you have a 2x4 matrix (2 rows, 4 columns), so you can move down 2 times and right 4 times. The smallest sum path is: DDRRRR and largest sum path is RRRRDD. Every other path in between needs to be included. So here are all the paths (from smallest to largest) :
This comes to:
(number of downs) * (number of rights) + 1= 9 for this 2x4 example.I had solved it using a different method by counting the number of diagonals and adding their "lengths" (as each diagonal "length" represents the difference between the smallest and largest elements on that diagonal). So the visualization was more pertinent to that solution.
huge thanks bro..i understood
crazyilian The solution to problem C: Celex Update contains a (q--) instead of a (t--).
So is this balanced ? I mean no graphs and no data structures ?
Don't forget that 13 problems were redjected
typo in D
di=a1(a1+z)2+...+ai(ai+1)2that must be a1(a1+1) crazyilianhttps://codeforces.net/contest/1358/submission/81540947 this o(n^2) solution passed D
Problem F can be solved in $$$O(\log^2 C \cdot n \cdot min(n, t))$$$.
It is possible to show that after applying $$$k$$$ operations of "rollback" the elements of $$$b$$$ will change as follows:
$$$b_{i} = \sum_{j=0}^{min(i, k)}(-1)^{j} \cdot \binom{k}{j} \cdot b_{i-j}$$$
This calculation takes $$$O(n \cdot min(n, k))$$$ time.
Instead of applying a list of rollback operations in a row one-by-one, I want to make a binsearch to calculate the maximal number of operations I can apply.
In details, these two conditions must hold if it's possible to apply some number of rollbacks:
All elements of the resulting array must be positive
The sum of all elements must be not less than the sum of elements in $$$a$$$.
It can be proven that while applying rollbacks if at some point a negative element appears in an array, then it will stay there forever.
So, this solution works in $$$O(\log C \cdot n \cdot min(n, t) \cdot R)$$$, where $$$R$$$ — number of reverses in the optimal answer.
If $$$n = 2$$$, $$$R = O(\log C)$$$, hence it holds for the bigger values of $$$n$$$.
In order to overcome overflow problems, the binsearch can work similarly to binary lifting (firstly, we increase the step by $$$1$$$, $$$2$$$, $$$4$$$, ... and then decrease it in the reverse order).
This solution doesn't require separate consideration of the case $$$n = 2$$$.
My code: 81528455
E also can be solved using min segment tree with push updates. As In solution k >= n/2, we iterate k from n/2 to n,add x on prefix 0...n-k and check if it > 0 81558894
D can be solved by:
81566497
C. There are six possible unique sums(on the diagram). But why is the answer 5?(2*2+1)
take test case (1,1) and (3,3), down right right down sum = right down down right sum even though they are two different paths.
Can someone pls explain how is Problem C different from the standard
Find number of ways to reach one point from another in a gridwhich has an answer of (M+N)!/(M)! (N)! after shifting x1, y1, to origin?take test case (1,1) (3,3) for example
if you go: right down down right and down right right down, they result in the same sum. thus, you cannot count that.
instead, take the minimum sum possible (go all right then all down), and then the maximum sum (all down then all right) and subtract them. i wrote out all the test cases (represented as xdelta and ydelta) and guessed that it was xdelta * ydelta after seeing the pattern
Great Contest!
Why are we not solving problem C in this way Let D1=x1-x2 D2=y1-y2 Ans would be arrangement of D1 no of x and D2 no of y So why we not directly write the ways of d1 x and d2 y Eg D1 is 3x-xxx and D2 is yyy ie 3y So ans is (3+3)! and also there are repeatitions of x and y so (3+3)!/3!3!
you are solving for the no of distinct paths between starting and ending points but not for the distinct sum paths and also you cant find the factorial of 10^9 without a mod
I have a bit shorter solution for Problem F. The idea is approximately the same as the tutorial. I notice that when $$$n>2$$$, n*t is always smaller than 10^8, so we can implement the $$$n>2$$$ parts together. In my code, I just simulate the first 2000000 'P' operations regardless of n, which I think makes my code neater. Then I deal with n=2 specifically.
Submission 81693390
Please hide the code inside spoiler tag.
Thanks for your advice ^_^
HackerMonk Can you just add comments in your code 81570956 so it is more understandable, since your code seems to be much simpler and nice, in comparison to the editorial one.
No problem, I just updated my comments. I'm glad if it helps. ^_^
Thanks a lot for sharing your experience as first-time problemsetters! I'm currently waiting on a proposal I made, so your story helps me know more or less what to expect from the coordinator (patience, more than anything :P). This is specially cool since I've never seen anyone write about their experience with the coordinator or with Mike, they're kind of an unspoken secret throughout setters, so thanks for breaking the ice on that.
For problem C, I calculated the actual minimum and maximum sum possible and got TLE for using big integer in C++. My solution This might help in future in such diagonal filling problems if constraints are a little lower. P.S. — I 90% sure my solution gives the correct answer. Can someone give me assurance of 100% or tell me it is wrong for some cases?
how is (c — a) * (d — b) giving unique paths in problem C please explain? I think I am a bit weak at p&c so explain in easy language please
Ok let me explain this to u ... may it helps u!! See first of all u go through the first row up to the last coloum (that path of minimum sum). Now all u need to do is that go up to the second last coloumn and move down and go right again and u will see that u are matching with the same path. Now take the same turn for third last column(go down) and then go right staight and then u will be in the last coloumn matched up with the initial path...u will better find this in the editorial .. by doing this u can see that every time u are making change in the (y2 — y1) coloumn and reaching the the last coloumn by going straing right. The same thing can be done for the rows also u will make changes in (x2 — x1) rows. so the number of path would by the multiplication of (x2 — x1) * (y2 — y1) + 1. NOw why +1? because we are merging into the path of minimum sum and we calculated all possible path to merge into it but we haven't count the original path (path of minimum sum) so +1 is for that. EDIT1 — sorry for any grammatical mistake. EDIT2 — see something else if u don't find proper help by this THANKS U
That's an interesting editorial and well explained
I used 2 pointer for D but it gives WA because of overflow in C++, i tried unsigned long long too 81577649
I think it's overflow because my exactly same python sol is getting AC 81577330.
Can anyone plz tell me where I can improve?
I think we could make memes out of these memes.
amazing contest! questions were interesting to solve
I just FUCKING don't understand what does the picture mean in D.
funny mud pee
+1
I declare that it's only my personal attitude.
Someone is saving others' lives, while someone is just slandering.
I think that controversial pictures like this shouldn't appear
It seems that a large number of people disagree with what Chinese people have done.
清者自清
Language...It's true that this picture makes an insulting presence, but that f-word does not solve the problem. Shouldn't we just contact the authors for a declarement?
+1
D in O(N): I know I'm dumb, Can someone please tell me the problem with my lame attempt to solve D.
https://codeforces.net/contest/1358/submission/81573541
Could somebody please tell why it's down voted so much?
NOW ITS SUBMITTED https://codeforces.net/contest/1358/submission/81641980
nmsl
How made winds, I love it :)
Never mind the scandal and liber❥❥❥❥❥
I just like the spirit of War Wolf. Although I am a Japanese, I still learned a lot from this man. I hope you can spread this kind of ideology globally, so that all human beings can be saved from the imperialism! China No.1!
Nah ur not...
I would like to thank 300iq for removing the pictures.
They should write a blog apologizing for it.
Don't be so angry.Maybe they just want to joke.I think removing it is proper enough.
犯我中华者,虽远必诛!
Awww man, don't be too serious about this, it'll only intensify the conflict.
Indifferently insisting on presenting the "joke" anyway is not.
A blog might be too much but at least consider the feelings of the masses who have suffered. Humankind should be kind. Humankind needs to unite in the face of the pandemic.
I agree that they shouldn't post that picture.
But I am not defending for them. I mean, some people aren't sensitive enough that they cannot realize how serious this problem is. Removing the picture and apologizing is necessary, but being much angrier than usual can't solve anything.
Yeah, I agree. It's much better to suggest our opinions in a calm way instead of propogating meaningless slogans.
indeed
I'm having some weird problems with overflow at problem D (I'm new at C++). Can someone take a look? (https://codeforces.net/contest/1358/submission/81592636)
Should have made x long long... Java is way better for debugging lol.
At problem D at test 12, my program doesn't for some reason take the correct numbers of days as input, instead it takes just straight 0s... (https://codeforces.net/contest/1358/submission/81596666). Does anyone have any idea what could it be, since the program surprisingly works for earlier tests? I'm new to c++.
Should have made x long long... Java is way better for debugging lol.
$$$t = O(\sqrt[n - 1]{C(n - 1)!})$$$. What? Using Stirling formula we can estimate, that $$$\sqrt[n]{n!} \approx \frac ne$$$, so whole solution will be $$$O(n^2)$$$
If we apply operation R $$$t$$$ times on array $$$[1, 1, \ldots 1]$$$ of length $$$n$$$ we get that last element equals $$${n + t - 1 \choose n - 1}$$$. I guess you used bound $$${n \choose k} \leq \frac{n^k}{k!}$$$, which works fine if $$$k$$$ is way smaller than $$$n$$$, but is an insane overestimate in our case, when $$$n = 2\cdot 10^5$$$, $$$t = 3$$$
In fact the task was harded before (the limit was $$$10^{18}$$$, not $$$10^{12}$$$), but almost no one solved it so $$$C$$$ was reduced. So we did come up with $$$C_{n+t-1}^{n-1}$$$ which was used in the solution of the harder task. You're right, the complexity is definitely overestimated. We had a smaller bound before which worked well but we didn't have a solid proof, so we used this one. I'll try to prove it and fix the issue.
Is it really that harder? For $$$n \geq 4$$$ largest number of steps before exceeding $$$10^{18}$$$ is $$$1817118$$$, which should be small enough. The only case left is $$$n = 3$$$. Within $$$k$$$ steps of R operations $$$[a, b, c]$$$ transforms into $$$[a', b', c'] = [a, b + ka, c + kb + \frac{k(k + 1)}{2}a]$$$.
Solving for $$$a, b, c$$$ in terms of $$$a', b', c'$$$ (or substituting $$$-k$$$ for $$$k$$$) we get, that if we run $$$k$$$ reverse operations on $$$[a, b, c]$$$ we get $$$[a, b - ka, c - kb + \frac{k(k - 1)}{2}a]$$$. For the second value we can do basic binary search to find largest $$$k$$$ for which it is positive. Third is bitonic in terms of $$$k$$$, so to find where it is positive we can for example use ternary search to find minimum, and then on interval from $$$0$$$ to that maximal value binary search where it is positive (or use quadratic formula to find this segment).
testers said that is "hard realization" and we made problem simplier
I wonder what was the original version of the city where Coronavirus-chan lives in.
It was "Nahuw" (it isn't joke). In Russian, it sounds like a swear word, and even "Wuhan" in reverse)
I can't imagine what if it weren't 300iq that coordinated the round.
Will you feel good if someone else "just made some cool memes" about Chernobyl?
Hey, why isn't the path 1+3+5+8+13 taken into consideration in Problem C ?
Because it has the same sum as the path 1+2+5+9+13.
In case anyone need Detail explanation for D Here
I'm not sure whether my solution to F is shorter...
Cuz it's a different way of presenting.
You can use spoiler to show your code better.
owo
Ah, yes, thanks.
Nice!!
https://codeforces.net/contest/1358/submission/81676727 my code is shorter, because most logic is consistant.
orz. You solved it in the contest.
Nah, urs' better. stO qfhy Orz.
I realised that my proof of D was wrong. The proof in the editorial is very nice indeed!
In my view, codeforces is a great training platform with high quality problems. Please do not make it politicized.
Thank 300iq for his wise decision!
Can someone please explain the two pointer approach for problem D?
This code might be helpful. https://codeforces.net/contest/1358/submission/81562536
I can't seem to find the error in my solution so if anyone can spot it: https://codeforces.net/contest/1358/submission/81631720
Why downvotes?
It insulted those who had died fighting a novel coronavirus !
(I'm Come from Wuhan :( )
Can someone tell me what is the time complexity of my code? https://codeforces.net/contest/1358/submission/81649608
Great work guys, thanks for the contest. It requires a lot of work to host a contests on Codeforces. Problems were really interesting, had fun solving it.
It's sad that editorial is being downvoted so badly after such a hard work by problem setters,testers and codeforces. Hope it gets upvoted!! It motivates problem setters, we get more great contests :)
Yet another explanation of E:
Read proof that k > n/2 from editorial (it's nice and simple)
I check every k from n/2+n%2 to n and return the first good k.
I always start at the end with the last k characters. Let's take a look (for simplicity assume that n is even):
t[1],t[2],..,t[n-k-1], t[n-k], base
base = t[n-k+1],..,t[n/2],x,..,x
The base is initially at the end and I will move it to the left. Let's look at the first 2 shifts:
t[1],t[2],..,t[n-k-1], base1, x
t[1],t[2],..,t[n-k-2], base2, x, x
sum(base1) = sum(base) + (t[n-k]-x)
sum(base2) = sum(base) + (t[n-k]-x) + (t[n-k-1]-x)
and so on. We see that the shift by l positions equals to adding a continuous subarray of values: (t[n-k]-x) +..+(t[n-k-l+1]-x) to sum of our initial base. In order to find the worst segment, we should find a minimum continuous subarray ending at an appropriate position (it is a standard subproblem — here we allow empty array).
So we can check if the k is ok by if(sum(base)+worst_subarray[n-k] > 0) in O(1) and we run it for all candidates.
So, you wrote that we need to find the continuous subarray
(t[n-k]-x) +..+(t[n-k-l+1]-x). I just wanted to confirm that will the worst_segment be of sizel? If yes, then you also wrote that to find the worst segment, we have to find the minimum continuous subarray ending at an appropriate position(doesn't this take O(n) because we have to iterate by sliding window of sizelto make sure that size of each segment island then take the one that gives minimum segment sum? And if this really takes O(n) then we do this for every possible k fromn/2+n%2tonand later return the first good k.)Can I get the link to the above explanation too?
Thanx in advance.
l is the size of the shift — from the end, we shift l times to the left. The size of the window is k.
The shift of the window with size k by l positions to the left can be expressed as (t[n-k]-x) + (t[n-k-1]-x) +..+ (t[n-k-l+1]-x) + base. In order to find the worst shift (the position of the window, with the smallest sum) we need to find the smallest continuous subarray ending at n-k. We can pre-compute these values and for each k we find the position of the window in O(1).
ok got you. So, isn't this quite brute force, because we are doing this for k between
n/2 to nand for each k we are shifting the window by a total of l positions so isn't the total time complexity equal to O(n/2*l). Can you help in finding theeffectivetime complexity of O(n/2*l). I don't know why I get the feeling that this is O(n*n). If so, can you correct me?You check each k in O(1). You find the worst shift by adding the minimum continuous subarray (each shift is represented by the continuous subarray, so the worst one is the minimum subarray). You can check my submission.
bad memes
I wonder whether the writers of this round are idiots.
I think the tutorial of problem E is too tedious...
In E's editorial there are some inconsistent statements like "Notice that the minimum reported income (some number from $$$s$$$) doesn't depend on the first element of $$$p$$$", while next sentence says explicitly that if we change $$$p_1$$$ then all of the $$$s_i$$$ would change as well. So these $$$s_i$$$ do actually depend on $$$p_1$$$ while what is meant for $$$s_i$$$ is that its $$$\sum_{j=2}^{i} p_j$$$ part would never change.
Anyways, do you have some easier solution/explanation?
In my opinion, the first step is the key of this problem and its proof is given in the tutorial.
Then let K=(n/2)+1 which is the minimum possible k, and then we let b[] = {s_1, s_2, ... , s_{n-k+1}} (s_i means a_i+a_{i+1}+...+a_{i+k-1}). And this can be calculated in O(n).
Consider how b[] changes when K=K+1. It is obvious that b[] changes into b'[] = {s_1+x, s_2+x, ... , s_{n-k}+x} (or we can say we add b[] by x and remove the last element). Notice that if min_element(b[])>0 we get a valid answer, than we can solve this problem without the tedious mathematical derivation. And I think it is much more intuitive maybe?
My code: https://codeforces.net/contest/1358/submission/81881217
nice !! much intuitive as compared to all other solutions.
Some did it by Segment trees, can you explain how can we do it using segment trees?
I just tried to use lower_bound instead of upper_bound in problem D. Still it got accepted. Can anyone explain the reason? Thanks in advance!! Submission--> 81893828
r
O(logn) solution for B
104247218 If you want explaination comment it and I will