vrkorat211's blog

Maximum Path sum in tree
By vrkorat211, history, 4 years ago, In English

Question asked in Google online coding challenge on 22nd AUG, 2020.

Please help me with this question.

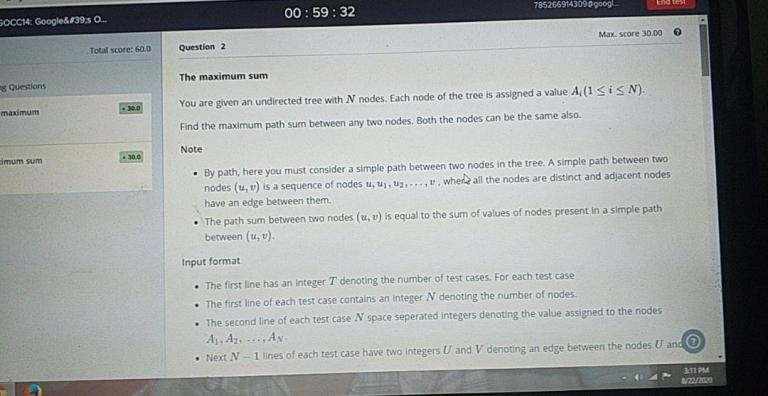
You are given a tree with N nodes numbered 1 to N. Each node is having weight Ai. (1 <= i <= N)

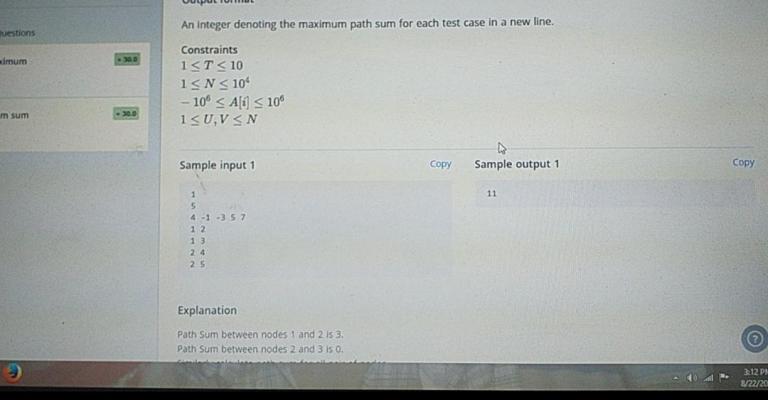
Find the maximum path sum between any two node u and v of the tree. Return the maximum path sum value. constraints:

1 <= T <= 10
1 <= N <= 1e4
-1e6 <= Ai <= +1e6

Example:

  • Vote: I like it
  • -16
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A simple DP should work ig.

→ Reply
»
4 years ago, # |
← Rev. 6   Vote: I like it 0 Vote: I do not like it

It can be solved using dynamic programming on trees. Refer the following link to find maximum path sum of a binary tree : https://www.geeksforgeeks.org/find-maximum-path-sum-in-a-binary-tree/

For a normal tree, we just need a little bit of manipulation,

Let $$$dp1[i]$$$=maximum path only includes node 'i', $$$dp2[i]$$$=maximum path that passes through node 'i' and one of its children. $$$dp3[i]$$$=maximum path that passes through node 'i' and two of its children. Now, $$$dp1[i]=a[i]$$$

$$$dp2[i]=a[i] + max(dp1[v1],dp2[v1],.............dp1[vk],dp2[vk]) $$$,

where $$$(v1,v2,....vk)$$$ are children of node "i".

Similarly, $$$dp3[i]$$$ can be calculated.

Final answer is maximum of all the $$$dps$$$ from $$$i=1$$$ to $$$N$$$

Time Complexity : $$$O(N)$$$

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I'm not exactly sure but we can flat tree and at in time value will be a[i] and at out time value will be -a[i].Now we can just apply kadane's algorithm to find largest sum,but starting point should be in point only and ending point is also in point,also starting point and ending points should be different,by different I mean that we should select at least two points.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it 
#pragma GCC optimize("Ofast")
#pragma GCC target("avx,avx2,fma")
#pragma GCC optimization ("unroll-loops")

#include <bits/stdc++.h>
using namespace std;

vector<int>a, sz;
map<int, vector<int>>th;
int ans   = 0;
void dfs(int u, int p = -1) {
	int cool = 0 ;
	int tot1 = 0 , tot2 = 0 ;
	for (auto v : th[u]) {
		if (v == p)continue;
		dfs(v, u);
		if (a[v] > tot1) {
			tot2 = tot1;
			tot1 = a[v];
		} else {
			tot2 = max(tot2, a[v]);
		}
		cool = max(cool, a[v]);
	}
	int tot = tot1 + tot2;
	ans = max(ans, a[u] + tot);
	a[u] = a[u] + cool;

}
int32_t main() {
	ios_base::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);
#ifndef ONLINE_JUDGE
	freopen("input.txt", "r", stdin);
	freopen("a.txt", "w", stdout);
#endif
	int t;
	cin >> t;
	while (t--) {
		int n;
		ans = INT_MIN;
		cin >> n;
		a = sz = vector<int>(n, 0);
		for (int i = 0; i < n; i++) {
			cin >> a[i];
		}
		th.clear();
		int e = n - 1;
		while (e--) {
			int u, v;
			cin >> u >> v;
			u--, v--;
			th[u].push_back(v);
			th[v].push_back(u);
		}
		dfs(0);
		cout << ans << "\n";
	}
	return 0;
}

this was my working submission for this question

→ Reply