Problem A is developed by mejiamejia.
1733A - Consecutive Sum
$$$i$$$-th element moves only to $$$(i + xk)$$$-th position ($$$x$$$ is integer).
We cannot select $$$a_i$$$ and $$$a_{i + xk}$$$ simultaneously. In other words, if we can swap $$$a_i$$$ and $$$a_j$$$, we cannot select $$$a_i$$$ and $$$a_j$$$ simultaneously.
Among all elements $$$a_{i + xk}$$$ for each $$$i$$$ ($$$1 \le i \le k$$$), only one element is selected.
For each index $$$i$$$ ($$$k + 1 \le i \le n$$$), there is exactly one element among $$$a_1$$$ to $$$a_k$$$, which can swap with $$$a_i$$$. If $$$a_i$$$ is greater than that element, swap them. This process perform the operation at most $$$n - k$$$ times. After performing operations, select $$$a_1$$$ to $$$a_k$$$. This is the maximum score we can get.
After performing all operations, select $$$p$$$ consecutive elements. $$$p$$$ can be different from $$$k$$$. Find the maximum score.
1733B - Rule of League
Because one of player $$$1$$$ and player $$$2$$$ win $$$0$$$ games and the other win at least $$$1$$$ game, $$$\min(x, y) = 0$$$ and $$$\max(x, y) > 0$$$ must be true in order to generate a valid result.
There are one winner and one loser for every match. So the sum of winning count and the sum of losing count are same.
The sum of winning count is a multiple of $$$\max(x, y)$$$. Therefore, the sum of losing count is also a multiple of $$$\max(x, y)$$$.
(The sum of losing count) equals to $$$n - 1$$$. So $$$n - 1$$$ is a multiple of $$$\max(x, y)$$$ if there is a valid result.
According to hints, $$$\min(x, y) = 0$$$ and $$$\max(x, y) > 0$$$ and $$$(n - 1) \,\bmod\, \max(x, y) = 0$$$ holds in order to generate a valid result. If so, player $$$1$$$ and player $$$2$$$ would play first. Let's consider player $$$2$$$ wins. Then player $$$2$$$ should win $$$\max(x, y)$$$ games, and loses to player $$$\max(x, y) + 2$$$. Likewise, player $$$\max(x, y) + 2$$$ wins $$$\max(x, y)$$$ games and loses to player $$$2 \cdot \max(x, y) + 2$$$. Construct the remaining result in the same way.
Expand $$$x$$$, $$$y$$$ to $$$x$$$, $$$y$$$, $$$z$$$?
1733C - Parity Shuffle Sorting
If all elements are equal, that array is also non-decreasing.
For each operation, one element is changed. Because we have to use at most $$$n$$$ operations, an element change occurs at most $$$n$$$ times. Considering that the initial array can be decreasing, at least $$$n - 1$$$ operations can be needed in some cases.
If $$$n = 1$$$, do nothing.
Otherwise, select indices $$$1$$$ and $$$n$$$ to make $$$a_1$$$ equal to $$$a_n$$$ first. After that, for each element $$$a_i$$$ ($$$2 \le i < n$$$), select indices $$$1$$$ and $$$i$$$ if $$$a_1 + a_i$$$ is odd, and select indices $$$i$$$ and $$$n$$$ otherwise. This process requires $$$n - 1$$$ operations and make all elements equal, which is also non-decreasing.
Find the minimum number of operations?
1733D1 - Zero-One (Easy Version)
Consider $$$c$$$ is another binary string, in which $$$c_i = a_i \oplus b_i$$$. We have to make $$$c$$$ equal to $$$000 \ldots 000$$$ using the operation.
Because the operation does not change the parity of the number of $$$1$$$ in $$$c$$$, the answer is $$$-1$$$ if $$$c$$$ has odd number of $$$1$$$.
If the number of $$$1$$$ in $$$c$$$ is $$$d$$$ (now assume that $$$d$$$ is even), at least $$$\frac{d}{2}$$$ operations are needed. So total cost would be at least $$$\frac{d}{2} \times y$$$.
One $$$x$$$-cost operation can be replaced with two $$$y$$$-cost operations.
Consider another binary string $$$c$$$, in which $$$c_i = a_i \oplus b_i$$$ ($$$1 \le i \le n$$$). So doing an operation means selecting two indices of $$$c$$$ and flipping them. Also, let's define $$$d$$$ is the number of $$$1$$$ in $$$c$$$. Because the parity of $$$d$$$ never changes, the answer is $$$-1$$$ if $$$d$$$ is odd.
If $$$d$$$ is even, classify the cases:
$$$[1]$$$ If $$$d = 2$$$ and two $$$1$$$-s are adjacent, the answer is $$$\min(x, 2y)$$$. Because $$$n \ge 5$$$ holds, we can always replace one $$$x$$$-cost operation with two $$$y$$$-cost operations.
$$$[2]$$$ If $$$d = 2$$$ and two $$$1$$$-s are not adjacent, the answer is $$$y$$$.
$$$[3]$$$ If $$$d \ne 2$$$, select $$$i$$$-th $$$1$$$ and $$$(i + \frac{d}{2})$$$-th $$$1$$$ each ($$$1 \le i \le \frac{d}{2}$$$). This costs $$$\frac{d}{2} \times y$$$, and we showed the cost cannot be reduced more in hint 3.
1733D2 - Zero-One (Hard Version)
Greedy solution used in D1 doesn't work in this version.
The restriction accepts normal $$$O(n^2)$$$ solution.
(Continued from D1 editorial)
If $$$x < y$$$, greedy approach used in D1 doesn't work. Let's use DP. Define $$$z0[i][j]$$$ as the minimal cost when there is $$$j$$$ $$$1$$$s in first $$$i$$$ elements of $$$c$$$ and $$$c_i = 0$$$, and $$$z1[i][j]$$$ as the minimal cost when there is $$$j$$$ $$$1$$$s in first $$$i$$$ elements of $$$c$$$ and $$$c_i = 1$$$. Initially all table values are $$$\infty$$$.
First, check $$$c_1$$$. If $$$c_1 = 0$$$, set $$$z0[1][0]$$$ to $$$0$$$. Otherwise, set $$$z1[1][1]$$$ to $$$0$$$.
Then, check the following elements from $$$c_2$$$ to $$$c_n$$$ in turn.
$$$[4]$$$ If $$$c_i = 0$$$,
$$$[5]$$$ If $$$c_i = 1$$$,
for $$$0 \le j \le i$$$. The answer is $$$z[n][0]$$$.
Solve $$$n \le 10^5$$$ version. Some testers found $$$O(n)$$$ solution.
1733E - Conveyor
Each second, slime ball moves to next diagonal.
Every slime always locates in different diagonal.
No two slime ball will merge forever.
If $$$t < x + y$$$, the answer should be "NO".
In the conveyor, cells with same $$$(i + j)$$$ value consists a diagonal ($$$i$$$ is row number, $$$j$$$ is column number). Let's call them $$$(i + j)$$$-th diagonal. So there are $$$239$$$ diagonals, from $$$0$$$-th to $$$238$$$-th.
So, we can find every slime ball move to the next diagonal for every second. It means no two slime ball merge forever.
Given $$$t$$$, $$$x$$$, $$$y$$$, cell $$$(x, y)$$$ belongs to $$$(x + y)$$$-th diagonal. If $$$t < x + y$$$, the answer is NO because there is no slime ball in $$$(x + y)$$$-th diagonal yet. If $$$t \ge x + y$$$, $$$(x + y)$$$-th diagonal contains one slime ball, and the ball is placed on cell $$$(0, 0)$$$ after $$$(t - x - y)$$$ seconds from the start. So $$$(t - x - y)$$$ slime balls passed this diagonal before.
Now, find out which cell contains slime ball among the diagonal. To do this, we use following method: simulate with $$$(t - x - y)$$$ slime balls to check how many slime reach each cell of the diagonal, and repeat this with $$$(t - x - y + 1)$$$ slime balls. Exactly one cell will show different result, and this cell is where $$$(t - x - y + 1)$$$-th slime ball passes through. If this cell is equal to $$$(x, y)$$$, the answer is YES. Otherwise the answer is NO.
Simulation with $$$x$$$ slime balls processes as follows:
- Place $$$x$$$ slime balls on cell $$$(0, 0)$$$.
- Move slime balls to next diagonal. For each cell, if the cell contains $$$k$$$ slime balls, $$$\lceil \frac{k}{2} \rceil$$$ moves to right and $$$\lfloor \frac{k}{2} \rfloor$$$ moves to down.
- Repeat the second step. If slime balls reached aimed diagonal, stop and find the result.
Increase the conveyor size to $$$10^4 \times 10^4$$$. Solve this version. Query number is same.











Can someone explain/share the O(N) solution of task D2?
If $$$x \geq y$$$, follow D1. Otherwise, for $$$x < y$$$, observe that for each mismatch, we can fix it by either performing a single $$$y$$$ operation with another non-adjacent mismatch, or we can perform a sequence of $$$x$$$-operations to either the next or previous mismatch. We can use a 1D DP as follows:
$$$dp[i]$$$ represents the minimum cost for dealing with the first $$$i$$$ mismatches alone. If $$$i$$$ is even, then all mismatches should be fixed. If $$$i$$$ is odd, then $$$i - 1$$$ mismatches should be fixed while one mismatch remains. The $$$mis[]$$$ array stores mismatch indices.
For even $$$i$$$, $$$dp[i] = \min (dp[i - 2] + (mis[i] - mis[i - 1])x, dp[i - 1] + y)$$$. We can fix the $$$i$$$-th mismatch through either an $$$x$$$-operation chain with the $$$(i - 1)$$$-th mismatch (first option), or through a $$$y$$$-operation with some earlier mismatch (second option).
For odd $$$i$$$, $$$dp[i] = \min (dp[i - 2] + (mis[i] - mis[i - 1])x, dp[i - 1])$$$. Here, for the $$$i$$$-th mismatch, the first option is the same as before ($$$x$$$-operation chain with $$$(i - 1)$$$-th mismatch), but the second option is to let the $$$i$$$-th mismatch be the unresolved one. Note that $$$dp[i - 1] \leq dp[i - 2] + y$$$ (see even formula), so there is no need to consider using a $$$y$$$-operation for the $$$i$$$-th mismatch for odd $$$i$$$ (but it wouldn't change the result if this was added as a candidate).
The last element in the $$$dp$$$ array (which must be an even index) is the answer.
This solution looks more elegant!
Very well explained, I understood it without trouble. This post should be in the editorial.
Better than the editorial. Thanks!
How would you add the the y-operation for odd i, if we wanted to? Also please can you explain a little why there is no need to consider the y-operation in case of odd i?
If you wanted to consider the $$$y$$$-operation for the last element of odd $$$i$$$, it would have a cost of $$$dp[i - 2] + y$$$ (so the second-to-last element is the unresolved one). However, we know that $$$dp[i - 1] \leq dp[i - 2] + y$$$ (because applying the even formula on $$$i - 1$$$ yields $$$dp[i - 1] = \min (dp[i - 3] + (mis[i - 1] - mis[i - 2])x, dp[i - 2], dp[i - 2] + y) \leq dp[i - 2] + y$$$). Therefore, for odd $$$i$$$:
$$$dp[i] = \min (dp[i - 2] + (mis[i] - mis[i - 1])x, dp[i - 1], dp[i - 2] + y) = \min (dp[i - 2] + (mis[i] - mis[i - 1])x, dp[i - 1])$$$
Thanks for replying! But I still have one doubt... for y-operation for last element of odd i, why have you only tried — by keeping either last element unresolved or second last element unresolved? Why didn't you try keeping any other element unresolved?
All other options are implicitly covered by $$$dp[i - 2]$$$, which denotes the optimal way of handling the first $$$i - 2$$$ elements. I should correct my earlier statement actually: $$$dp[i - 2] + y$$$ does not only cover the case where the second-to-last element is unresolved, but it actually covers the cases where any of the first $$$i - 1$$$ elements are unresolved.
However, note that the different options is not about "which element is unresolved" but more about "how do we deal with the last element". We can break this down to four options:
Don't pair the last element: this costs $$$dp[i - 1]$$$. It would, of course, also be the unresolved element in this case.
Pair it with the second-to-last element using an $$$x$$$-operation chain: this costs $$$dp[i - 2] + (mis[i] - mis[i - 1])x$$$. Here, the unresolved element is whoever was unresolved in $$$dp[i - 2]$$$ (which is the optimal choice among the first $$$i - 2$$$ elements).
Pair it with the $$$(i - 1)$$$-th element using a $$$y$$$-operation (assuming they're not adjacent). The cost here is $$$dp[i - 2] + y$$$. Again, the unresolved element is whoever was unresolved in $$$dp[i - 2]$$$. The assumption of non-adjacency is not an issue, because if the last two elements were adjacent, then option 2 would win over option 3 (since $$$x < y$$$).
Pair it with one of the first $$$(i - 2)$$$ elements using a $$$y$$$-operation. The optimal way to deal with the first $$$(i - 2)$$$ elements is given with $$$dp[i - 2]$$$, which includes one unresolved element among them. Therefore, the optimal way to handle this case would be to pair the last element with whoever is unresolved from $$$dp[i - 2]$$$. This does mean that the $$$(i - 1)$$$-th element is not handled, so it would end up becoming the unresolved one. The cost here is also $$$dp[i - 2] + y$$$.
If the fourth option still confuses you, let me elaborate a little more: we are not specifically choosing that the $$$(i - 1)$$$-th element is the unresolved one, but rather, we are choosing to let the last element pair with some element from among the first $$$(i - 2)$$$ elements. The optimal choice here is to pair it with the unresolved element in $$$dp[i - 2]$$$. [Proof: if it's better to pair it with some different element $$$j$$$, this would imply that leaving $$$j$$$ unresolved would be better for the value of $$$dp[i - 2]$$$ than whichever element was actually left unresolved]. And this would naturally lead to the $$$(i - 1)$$$-th element being the unresolved one, since all other elements are handled.
In reality, there is no actual difference between options 3 and 4. They can both be combined into a single case of "use a $$$y$$$-operation on the last element". With an understanding of how a $$$y$$$-operation works, where the cost is the same irrespective of which element we pick (as long as it's non-adjacent, but option 2's superiority would dominate such scenarios), it should be intuitive to observe that it doesn't actually matter as to which element we are pairing it, a long as it's a $$$y$$$-operation.
Finally, given that the unresolved element would eventually have to be resolved in later even cases, either through an $$$x$$$-operation chain with the next element (which requires that the last element is the unresolved element) or a $$$y$$$-operation with some element (where there is no advantage for any particular element over another), it's easy to see that keeping the last element unresolved cannot be worse than to pair it up with a $$$y$$$-operation so that someone else can wait for a future $$$y$$$-operation, i.e., option 1 will never be worse than options 3 or 4.
Sorry for the wall of text; I think this scenario is actually really simple intuitively, but I can understand that one might have doubts about whether this intuition is rigorously proven, so I hope I was able to ease some of those doubts.
NB
i have a little doubt in this solution, can you please explain? you defined your dp state as : dp(i) = minimum cost for dealing with the first i mismatches "ALONE". now let's take the even case only : suppose you do a y-operation on the i-th mismatch with some previous mismatch j, now after this transition, can the new state really be defined by dp(i-1) as per the rules because when we were at the ith state(precisely speaking when we started the state at dp(i), all the previous mismatches before ith one were not fixed yet, but when we perform a y-operation, with some jth mismatch, it has already been fixed, so its not correct to say this state is dp(i-1), furthermore say for example that we fixed the ith mismatch using a y operation with the (i-2)th mismatch, now when we use dp(i-1), there is an operation in the transition equation that is done with the just previous mismatch using an x operation: (mis[i]-mis[i-1])x but when we are dp(i-1) now, this would be (mis[i-1]-mis[i-2])x but why would we perform this x operation when the (i-2)nd mismatch has already been resolved)
I'm not entirely sure I understand your question. Let's say $$$i$$$ is even and we decide to resolve the $$$i$$$-th mismatch using a $$$y$$$-operation. There are $$$i - 1$$$ earlier mismatches that we could pair with the $$$i$$$-th mismatch. Let's assume that the optimal solution arises when we pair the $$$i$$$-th mismatch with the $$$j$$$-th mismatch ($$$j < i$$$).
Claim: The value of $$$dp[i - 1]$$$ is equal to the cost of dealing with the first $$$i - 1$$$ mismatches except for the $$$j$$$-th mismatch.
Proof: By definition, $$$dp[i - 1]$$$ is the optimal way to deal with the first $$$i - 1$$$ mismatches except with one left unresolved. Suppose this unresolved mismatch is the $$$k$$$-th mismatch. Consider three cases:
Case 1: The minimum cost when the $$$k$$$-th mismatch is unresolved is equivalent to the minimum cost when the $$$j$$$-mistamtch is unresolved. The claim holds in this case. This also includes the case of $$$k = j$$$ btw.
Case 2: The minimum cost when the $$$k$$$-th mismatch is unresolved is higher than the minimum cost when the $$$j$$$-mistamtch is unresolved. Then $$$dp[i - 1]$$$ is not the optimal way of dealing with the first $$$i - 1$$$ indices, which is a contradiction.
Case 3: The minimum cost when the $$$k$$$-th mismatch is unresolved is lower than the minimum cost when the $$$j$$$-mistamtch is unresolved. This means that when we need to deal with the $$$i$$$-th mismatch, it would be better to pair the $$$i$$$-th mismatch with the $$$k$$$-th mismatch as opposed to the $$$j$$$-mismatch. This contradicts the premise that the optimal way to deal with the $$$i$$$-th mismatch is to pair it with the $$$j$$$-th mismatch.
Therefore, only Case 1 is valid, proving the claim. This also means that $$$dp[i] = dp[i - 1] + y$$$, since $$$dp[i - 1]$$$ gives us the cost of dealing with the first $$$i - 1$$$ mismatches except for the $$$j$$$-th mismatch, which we pair with the $$$i$$$-th mismatch for a cost of $$$y$$$.
Does this resolve your confusion, or did I misunderstand your query?
this was my exact query, thanks for the explanation, its really very well explained.
There is a solution with an $$$O(n)$$$ DP.
For $$$x\ge y$$$ the solution is obvious (it's Problem D1), so I'll assume that $$$x<y$$$ then.
First, pre-process $$$dif[i]$$$ which means the index of $$$i$$$-th difference between a and b.
Let $$$f[i]$$$ be the minimum cost to make first $$$i$$$ differences became same. It's impossible when $$$i$$$ isn't even, so if $$$i$$$ is odd, $$$f[i]$$$ becames the minimun cost to make that there's only one difference in the first $$$i$$$ differences.
Before we begin to solve, let $$$f[0]$$$ and $$$f[1]$$$ be $$$1$$$ first.
Then, we can calculate $$$f[i]$$$ for all $$$i$$$ from $$$2$$$ to $$$n$$$ in order:
If $$$i$$$ is even, $$$f[i]$$$ can be $$$f[i-2]+min(x\times(dif[i]-dif[i-1]),y)$$$. $$$f[i-2]$$$ means the cost when $$$dif[1\to i-2]$$$ are all solved, and $$$f[i]$$$ means the cost when $$$dif[1-i]$$$ are solved, so $$$f[i]$$$ need to add the cost to make $$$dif[i]$$$ and $$$dif[i-1]$$$ same.
$$$f[i]$$$ can also be $$$f[i-1]+y$$$. $$$f[i-1]$$$ means the cost when there's only one difference in $$$dif[1\to i-1]$$$, and $$$f[i]$$$ means there's no difference, so it has to add the cost to make $$$dif[i]$$$ and $$$dif[j]$$$ same. Although we don't know the real $$$j$$$, we know the cost is $$$y$$$, because the condition that $$$j=i-1$$$ has already solve by the last paragraph, so we can assume that $$$j<i-1$$$.
To sum up, the real $$$f[i]$$$ need to be the minimum cost between last two condition.
When $$$i$$$ is odd, the reasoning process is similar. $$$f[i]$$$ can be $$$f[i-2]+min(x\times(dif[i]-dif[i-1]),y)$$$, or $$$f[i-1]$$$. You can try to independently calculate.
Here is my code, you can refer to it.
Thanks for the explanation.
I have seen another tricky solution: We will exclude the x>=y as we can solve it with D1 solution and the case where only 2 nearby mismatches( ans=min(2*y,x) ),
(Option#1): So you will try to jump to any other mismatch with cost Y and goes to the next mismatch (dp[i] = dp[i+1] + y), I think this is valid because if you will take any mismatch with cost Y you will pair it with another mismatch.
The problem with option 1 is calculating Y for every mismatch, so you have to count the number of mismatches taken by the first option and divide them by 2 , to avoid that, you can just multiply the second option (x) by 2 and divide the final solution by 2.
(Option#2): The other transition is to chain with the next one(i+1) and transition to (i+2) so you solved i and i+1 mismatches with cost x*(mismatch[i+1] — mismatch[i+2]). option 2 is only valid if there exists (i+1<n). dp[i] = min(dp[i],dp[i+2] + x*(mismatch[i+1] — mismatch[i+2]))
solution credits to IsaacMoris
let v be the sorted vector of indices where a[i]!=b[i] (let size of v be vn) then the answer of the problem is f(0)
where, cost(i,j)=min(y,|v[i]-v[j]|*x)
f(vn-1)=y,f(cn-2)=cost(vn-1,vn-2)
f(i) = min(((vn-i)%2)*y + f(i+1),cost(i,i+1)+f(i+2))
was this blog in 'draft' for 2 years?
Yes.
Hello Guys! For D2 I had this solution 172748609, I also don't no the reason that why its true.Can any one hack or say the reason behind it?
First, we get all the positions which satisfy a!=b and save them in a new array C. Then we consider four positions which are adjacent in C. Let them be p1,p2,p3,p4 (p1<p2<p3<p4) . There is always min((p2-p1)*x,y)+min((p4-p3)*x,y)<=min((p3-p1)*x,y)+min((p4-p2)*x,y), which means that (p1,p3)+(p2,p4) can't be a part of answer. So you are right :)
Why do you say that a greedy solution does not work in D2. I think it's too bad that such tasks appear in the competition!
Edited the phrase more clearly.
LoL, what did u expect from the fifth problem?
I'm pretty sure the post was to be interpreted with a "/s", considering the "not so unusual" hint (as it was before 351F44 edited it).
Hello guys, would really appreciate a little help with the B question. I thought that if we can make a combination with the 2 values of x and y that sums up to length-1 then we will get the right answer(was not sure so just tried). So I ran binary search between 0 and length-1 to search for the number of players that had x wins to find the answer and then print the player x times, but I got WA. here is the code:https://codeforces.net/contest/1733/submission/172718129 kindly guide me, thank you. EDIT:I found the error,it was a silly mistake in the printing part.THe code is working fine now. Code:https://codeforces.net/contest/1733/submission/172869494
Binary search only works on monotonic searching space. Simple words, if x works either y > x or y < x should work. I am not sure how this problem is related to binary search. Maybe explain why you think binary search will do here.
Does anyone have a solution for D2 using DP with memoization?
You can check my solution: 172731715,
DP[l][r] = min(DP[l][r], dp(l, r — 2) + dp(r — 1, r));
can you please explain why this condition is necessary to check if have done
DP[l][r] = min(DP[l][r], dp(l, l + 1) + dp(l + 2, r));
So my intuition is:
r^th element will either go with l^th element =>DP[l][r] = min(DP[l][r], dp(l + 1, r — 1) + y); or, r^th element will go with greater (l+1) th element.
Let us say we have a vector of mismatched indices. We will be picking from this vector in pairs.
In the DP, at any mismatched index, we have following options:
Here is my submission https://codeforces.net/contest/1733/submission/172860412
In D2(editorial), how is it possible to have $$$i+1$$$ ones in the first $$$i$$$ elements of $$$c$$$?
i is correct. Now edited. Thanks for noticing me.
I think there is one more problem with it.
You recalculate dp for all $$$0 \le j \le i$$$, but in formulas where $$$c_i=1$$$ there is a condition $$$j=i+1$$$.
Edited, thanks. There was some mistake while translating 0-based MCS into 1-based editorial.
What would be the expected rating of the first 2 questions?
We estimated A as *800, B as *1000 or *1100. Let's wait.
and C?
I think *1500.
Are you sure? I normally can't solve 1500s but C and even D1 were pretty solvable for me
Same, I was guessing around 1300.
Well, standing says it can be easier than *1500. It is what I estimated before the contest, maybe real difficulty is more easier? :/
Yeah could be. Thank you for the contest tho! Great problems.
Great Problem E! Though its implementation isn't complicated, its idea is quite thought-provoking and requires insight. This is how CF problems must be. Truly nice problem!
Is the challenge for E solvable?
I don't know.
I think it's plausible. Consider the state of the conveyer after using exactly k slimes and look at each diagonal, regarding right arrow as 0 and down arrow as 1. For example, when k = 0, all conveyers have right arrows, so all diagonal's values are 0. When k = 1, all conveyers except the first row have right arrows, so all diagonal's values are 1.
As k increases,
1st diagonal's values are: 0, 1, 0, 1, ....
2nd diagonal's values are: 00, 01, 11, 10, 00, ...
3rd diagonal's values are: 000, 001, 011, 001, 101, 100, 110, 100, 000, ...
4th diagonal's values are: 0000, 0001, 0011, 0111, 0011, 0001, 0011, 0111, 1111, 1110, 1100, 1000, 1100, 1110, 1100, 1000, 0000, ...
It's not something I really proved, but it seems there's an obvious pattern here. I guess this pattern will allow us to find a path for k-th slime in O(N log k) for a N*N conveyer system.
I'm curious to know how to solve problem c challenge, any hints ?
Please, share solution for Problem C challenge. Thanks.
You can always make the whole array equal to the last element of the array in n-1 steps.
First, apply the operation on the first and the last element. After this the first and the last element will become equal.
Now just iterate through the array starting from the second element:
Case 1. If the current element has the same parity as the last element apply operation to the current and the last element. This will make the current element equal to the last.
Case 2. Otherwise, apply the operation to the current and the previous element. This will make the current element equal to the previous. But we know that the previous element is already equal to the last because we already iterated through it, so this will make the current element equal to the last.
Have you solved the "Challenge" given , finding minimum operations ?
Did you get it ?
Difference between E's solution I submitted in last two minutes and the AC solution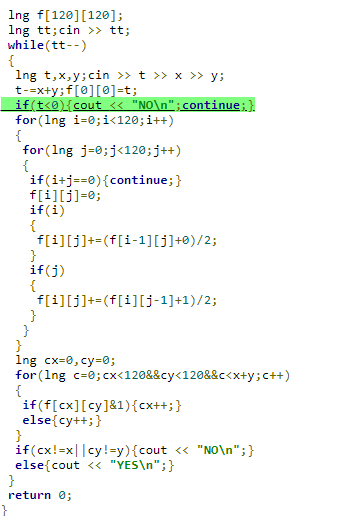
Hello, constructive can you please tell in the question D1 & D2, how you even have a intuition of starting with the XORs of both the binary strings a and b. At my last thought after so long I could only think of working on b trying making equalto a. But actually of no use because it's the same thing.
So how you even got the intuition of working on XORs of both the strings??
It is one of the result of an observation. To do such observation, check if it can be transformed to be structurally identical.
There was an incorrect solution get accepted on D2 during the contest, and unfortunatly didn't get hacked. The idea was use range(or interval?) DP with some strange strategies to enumerate the decision. Code link
Hope to strengthen the data soon.
Now, find out which cell contains clime ball among the diagonal.
Edited. Thanks!
For the problem E, is it possible to find out the periodicity of a particular roller in $$$O(1)$$$ time or precompute them after which we can simulate the process for the slime that arrived at $$$t-x-y$$$ in $$$O(x+y)$$$ ?
I don't have a concrete idea yet on how would one calculate the periodicity tho :( Any suggestions would be helpful! I feel one could exploit this to solve the challenge as well?
So I tried to print the pattern of the state of each roller form t = 1 till t = 50 and 0 represents right and 1 represents down and in the beginning between
{1,0}and{0,1}you see a good pattern. but in the diagonal(x+y = 2)There doesn't seem to be a pattern that is being followed, but there seems to be some similarity in{0,2}and{2,0}perhaps but{1,1}seems to show no similarity ? And when we try talking about the diagonal(x+y = 3)I can't spot any good pattern. So I'm skeptical of being able to find a pattern in the periodicity although I'm almost certain that the states of all rollers are periodic in nature.At E, I could think everything in time but the most important part, the simulation with x slime balls processes. How can I approach that process from the hints?
I wonder for D2, if we can just use DP to solve all the conditons? So if x>y, can we use DP instead of greedy algorithm? I try it, but got wrong answer.
Shout out for problem E. You broke CF's top rated member, and it took me a full day to solve it, well done
Can somebody hack my solution? https://codeforces.net/contest/1733/submission/179012720 I think it might be wrong.
can anyone elaborate the proposed solution of D2 in deep details, about the transitions given(how did we get those transitions). Actually i am unable to make out much from the proposed solution
For D1 consider this test case:
a and b are different in [1,6,7,10] indices ** according to editorial's solution, [1,7] with cost 8 and [6,10] with cost 8 so ans = 8+8 = 16. but the min cost is to take [6,7] with cost 2 and [1,10] with cost 8 so ans = 2+8 = 10.
Do I miss something?
Sorry I just realized that x>=y :(
why was n less 3000 in D1 given the editorial provides a O(N) solution?
/* in this question we have to make two strings equal by performing some operations and we have some cost associated with the two operations x when r-l = 1 y when r-l != 1 we can basically change two numbers simultaneously either zero to one or one to zero significance of it is that we choose two numbers so numbers are basically form a pair */
/* when x >= y (easy version) we can find the indices where we have different bits in the two strings and if the count is odd then we cannot make pairs such that all elements are paired and no one is left unpaired so the answer is -1
when we have the indices of bad elements ( not equal bits positions ) so if there are only two postions so we have to check if the two elements are consecutive or not if consecutive then find minimum of min(x,2*y) because we directly change two by using x or we can change one by one by pairing with some far element
and if there are more elements the answer will be count/2 * y because in this case we can always pair the elements without being making them consecutive elements in the pair */
/* when there is no boundation on x ( hard version ) we have discussed the case when x >= y now we will discuss for x < y here greedy will not work so we have to use dp here instead but question is how
now we have bad elements (indices of not equal bits )
lets take an example x = 2 and y = 11 and s1 = 000001 and s2 = 100000
indices of bad elements -> 1 and 6
so what we can do now either pick 1 and 6 and take a cost of y which is 11 or we change basically flow the change like , making changes in s1 s1 becomes 000010 then 000100 then 001000 then 010000 then 100000 now both s1 and s2 are equal so total cost is distance between two bits (distance that flow of change has covered) * x that is x*(6-1) 2*5 = 10 so optimal will be to use flow technique for minimum cost so answer will be 10
so now let's think we have two indices so we can either use dis * x or y which is minimum so will use dp here
we will use dp on bad elements (indices of not equal bits) so we will have an array of bad elements
now we will generate the minimum answer for all subarrays of the array of bad elements
let's take an example: array is -> 1 4 5 6 7 10 and x = 1 and y = 3 so answer for 2 size subarrays will be 3 1 1 1 3 now we will generate answer for all 4 size subarrays we will generate all even size subarrays as we will add a pair of elements in our calculated subarray
so answers will be 1 4 5 6 -> 4 , 4 5 6 7 -> 2 , 5 6 7 10 -> 4 no the answer for full array means 6 elements 1 4 5 6 7 10 6 -> 6
now what can be the transitions : lets say you are forming the 6 length subarray 1 4 5 6 7 10 (previous example ) you can generate it from 4 length and 2 length subarrays ( previously calculated )
so there are three possibilities 1: 1 4 + 5 6 7 10 2: 1 4 5 6 + 7 10 3: 1 + 4 5 6 7 + 10 in the first and second case we can add the answer of two subarrays let it be ans1 = 1 4 + 5 6 7 10 -> 3 + 4 = 7 ans2 = 1 4 5 6 + 7 10 -> 4 + 3 = 7 and for the last case the answer will be answer of subarray + min(dis*x,y) so ans3 = 1 + 4 5 6 7 + 10 -> 2 + min((10-1)*1,4) => 2 + 4 = 6 that is the answer and store the answer as minimum of all the three answers i.e. min({ans1,ans2,ans3}) in dp
in this way the answer for the whole array is calculated now you will say that r-l = 1 condition is not mentioned it is not needed indeed in this case as is distance is 1 and x is smaller then x*1 will be smaller than y so it is chosen automatically and answer will be in dp[1][array.size()-1]
the base condition will be to calculate the answer for all 2 size subarrays */
/* hope you get the solution if have any doubt you can message me i am free to help
<--------------------------------- THANK YOU ------------------------------------> */
https://codeforces.net/contest/1733/submission/204996759
Thanks for the Explanation !
Did anyone solve the challenge in problem c ?
in D1 problem, One x cost operation can be replaced with two y cost operations. can anyone explain me how this has happenend?