Recently I attended YANDEX qualification round and i solved 2 problems. When the solution came out, i realized that there is no tutorial, so i didn't manage to understand problem C by just viewing the source. Can you explain this task particularly and probebly some other too? A LOT OF THANKS!!!
UPD. What about the rest of the tasks. Can you give any hints?











you have to count the number of winning moves in the game of Nim, it is well known problem http://en.wikipedia.org/wiki/Nim
Unfortunately, the heaps are 2*10^9 so a straight algo wont work :(
You can calculate nim-sum bit by bit. Suppose, n = 5:
Now consider the nim. Obviously, the bit in nim is 1 iff the number of corresponding 1-bits in all piles is odd. So, all you have to do is to count the number of 1-bits in all the piles for the given nim bit. An easy task to do once you notice that bit pattern is periodic (01 for 0th bit, 0011 for the 1st, 00001111 for the 2nd, etc.)
Good, but how can you compare whether the nim is smaller than the heap fast.
What you actually need to do is:
1. Find the nim-sum of all the numbers from 1 to N (using the approach described)
2. Find the most significant bit of that nim-sum
3. Find the number of piles with this bit set to 1. (Using the very same approach. You can even use the results from the first step.)
UPD. It's just occurred to me. Why even bother and find actual nim-sum? Combine 3 steps into one: just find the highest bit for which the number of piles with this bit set is odd. That odd number is your answer (0 if there's no such bit). I've just accepted this idea.
UPD. It's just occurred to me. Why even bother and find actual nim-sum? Combine 3 steps into one: just find the highest bit for which the number of piles with this bit set is odd. That odd number is your answer (0 if there's no such bit). I've just accepted this idea.
Can you give an example? I still dont understand it. :(
it is easy to google direct formula for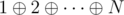 :
:
s(N) = N & (N % 2 ? 0 : ~0) | ( ((N & 2)>>1) ^ (N & 1) )Hey, give me this link right now and take my money!!!)
http://stackoverflow.com/questions/3932346/direct-formula-for-summing-xor
Or just: