Author: AlexSkidanov
What happens if the rectangles form an N × N square? Then these two conditions are necessary.
1) The area must be exactly N × N.
2) The length of its sides must be N. That means, the difference between the right side of the rightmost rectangle — the left side of the leftmost rectangle is N. Same for topmost and bottommost rectangles.
We claim that, since the rectangles do not intersect, those two conditions are also sufficient.
This is since if there are only N × N space inside the box bounded by the leftmost, rightmost, topmost, and bottommost rectangles.
Thus if the sum of the area is exactly N × N, all space must be filled -- which forms a square.
Author: nika
Suppose the "divide-by-two" stage happens exactly D times, and the round robin happens with M people.
Then, the number of games held is: 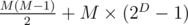
We would like that 
This is an equation with two variables -- to solve it, we can enumerate the value of one of the variables and calculate the value of the other one. We cannot enumerate the possible values of M, since M can vary from 1 to 10^9. However, we can enumerate D, since the number scales exponentially with D -- that is, we should only enumerate 0 ≤ D ≤ 62.
Thus, the equation is reduced to 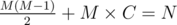
Since this function is increasing, this can be solved via binary search on M.
Author: AlexSkidanov
First part of the problem is to find minimum number of diamonds one can achieve by starting with a given monster. To do so, we will be using Dijkstra algorithm. Originally we don't know the minimum for any monster. For every rule we will maintain how many monsters with unknown minimums it has (let's call it ki for the i-th rule). Let's take every rule that has only diamonds in it (i.e. which has ki = 0), and assign number of diamonds in that rule as a tentative minimum for the monster (if a monster has several diamonds-only rules, take the smallest one). Then take the monster, that has the smallest tentative minimum currently assigned. For that monster the tentative value is the actual minimum due to the same reasoning we use when we prove correctness of Dijkstra algorithm. Now, since we know the minimum for that monster, for every rule i that has that monster in its result subtract 1 from ki for every occurrence of the monster in the result of that rule. If for any rule the value of ki becomes zero, update the tentative minimum for the monster that rule belongs to with the sum of minimum values for each monster that rule generates plus the number of diamonds that rule generates. Then from all the monsters for which we don't known the minimum yet, but for which we know the tentative minimum, pick the one with the smallest tentative minimum, and continue on.
At the end we will end up in a state, when each monster either has an actual minimum value assigned, or has no tentative value assigned. The latter monsters will have - 1 - 1 as their answer. For the former monsters we know the minimum, but don't know the maximum yet.
The second part of the problem is to find all the rules, after applying which we are guaranteed to never get rid of all the monsters. We will call such a rule bad. It is easy to show, that the rule bad if and only if it generates at least one monster with minimum value of -1. Remove all the bad rules from the set of rules.
When bad rules are removed, finding maximums is trivial. Starting from every node for which maximum is not assigned yet, we traverse all the monsters in a DFS order. For a given monster, we consider every rule. For a given rule, for each monster it generates, we call DFS to find its maximum value, and then sum them up, add number of diamonds for the rule, and check if this rule gives bigger max value than the one currently known for the monster. If we ever call DFS for a monster, for which we already have a DFS call on the stack, that means that that monster has some way of producing itself (directly or indirectly) and some non-zero number of diamonds (this is why problem statement has a constraint that every rule generates at least one diamond), so the answer for the monster is -2. If, processing any rule, we encounter a monster with max value -2, we immediately assign -2 as a max value for the monster the rule belongs to and return from the DFS.
As an exercise, think of a solution for the same problem, if rules are not guarantee to have at least one diamond in them.
Author: dolphinigle
Assume there's an extra sea cells on a row above the topmost row, and a row below the bottom most row. Hence, we can assume that the top and bottom row consists entirely of sea.
We claim that: There does not exist a sea route if and only if there exists a sequence of land cells that circumfere the planet (2 cells are adjacent if they share at least one point).
The "sufficient" part of the proof is easy -- since there exists such a sequence, it separates the sea into the northern and southern hemisphere and this forms a barrier disallowing passage between the two.
The "necessary" part. Suppose there does not exist such route. Then, if you perform a flood fill from any of the sea cell in the top row, you obtain a set of sea cells.
Trace the southern boundary of these set of cells, and you obtain the sequence of land circumfering the planet.
Thus, the algorithm works by simulating the reclamations one by one. Each time a land is going to be reclamated, we check if it would create a circumefering sequence. We will show that there's a way to do this check very quickly -- thus the algorithm should work within the time limit.
Stick two copies of the grid together side-by-side, forming a Rx(2*C) grid. The leftmost and rightmost cells of any row in this new grid are also adjacent, similar to the given grid.
Each time we're going to reclamate a land in row r and column c, we check if by doing so we would create a path going from (r, c) to (r, c + C). If it would, then we cancel the reclamation. Otherwise, we perform it, and add a land in cell (r, c) and (r, c+C).
This "is there a path from node X to node Y" queries can be answered very very quickly using union find -- we check whether is it possible to go from one of the 8 neighbors of (r, c) to one of the 8 neighbors of (r, c+C).
Correctness follows from the following: There exists a circumefering sequence IFF there exists a path from (r, c) to (r, c+C). Sufficient is easy. Suppose there exist a path from (r, c) to (r, c+C). We can form our circumfering sequence by overlapping the path from (r, c) to (r, c+C) with the same path, but going from (r, c+C) to (r, c) (we can do this since the grid is a two copies of the same grid sticked together).
Necessary. Suppose there exists a circumfering sequence. We claim that there must exist a path to go from (r, c) to (r, c+C). Consider the concatenation of an infinite number of our initial grid, forming an Rx(infinite * C) grid. If there exists a circumfering sequence, we claim that within this grid, there exists a path from (r, c) to (r, c+C).
Suppose there does not exist such a path. Since there exists a circumfering sequence, it must be possible to go from (r, c) to (r, c+ t * C), where t is an integer >= 2. Now, you should overlap all the paths taken to go from (r, c) to (r, c+t*C) in the grid (r', c' + C) (the grid immediately to the right of the grid where (r, c) is located). There must be a path from (r, c) to (r, c+C) in this new overlapped path.
Proofing the final part is difficult without interactive illustration -- basically since t >= 2, there exists a path that goes from the left side to the right side of the grid (r', c' + C). This path must intersect with one of the overlapping paths, and that path must be connected to (r, c+C). The details are left as... exercise :p.
Author: nika
In this part of editorial, all numbers we speak are in modulo N. So, if I say 10, it actually means 10 modulo N.
First, observe that this problem asks us to find a cycle that visits each node exactly once, i.e., a hamiltonian cycle. Thus, for each node X, there exists one other node that we used to go to node X, and one node that we visit after node X. We call them bef(X) and aft(X) (shorthand for before and after).
First we will show that if N is odd, then the answer is - 1.
Proof...? Consider node 0. What nodes points to node 0? Such node H must satisfy either of the following conditions:
2H = 0
2H + 1 = 0
The first condition is satisfied only by H = 0. The second condition is satisfied only by one value of H: floor(N / 2).
So, since we need a hamiltonian cycle, pre[0] must be floor(N/2), and aft[floor(N/2)] = 0
Now, consider node N - 1. What nodes points to node N - 1?
2H = N - 1
2H + 1 = N - 1
The second condition is satisfied only by H = N - 1. The first condition is satisfied only by H = floor(N / 2)
But we need a hamiltonian cycle, so aft[floor(N/2)] must be N - 1. This is a contradiction with that aft[floor(N/2)] must be 0.
Now, N is even. This case is much more interesting.
Consider a node X. It is connected to 2X and 2X + 1. Consider the node X + N / 2. It is connected to 2X + N and 2X + 1 + N, which reduces to 2X and 2X + 1.
So, apparently node X and node X + N / 2 are connected to the same set of values.
Now, notice that each node X will have exactly two nodes pointing to it. This is since such node H must satisfy
2H = X
2H + 1 = X
modulo N, each of those two equations have exactly one solution.
So, this combined with that node X and X + N / 2 have the same set of connected nodes means that the only way to go to node 2X or 2X + 1 is from nodes X and X + N / 2.
Thus, if you choose to go from node X to node 2X, you HAVE to go from node X + N / 2 to node 2X + 1 (or vice versa).
Now, try to follow the rule above and generate any such configuration. This configuration will consists of cycles, possibly more than 1. Can we join them into a single large cycle, visiting all nodes?
Yes we can, since those cycles are special.
Weird theorem: If there are 2 + cycles, then there must exist X and such node X and node X + N / 2 are in different cycles.
Proof: Suppose not. We show that there must exist one cycle in that case. Since node X and X + N / 2 are in the same cycle, they must also be in the same cycle as node 2X and 2X + 1. In particular, node X and 2X and 2X + 1 are all in the same cycle. It is possible to go from any node X to any node Y by following this pattern (left as exercise). Now, consider the X such that node X and node X + N / 2 are in different cycles. Suppose we go from node X to node 2X + A, and from X + N / 2 to 2X + B (such that A + B = 1). Switch the route -- we go from node X to 2X + B and X + N / 2 to 2X + A instead. This will merge the two cycles -- very similar to how we merge two cycles when finding an eulerian path. Thus, we can keep doing this to obtain our cycle!
...It's not entirely obvious to do that in O(N) time. An example solution: use DFS. DFS from node 0. For each node X:
if it has been visited, return
if X + N / 2 has been visited, go to either 2X or 2X + 1 and recurse, depending on which route used by node X + N / 2
otherwise, we go to node 2X and recurse. Then, check if X + N / 2 was visited in the recursion. If it was not, then the two of them forms two different cycles. We merge them by switching our route to 2X + 1 instead, and recurse again.











About program E:
Actually, as far as I understand, that's exactly the search for Eulerian cycle in a graph on N/2 vertices. Let's put numbers 2i and 2i + 1 in one class, and draw an edge from i-th class to j-th class if there is an edge between their vertices in original graph. Then the edges go from class i to classes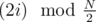 and
and 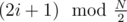 — just like in the original graph but with N replaced by
— just like in the original graph but with N replaced by 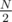 ! Now if we're in a vertex 2i of original graph, then we can leave it only by one edge in the new graph, because vertices 4i and 4i + 1 belong to the same class. So if we visited both vertices 2i and 2i + 1 in original graph, it means that we visited the vertex i in the new graph twice, and exited it by 2 different edges. That proves that the corresponding path in the new graph is Eulerian cycle and gives an algorithm to recover the original cycle from this Eulerian one.
! Now if we're in a vertex 2i of original graph, then we can leave it only by one edge in the new graph, because vertices 4i and 4i + 1 belong to the same class. So if we visited both vertices 2i and 2i + 1 in original graph, it means that we visited the vertex i in the new graph twice, and exited it by 2 different edges. That proves that the corresponding path in the new graph is Eulerian cycle and gives an algorithm to recover the original cycle from this Eulerian one.
The problem C has interesting interpretation. We have a context-free grammar (robots are nonterminals and diamonds are terminals). And the questions of the problem are to find lengths of the shortest/longest strings that can be produced from each nonterminal.
Is that origin problem formulation?
P.S. Code in grammar terms: http://codeforces.net/contest/325/submission/4067816
Yes, it is the origin of the problem. I was using it to optimize a CFG parser in one of my projects, so that it doesn't even try to parse a string, if its length is outside of [min, max] boundaries.
In B, I solved (M*(M-1))/2 + M*C = N, as a quadratic equation in M, rather than using binary search on M, but i got WA. I did not use BigInt. Is it due to overflow issues?
I did the same, but using BigIntegers and only integer numbers. Also got WA on pretest 5
I was also getting WA on 5, but that was an implementation error. Now getting WA on 38.
True, I also had implementation error, now AC — http://codeforces.net/contest/325/submission/4068404
Thanks, that means my WA is due to overflow only.
each of those two equations have exactly one solution.Actually one of them has no solutions and the other one has two.
Since
Nis even then parity ofXmakes sense moduloN.So if, e.g.,
Xis even, then2 H + 1 = X (mod N)has no solutions,while
2 H = X (mod N)has two —X/2and(X+N)/2.Thanks for problem D, it is really nice. The second part (when we note that the cut is an 8-neigours grid cycle) can be also solved like 196B - Бесконечный лабиринт.