kostka's blog

Google Kick Start 2020 — round G
By kostka, 4 years ago, In English

Round G of Google Kick Start 2020 will start this Sunday (October 18) at 12:00 UTC and will last 3 hours.

See you at g.co/kickstart.

  • Vote: I like it
  • +70
  • Vote: I do not like it

Comments Comments (57)
| Write comment?
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone else facing long queues?

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve C

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it
    1. sort the array and append the whole array with value a[i] + n.
    2. For each window w, find the moves required to make all values equal to median which is basically Sliding Cost on CSES. You can see discussion here

    Code

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you share your submission?

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You can view my submissions here.

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Can you explain the idea behind these lines of code in your solution?

          d=d+abs(m-a[i])-abs(old_m-a[i-k]);
if(k%2==0) d-=(m-old_m);
          → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    Ternary search on the target node worked for me.

    → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I used binary search in the following manner
    Let the array be 1 2 3 4 5 6 7 8 9 10 11 12 13 14 then calculate prefix sums, for each i [1,14] we calculate two index, index1 = the point where each element before will be wrapped around using Subtraction, index2 = from where it would be wrapped around from addition
    eg i=9 index1=2, so all elements before this will be wrapped using Subtraction. And from 2-> 9 all element just add.
    similarly index2.
    index1 and 2 can be calculated using binary search, and then you can use prefix sums and array values to get the answer

    → Reply
»
4 years ago, # |
  Vote: I like it +1 Vote: I do not like it

My main interests are problem C (Combination Lock) and D (Merge Cards).

  1. Did anybody solve C without using ternary search on the final target? I am sure there is a solution avoiding ternary/binary searches.

  2. In problem D after some standard thinking it's fairly possible to come up with an n^2 approach. Is it possible to solve the problem faster maybe O(nlogn) or even O(n)?

P.S. Since the main goal of Kickstart round is to contribute to recruiting at Google, what do you think how much is the ranking threshold this time to be contacted by Google requiter? What do you think about that magic number?

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    Does ternary search work in problem C ? How is the function unimodal ? I kept on getting WA using ternary search.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I also didn't manage to prove the unimodality. That was just an assumption + some random heuristic that worked.

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can you please see why my ternary search solution gave WA ?

        Spoiler
        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          The ternary search solution isn't correct. I just managed to get accepted because the tests were not strong enough.

          Here is my solution link https://pastebin.pl/view/bfb7d20d with a random heuristic.

          → Reply
          • »
            »
            »
            »
            »
            »
            4 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            Don't know about your solution but i think ternary search in following way will work .

            1.Sort the array of weights (say "$$$w$$$"). 2.Traverse the array.For index $$$i$$$ , minimum cost for converting all other elements to $$$w[i]$$$ can be found by doing ternary search on the left of $$$i$$$ as well as on the right of $$$i$$$ . Leftmost element will try to move to $$$n$$$ and then to $$$n-1,n-2$$$ and finally to $$$w[i]$$$ . Example : suppose $$$n = 40$$$ and array after sorting is $$$2 , 3 , 33 , 35 ,37$$$ . Suppose we are converting to $$$35$$$ . Then for $$$2$$$ and $$$3$$$ it will best to move toward $$$40$$$ and then toward $$$35$$$ . Whereas for $$$33$$$ it can move directly toward $$$35$$$.Similar explanation for the right side of $$$i$$$.

            → Reply
          • »
            »
            »
            »
            »
            »
            4 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I would welcome anyone to hack the solution.

            → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it +23 Vote: I do not like it

        The function F(X) : Min. Moves to convert all elements to X is not unimodal. Consider the following test case :

        15 15
11 13 12 3 2 8 13 6 6 11 7 7 1 1 8

        The values of F(X) are

        F(X) for X from 1 to 15

        The graph looks like this :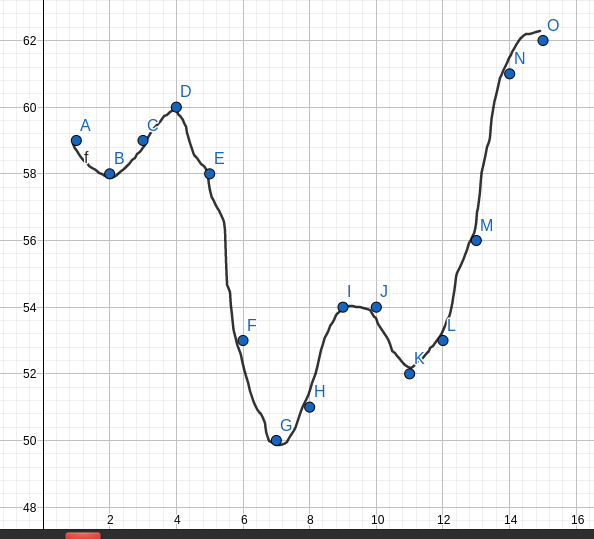

        → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    My solution for C:

    First we will calculate number of moves required for turning every lock to 1 and also calculate the number of locks whose value is increasing and decreasing. For each lock there is atmost 3 critical numbers (number of the lock, numbers which are at n/2 distance) where the increasing or decreasing nature may change.

    I inserted all critical points and sorted them and only checked the answer on the critical points.

    → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 5   Vote: I like it 0 Vote: I do not like it

    I did it with checking answers for each value in array as a assumed target with some manipulations using prefix sums and two pointers on sorted array

    My manipulations
    → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    I did it using the sliding median(sliding cost on the array of size $$$2 \times W$$$).

    Sort $$$X$$$ and consider array $$$A$$$ of size $$$2 \times W $$$ where first $$$W$$$ elements are $$$X_i$$$, and last $$$W$$$ elements are $$$N + X_i$$$. Then it reduces to finding minimum cost in CSES — Sliding Cost with $$$k = W$$$ and $$$n = 2 \times W$$$.

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      why are we pushing w elements of n+x_i?

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
        ← Rev. 5   Vote: I like it 0 Vote: I do not like it

        Since our cost function is $$$\sum{\min(|x - X_i|, N - |x - X_i|)}$$$ and it can be observed that $$$x \in X$$$.

        UPD: I'm not sure about the correctness, but I had this intuition that adding $$$N$$$ will handle this part $$$N - |x - X_i|$$$ (like the usual doubling in circular problems).

        → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      can you please provide the sliding median solution. I had the similar idea, but i needed some help

      → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    problem C without ternary search. https://pastebin.com/eX0UPCSC

    → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    i did it using binary search.
    PS.: don't know ternary search and how it works

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Not-Afraid Hey, Can you Please share your Solution as well as approach. I too tried to implement using Binary Search but I failed to do so.

      It would be helpful if you could share your Solution and your logic/some explanations.

      Thanks !!

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Note: It would be very hard for me to explain every single bit of my solution but i will try to give a rough idea.
        First let's sort the array.
        If we want to calculate answer for some index $$$i$$$: then the given array splits into three parts:
        [some_prefix] + [some contiguous subarray containing index i] + [some_suffx].
        Note: Above three arrays do not intersect, their union is equal to given array and 1st & 3rd array might be empty.
        And the idea is that all elements in 2nd array will be directly converted into $$$ai$$$. 

        for (val in 2nd array) answer += abs(val - a[i]);

        and elements in 1st and 3rd array will be converted indirectly i.e. taking them to one end ($$$1$$$ or $$$N$$$ and then taking them to $$$ai$$$).
        Now for some given $$$i$$$ you can calculate the starting and ending index of second array using binary search. The rest is just a bit of calculation using prefix sums.
        PS: You can take a look at my code at your own risk, because i overkilled it and there is a 99% chance that it will be hard for someone else to understand the code.

        → Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I did it without using ternary search. My approach was calculating number of moves to convert all elements to each x[i] and taking the minimum. For doing so, I used upper bound, lower bound and prefix-sums. I'll describe in detail if someone needs it.

    → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    O(w) solution

    1)Just make an array of 2 * w size with the value from w to 2 * w — 1 is duplicated with extra n.

    2)Now for each segment of size w find the ans assuming all elements of the segment will become equal to its median(you have to precalculate prefix sum to get sum of a segment).

    3)get the max of all ans.

    → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve D for full points?
I simply used brute force for 9 points. I thought of making a tree with its leaves representing the values on the cards and the root representing the answer(expected sum)

→ Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Overcomplicated solution, see Errichto's solution below.

    → Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it +44 Vote: I do not like it

Screencast with post-commentary and solutions, 2nd place: https://youtu.be/RpyWh424VCE (fast ABD, overcomplicated C with two pointers)

→ Reply
»
4 years ago, # |
  Vote: I like it +3 Vote: I do not like it

what was difficulty level of question in terms of codeforces ratings.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The random test file generated by me for debugging my C solution with 2 binary searches.

Tests
Answer
→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thank you for these tests!!! My solution was failing only for testcase 26 of yours , corrected it and my solution got accepted :P Btw how did you generate these test cases?

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Just wrote these random generator in some minutes and then saved the output of this in a file.

      generator
      → Reply
»
4 years ago, # |
← Rev. 4   Vote: I like it +14 Vote: I do not like it

My video editorial for the round: Google Kick Start Round G, 2020: Editorial
rough notes used: google doc notes

Proof for Problem 3, Set: 2
Initial wheel values(V) = {v1,v2,v3....vw}
Claim: it is always possible to get the optimal solution by only trying out the values v1,v2,v3...vw.
Assume that value x = p gives a better solution and p does not belong to V.

This means we bring all the wheels to the position p and cost is minimised on doing so.

We have the following scenario:
v1...v2... ... vi....p...v(i+1)... ...vw

Now all wheels will reach p by either moving forward or backward.

Let's say x1 wheels approach p from the left of it and x2 wheels approach p from the right of it.

If x1 < x2
We can obtain a better answer by shifting x=p to x=v(i+1)
On similar lines if x1 > x2 then move x to x= vi
If x1=x2
It would make no difference to the answer even if we move it to either vi or v(i+1)

Hence a better answer cannot be obtained at a value x = p such that p does not belong to V.

Let me know if this makes sense.

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it -6 Vote: I do not like it

Problem A:

My code:

~~~~~

code

It was giving WA. Any idea? I could not figure it out.

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    You should increase pos by 3 when checking string "KICK" because KICK string can overlap like "KICKICK" in this case you will skip the second string KICK

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank You very much for replying. Now I got it.

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        btw your corrected code with pos+=3; should give TLE. but because of only 2 test sets google can't have 100 testcases with same string.

        with below input your code will give TLE.

        100 testcases with same strings of length 10^5. KICKSTARTKICKSTARTKICKSTART...(upto 10^5 length). your ki and st vectors will be of lengths (10^5)/9. so total time complexity of each test will be around 10^8. so total time will be 10^10. which will give TLE

        → Reply
»
4 years ago, # |
  Vote: I like it +56 Vote: I do not like it

The last problem (Merge Cards) can be solved in $$$O(N)$$$ instead of $$$O(N^2)$$$, and it's pretty simple.

There are $$$N-1$$$ possible bars (splits) between the $$$N$$$ elements, and the described process just removes bars in random order. When a bar is removed, the score increases by the sum of elements up to next existing bar on the left and on the right. We add element $$$a_i$$$ to the score when removing bar between positions $$$j$$$ and $$$j+1$$$ if and only if all bars between $$$i$$$ and $$$j$$$ were already removed (assume $$$i \leq j$$$). One bar is last among $$$j-i+1$$$ bars with probability $$$\frac{1}{j-i+1}$$$ so we increase the answer by $$$\frac{a_i}{j-i+1}$$$. Iterating all pairs $$$(i, j)$$$ is $$$O(N^2)$$$, and we get rid of iterating $$$j$$$ by precomputing harmonic sum $$$\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \ldots$$$.

code (20 lines)
→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Since no one has answered this question above, I am asking you can you tell us what was difficulty level of problem C and D in terms of codeforces ratings?( this would help me in practice)

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      You can do the comparison yourself. Either by seeing how complicated topics and solutions are, or by seeing how many people solved it or how quickly people in the top got AC. Then tell us here what difficulty it is.

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I was able to solve testset 1 and 2 for problem C but couldnt solve its testset 3, So I think testset 3 difficulty was somewhat around ummmmm.... ~1800(maybe)? And D ~2100? I dont know if its correct or not, Its been 2 months since I started CP thats why I wanted to ask form an experienced guy.

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          In Global round 11, C was solved by 1.3k people and it's rated 2000. So i think test case 3 of C deserves at least 2100+. In terms of difficulty as well i'd say.

          → Reply
          • »
            »
            »
            »
            »
            »
            4 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I solved testcase 3 of C, and i have full confidence in myself that i can't solve 2100+ rated problem in a contest.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              4 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Yea same here... Although i took abt an hour for c but did solve it.. It feels more like a 1700-1800 problem

              → Reply
            • »
              »
              »
              »
              »
              »
              »
              4 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              I don't agree with that logic. Maybe you did it now for the first time, you never know. Edit: the problem rating on CF depend on the previous problem difficulty in the same contest so my comparison wasn't very accurate either.

              → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    I got the O(n^3) approach where we define 2 random variables X1, X2.

    Where X1 is the sum accumulated by merging [L, I] to a single element

    Where X2 is the sum accumulated by merging [I + 1, R] to a single element

    So the answer would be a another random variable X = X1 + X2 + v[i] + v[i + 1]

    By law of expectations : E[X] = E[X1] + E[X2] + v[i] + v[i + 1].

    However I did not get why your approach works, can you share the rules/laws you used to get to the result.

    → Reply
»
4 years ago, # |
← Rev. 4   Vote: I like it 0 Vote: I do not like it

Problem C , Combination Lock — Please someone help :<<<
I know it's hard to debug someone else's code... But can someone please tell me what's wrong with my code? I get TLE (I'm guessing it has to be an infinite loop). I have a deque — at every iteration I have an element which is the current option for "median" — on the left of it all the elements that are N/2 at most away from the left, and to the right of it I have all the elements that are N/2 at most from the right.
i.e if there is the following sequence 1 1 1 6 6 7 8, the maximum number is 11, and the current option is 7, the deque will be arranged as such: 6 6 7 8 1 1 1.
I believe the problem in my code is an infinite loop in the "while(straight_dist(new_first, q[0],w) > dist(new_first, q[0],w))", but I'm not sure. In that loop I pop from the front and move to the back until all elements are ordered correctly as I explained.
I have no idea how it could run infinitely as eventually I will have to get to "new_first" and then dist == straight_dist == 0 must hold! please halpppp.

** Note — I switched N and W because only a maniak would make the number of elements w and the maximum number N.
*** Another explanation I forgot: The first FOR loop checks if there is a large gap between two elements, that means that you can simply find the median and You're done.

Code - only the relevant parts (not including main and all the macros)
Full code if you want to try and submit:
→ Reply