OverKiller's blog

looking for a better solution to a dp problem
By OverKiller, history, 4 years ago, In English

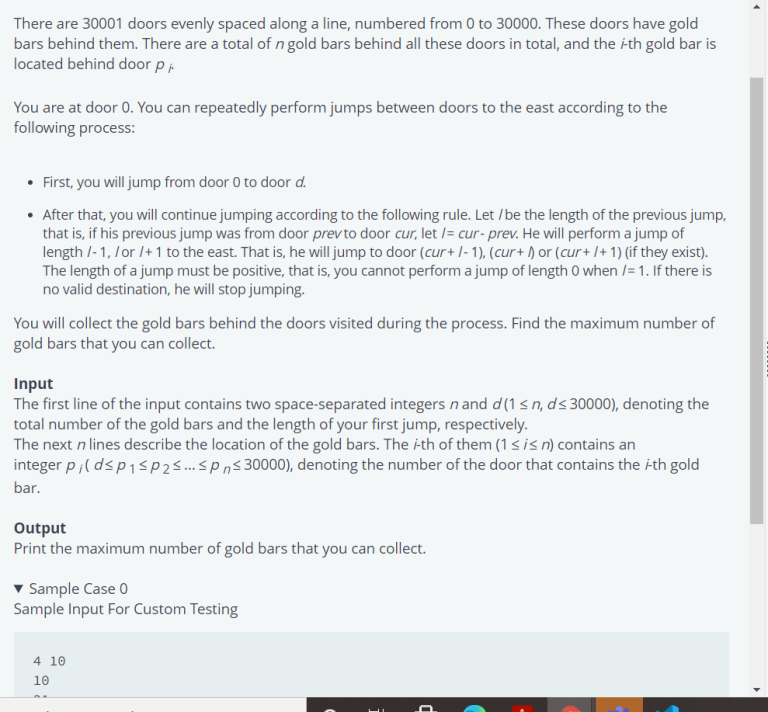
This problem appeared in a Hiring Challenge on Hackerrank and i couldn't solve it in better than $$$O(N^2)$$$ which was giving TLE. Here is the problem below:

Spoiler

I can't think of a solution better than $$$O(N^2)$$$. Any help/hints will be appreciated.

  • Vote: I like it
  • -19
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
4 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Consider, that you will never be able to make a jump larger than $$$O(\sqrt{n})$$$. Using that, you can solve in $$$O(n\sqrt{n})$$$

→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    makes sense. but $$$d$$$ can be greater than $$$√n$$$ ? How to handle that?

    → Reply
    • »
      »
      »
      4 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Ok I somewhat misread, but the solution remains the same. You can only make $$$O(\sqrt{n})$$$ types of jumps. So you can let $$$dp_{i,j}$$$, be the maximum gold you can get if the last jump was $$$d - offset + j$$$. offset should be somewhere around $$$2\sqrt{n}$$$, and $$$j$$$ should be from $$$0$$$ to $$$4 \sqrt{n}$$$.

      → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Also can anyone tell me why am i getting downvotes? i am just curious to know.

→ Reply