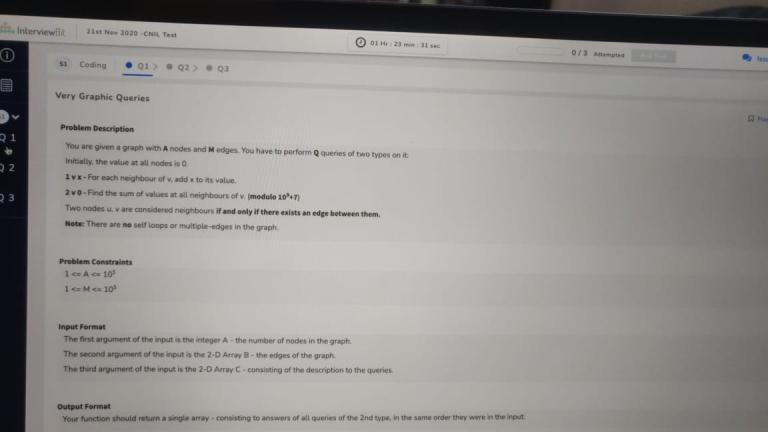
The above image is a problem from a recent hiring test by CodeNation. Any clues on how to solve it?
P.S. This test is over, it's been a couple days now
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |

The above image is a problem from a recent hiring test by CodeNation. Any clues on how to solve it?
P.S. This test is over, it's been a couple days now
| Name |
|---|



Don't ask questions about running contests/hiring tests.
It was a hiring test held a few days ago on 21st November, it's over.
I'll clarify this in the post. I thought it was clear form the word recent
I tried sqrt root decomposition but got MLE. Anyway here is my idea:
Consider vertices with degree $$$> \sqrt{n}$$$ heavy. We create array $$$sum[v]$$$ for light nodes that stores value on node $$$v$$$, and for heavy nodes, $$$neigh[h]$$$ to denote lazy share to neighbors, $$$ans[h]$$$ — contribution for second query from light nodes (as second neighbor), and $$$cnt[h][v]- $$$ number of common neighbors between $$$h$$$ and $$$v$$$, note that it can be precomputed for all $$$sqrt(n)$$$ heavy nodes using dfs.
Type1 Queries: If the vertex $$$v$$$ is light, then simply add $$$x$$$ to all it's neighbor's $$$sum[]$$$, and for each heavy node $$$h$$$ add $$$cnt[h][v] * x$$$ to $$$ans[h]$$$. Otherwise if the vertex is heavy just add $$$x$$$ to $$$neigh[v]$$$.
Type2 Queries: If the vertex $$$v$$$ is light, then iterate through all its neighbors and add their $$$sum[]$$$. Also for each heavy node $$$h$$$ add $$$cnt[h][v] * neigh[h]$$$. On the other hand, then just add to $$$ans[h]$$$ $$$cnt[h][v] * neigh[h]$$$ for all heavy nodes.
That's an interesting solution. I guess the MLE is because you can use $$$O(N^2)$$$ memory?
No, I tried allocating just an array of size $$$10^6$$$ and it got MLE too.
Actually, I think it may not blow up to $$$O(N^2)$$$ memory. I think the worst case is a complete graph, which would be $$$O(N)$$$ for the $$$cnt$$$ array. Not sure if there is any real proof of this though. Perhaps your solution was just at the edge, or needed some optimizations.
I don't understand why you think it'll blow up. It takes exactly $$$O(n\sqrt{n})$$$ memory for storing $$$cnt[h][v]$$$ and takes $$$O(\sqrt{n})$$$ time per query.
You're right, it does not blow up. A misunderstanding on my part.
I believe you are wrong about $$$\mathcal{O}(\sqrt n)$$$ part. If the bound for a vertex being heavy is $$$\sqrt n$$$, then you can have $$$\Omega(\frac{E}{\sqrt n})$$$ such vertices, which can be big. The bound should be $$$\sqrt E$$$, and then you would have $$$\mathcal{O}(\sqrt E)$$$ complexity for a query, and $$$\mathcal{O}(E \sqrt E)$$$ memory usage.
Did you try using a constant threshold for degree instead of $$$\sqrt {n}$$$ ? May be that could have helped.
Yes. I tried optimizing it in all the ways I could but as I said it even MLE'd on declaring an array of 10^6 ints.
a problem that uses a similar idea is problem E from AMPPZ 2019 (a Polish ICPC contest [i'm not really sure if this is a regional contest or what])
I've never seen any company with such difficult "hiring test" questions.
Anyways, a solution similar to fugazi's should work, as long as the constant factor isn't too high. I'm not if it can be improved to be better than square root, though.
They're well known in India for having tests that are challenging for even Div 1 participants. Not sure what the goal is with that, but the problems are interesting and fun.
In case you're interested, here are the other two questions they asked (I haven't tested my solution ideas, they may be wrong).
Given two numbers A and B, 1<=A<=B<=1e9, find the number of special numbers in the range A to B inclusive. A number is called special if the sum of pairwise product of digits is prime. For example, if the number is "abc", then the sum of pairwise product of digits is a*b+b*c+c*a.
Digit DP, the dp state is on the current number of digits, current sum of digits (which is at most 90), and the current pairwise product (which is at most 9C2*81).
Find the expected number of segments in a string of length A in a language having alphabet size B. A segment is defined as the maximum contiguous substring containing the same character. For example, "10011" has 3 segments: "1", "00", and "11".
It reduces to 1+the number of positions such that A[i]!=A[i+1], which can be worked out with math, the final answer will be something like 1+(A-1)*(B-1)/B.
Yeah codenation tests are much tougher than usual.
Once when I wrote a test from the same company, there was a question... You have 2 sequences of length 10^5 each and the second sequence has all distinct elements. You have to find the LCS (longest common subsequence).
I solved it but it's much tougher than usual hiring tests.
What's the approach of the problem?
Consider first sequence as A and second sequence as B. map i_th element of second sequence(B[i]) with i [for 1 <= i <= n(means consider B[i] as i)]
now replace every element in A with it's mapped value. if some A[i] doesn't have any value to be mapped then replace it with some small constant value.
Now LCS = length of longest increasing subsequence in A. [ strictly increasing ] Time Complexity — nlogn
Yes that is exactly what I did.
This was most likely the last question of the round which is usually completely irrelevant to qualifying. For reference when I gave their internship test the coding round had 3 problems, the 3rd was a somewhat interesting DFS order LCA problem, I couldn't handle an overcounting case and just submitted the obvious idea using all pairs LCA for partial points and still easily qualified. If I'm not mistaken in that test those who didn't even attempt that specific question still qualified if they got the other two problems (easy greedy problem and a slightly tricky (1700ish) prime factorization or dp + combinatorics problem).
So while they usually have at least 1 2000+ rated question just solving the 1800 or below rated questions is usually enough to qualify.
Actually the main point is just to filter because so many people are there in test, rest after qualifying they will conduct one 30 min telephonic round which is totally based on your projects and then rest interview rounds are normal like 1600-1800 guys will qualify easily, and final round is in depth project discussion, most people who got rejected are those because of their projects but not due to cp skills.
Was this an offcampus hiring drive? Or it was oncampus?
"On campus" placements at BITS Pilani