cniks117's blog

9D how many trees?
By cniks117, 12 years ago, In English

can some1 explain me the two test cases of this question.. http://codeforces.net/problemset/problem/9/D..

Tags dp
  • Vote: I like it
  • -4
  • Vote: I do not like it

Comments Comments (2)
| Write comment?
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

On the first sight I thought there is a problem which requires 9-Dimensional Segment Trees. LOL :D

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

First of all, your link to the problem isnt correct. I think you meant this.The task in simple english is :

Given n ( no. of distinct nodes) and h (the minimum height) , you need to print the number of binary search trees possible. For sample case 1, the no. of distinct nodes is 3 and the minimum height required is 2. So the following 5 BST are possible.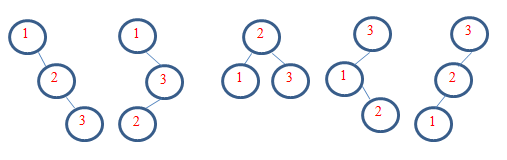

I hope the problem is clear now.

→ Reply