Hello, Can we find for example each red node (in picture blow) in O(1)?
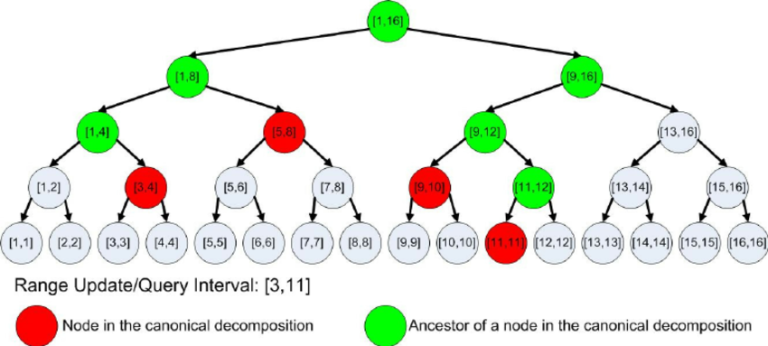
I try hard to find a way such as binary operations to get my ans. but i can't :(
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Hello, Can we find for example each red node (in picture blow) in O(1)?

I try hard to find a way such as binary operations to get my ans. but i can't :(
| Name |
|---|



Yes, somewhat, if N is a power of two. It's quite difficult to explain, so I'll show it for example with
n=16for query [2;10] in zero numeration (as in your picture).Let
landrbe the left and right bounds (inclusive) of the query, from 0 to N-1. Then the most significant set bit ofl ^ rshows you where the query gets divided for the first time. Then you can split your query into two queries:l..m-1andm..r. Example:l ^ r = 8. The highest bit is 3, which means the query splits at level 3 counting from bottom, i.e. at the first level. After that the query is split to2..7and8..10,m=8.Then you can check the least significant set bit of
lto find the level of the most left red node. Example:l=2, the lowest bit is 1, so 1 row from bottom. It can then be shown that all red nodes for queryl..m-1are returned by the following simple iterative algorithm: start withvequal to this this red node, returnv, then setv=(v+1)/2(assuming nodes are numbered top-bottom then left to right, with the root being 1). Repeat until you reach the end of the query. In other words, we take the first red node, then the parent of its right neighbour, then the parent of its right neighbour, etc. Example:l=2, m=7, we start with node [2;3] with ID 9. Then we switch to node with ID (9+1)/2=5, i.e. [4;7]. It's the last red node for this query because its right bound is exactlym-1.Do the same for the right query (
m..r), except checking the least significant unset bit ofr, and using iterative formulav=v/2-1. Example:r=10, the least unset bit is 0, so we start with the node at the very bottom for range [10;10] with ID 26. Then switch to node 26/2-1=12, i.e. [8;9]. Its left bound is exactlymso we stop here.Surely this does not look like a $$$\mathcal{O}(1)$$$ algorithm because of the iterative formula, but it's a very simple loop with absolutely no conditions, and the indexes can be evaluated in parallel, so if you have AVX, or even better AVX2 with gather-scatter, you may be able to make the fastest segment tree in the world!
I have implemented this algorithm for sum query (it can be extended to min/max and others too). It's 14 times faster than the standard segment tree and 4.5 times faster than the bottom-up segment tree on Codeforces.
UPD: For min query: 20 times faster than standard, 5 times faster than bottom-up.
thank you very much, can you please give us your source codes?
I will publish a post, hopefully today.
Here we go: https://codeforces.net/blog/entry/89399
Yes, this is possible. Take a look at the code in the Efficient and easy segment trees blog post: to get the half-open interval $$$[l,r)$$$, run
This isn't strictly speaking $$$O(1)$$$ per vertex because of the
if (l&1)condition, but you can easily make it $$$O(1)$$$ per vertex by using__builtin_ctzto skip to the next iteration that satisfies the condition.My segment tree code is all based around this bottom-up/iterative traversal: https://github.com/ecnerwala/cp-book/blob/master/src/seg_tree.hpp
thank you very much, I understand what you say, but would you please implement it(i mean that better version with
__builtin_ctz).Take a look at https://github.com/ecnerwala/cp-book/blob/88eb7d5410d90ea214a1d01807b362b82aa1696b/src/seg_tree.hpp#L95
Unlike imachug above, I found this to be slightly slower than the normal bottom-up code, though I haven't benchmarked it very carefully. I'm a little skeptical of 5x gains. On random intervals, you only get to skip 1/2 the intervals, and I think the overhead is higher with ctz, and it might hurt the prefetching.