td,dr: A1 800, A2 1500, B1 1500, B2 1700, B3 2000, C1 1900, C2 2100, C3 3000. You needed around 2000 rating to have a 50% prob of advancing to round 2.
Hi everyone. GCJ round 1A took place yesterday. If you didn't participate, you may be wondering how hard it was, and what are your chances to pass round 1B or 1C and qualify for round 2.
I provide below my estimate of the difficulty of the problems. The data and methods are the same I described in my previous post. I am sure there is room for improvement, so again I welcome any feedback.
Method 1: The 50% Bucket
Approach and Data
Please see my previous post for an explanation. In short, I use the fact that you have a 50% probability to solve a problem with difficulty equal to your rating. I divide the contestants into buckets of rating, wide 100 points, and I check for which bucket 50% of the coders solved the problem.
Out of around 10'000 participants of GCJ 1A, 3'915 had a CF namesake. I cleaned up a few obvious outliers, and the results are below.
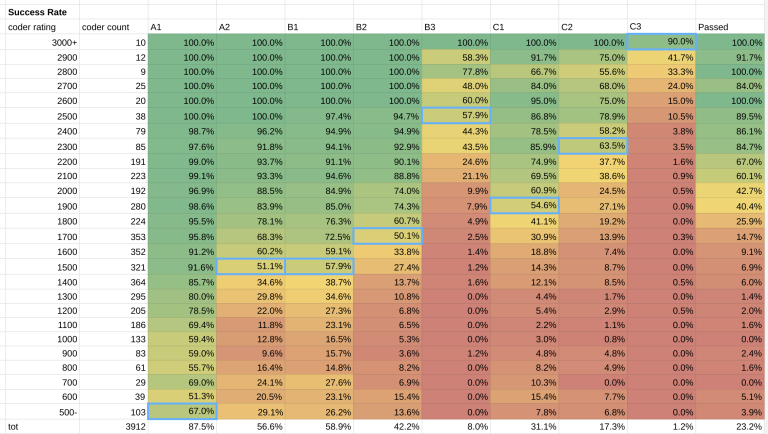
Results
This is the estimate: A1 500, A2 1500, B1 1500, B2 1700, B3 2500, C1 1900, C2 2300, C3 3000.
I think this approach is now working better than it did for the qualification round. One possible reason is that this time everyone tried to solve every problem, differently from the qualification round where there was little incentive to solve everything.
However, one problem persists: among lowly rated participants there are coders performing very well, maybe too well, for their rating. These may be new accounts of seasoned coders. The high percentage of low-rated coders who solved A1 shrank its estimated difficulty. Was it really a 500 difficulty problem? Maybe it was something more.
Method 2: Inverse Prob Function
Approach and Data
Again, please see my previous post for more details. In short, CF rating system assumes that your chances of solving a problem are a function of your rating and of the problem difficulty, see here.
We can invert the probability function to estimate the problem difficulty: $$$D=400 \cdot \log_{10} \left( \frac{1-p}{p} \right) + R$$$
where $$$R$$$ is the rating of the participants I am considering, and $$$p$$$ is their probability of solving a problem, estimated with the percentage of participants who actually solved it, and $$$D$$$ is the estimated difficulty.
In this round, the average contestant rating was 1594. I used the rating buckets around the average, from 1500 to 1700. This includes about 1000 contestants.
Results
This is the estimate: A1 1154, A2 1529, B1 1505, B2 1689, B3 2299, C1 1825, C2 1981, C3 2804.
The results are fairly in line with the previous method, which is a good sign. The two biggest differences are these:
A1 has a much higher rating now, around 1100. My impression is that the approach of inverting the prob function doesn't work very well for difficulties far away from contestants' rating. I do some average between the two estimate methods to adjust for it.
C2 difficulty dropped from 2300 to about 2000. Which one is more accurate? My personal impression is that 2300 is a bit too much, but I welcome your input here.
My Estimate
I put together the two estimates above, and I get this:
A1 800, A2 1500, B1 1500, B2 1700, B3 2000, C1 1900, C2 2100, C3 3000.
What rating did you need to be to pass the round? Well, 43% of coders rated 2000 qualified for Round 2. The percentage increases to 60% for 2100 rated participants. You needed to be about a Candidate Master to have a significant chance to pass. In the table above, right-most column, you can see more details.
What do you think?
Update based on feedback
- Lowered B3 from 2400 to 2000.











C2 difficulty dropped from 2300 to about 2000. Which one is more accurate? My personal impression is that 2300 is a bit too much, but I welcome your input here.C2 could be passed just by outputting one of these four:
Whichever one yields highest score: $$$\;S_1,\; Q-S_1,\; S_2,$$$ or $$$\;Q-S_2$$$
I wonder why even 2000 rating for this? I found problem B2 to be much more sophisticated compared to this one. Although number of successful solves were more, still seemed harder compared to the idea used in C2
However I used bitmasks and meet in the middle but finally got TLE on C2.
Oh I see. It must be good reflexes to see $$$N=40$$$ and try "meet in the middle" :D
I did the same, thinking of the complexity as $$$O(t \times 2^{\frac{q}{2}})$$$ forgetting that it was actually $$$O(t \times 2^{\frac{q}{2}} \times q)$$$ which would certainly TLE. Seeing the constraints and thinking based on that was the biggest trap in this question.
C2 is a funny kind of question. The difficulty is certainly not in the implementation, that much is clear. It's 'easy' when you know, but it's also very easy to miss.
I say it's a funny kind of question because you can have a hunch without proving it and therefore get it right without fully understanding why — Google usually tries to avoid these questions as far as I know, so I'm quite surprised they offered up 14 points for C1 and C2 combined.
The difficulty ratings of questions have always been based on correct solves, though. I think the positioning of questions almost certainly influences this. If questions C1 and C2 had been A1 and A2, they probably would have had more solves, because people would have perceived them as easier, seen higher solve numbers, and assumed that their trivial hunch was correct. The same is often true in Div 2 rounds — I find out that problem E was accessible, but I did not prioritise it because I perceived it to be difficult. It is solved by fewer people than perhaps a more difficult problem D, and therefore is officially deemed more difficult, but in practice this is not necessarily the case.
Nice numbers! What to expect from the next two qualification rounds. Since 1500 of the better coders do not participate again it should become less hard to qualify?
Thanks for the detailed breakdown. Hope you will also post the breakdowns for round 2 and round 3. I want to see the effect on the qualification difficulty when the top 1500 coders from the previous rounds will not be eligible anymore.
I solved B3 during the contest, so it can't be as difficult as 2300-2400 lol. Just one small observation and you're good, 1800-1900 at most.
I think the latter was the case here as well. People saw that A2+B2+C2 is enough to advance, so what's the point to try B3? Especially if you're sleepy (it was like 3AM in EU)
Yeah, I solved A, B, and C1 relatively quickly and basically lost incentive to code up C2/C3 even though I had sol paths. I ended up just watching the scoreboard and eating dinner during the contest.
2300 for C2 is definitely too high, should be around 2000. My first intuition is simply to output the answer of the student with the higher score, then it took me such a long time to find that it may be better to complement the answer of questions that have the same answer of the two students. I may get a chance to solve B3 if I didn't waste too much time on C2. My rank was below 1500 before points were revealed and increased by few hundreds only due to the points of C2 which surprised me.