I have been studying the Rabin-Karp algorithm for string matching lately, and I am impressed with its simplicity and average efficiency. I learned that its best-case complexity is O(n), and that its worst-case complexity is O(nm). I would like to find a way to eliminate this worst-case scenario, but have an error probability. If the error probability is low enough, then I will be able to use it and assume that the result will always be correct (unless I'm extremely unlucky). Below there is some pseudocode which implements the rabin-karp algorithm:
1| rabin-karp(text, pat) {
2| n = size(text), m = size(pat);
3| text_hash = hash(text[1..m]), pat_hash = hash(pat[1..m]);
4| for i=1 to n-m+1 {
5| if text_hash = pat_hash
6| if text[i..i+m-1] = pat // this step takes O(m) time
7| print "Index: " i;
8| text_hash = hash(text[i+1..i+m]); // this is computed in O(1)
9| print "done";
To achieve my goal, I have to eliminate line six. To be able to do that, I need to be sure that this will not affect the correctness of the algorithm too much. In other words, I need to be sure that my hash function will be good enough to make the error probability low, but I can't come up with something clever. Could somebody help me? Thanks in advance.











Correct me if I am wrong!!!
What about generating many(lets say 10) different completely different hashes (by choosing different bases and mod values) for pattern and texts. If all 10 hashes are equal for some substring of text and the pattern, then there will be high chances that they are same.
Additionally to be completely sure that there is a possible match, you can run a O(m) loop to verify that. Now the chances that all 10 hashes are same are rare and the verification step is carried on with very less probability.
Here's the code for 2 different hashes for clarity
Thank you very much. That's really interesting. I will definitely give it a shot.
I think there's a small mistake in line 3 of your pseudocode: text_hash = hash(text[1..m]) (given m <= n).
You are right! Thank you for pointing this out.
All that you may need to know.
Let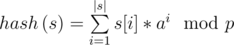
A probability of collision when checking two random strings is about
A mean number of collisions in a set of N random strings is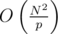
If I know your a and p, your solution is just a hundred points for me on CF. But if smb don't know that, you may assume the mean case.
You may random your hash constants, e.g. use 2 different pairs (a1, p) and (a2, p) where p = 10^9+7 and check both hashes whether them match or not.
Thank you very much!
You can use a 2^64 as your mod, so you can even get rid of the % on the code using just unsigned long long int. I don't know how to prove it, but the guy who taught me this hash function, proved it once that the probability of having collisions with a prime base using 2^64 as its module is about 1/10⁶, so the chance of hitting a collision is like winning on the lottery.
I've never had a problem using this hash function, so for me it's quite safe using it.
Never use 2^64 as mod, as there are well-known universal collisions for it. E.g. first 2^n of http://oeis.org/A010059 and http://oeis.org/A010060 have the same hash functions when n >= 11.
Use a different number for mod (i.e (10^9 + 7)) would solve this problem ?
Well, it really depends on what number you use as a base. The guy who taught me this hash function, said that in order to avoid this kind of special collision you set some random number to add in the beginning of every number and also choose some magic prime bases. Actually once I had a problem in Codeforces using 2^64 as mod, but then I changed the base 33 to 77 and got AC.
It DOESN'T depend on what number you use as a base.
If the base doesn't matter, take a look at these solutions:
Using 47 as base = WA => http://codeforces.net/contest/271/submission/3126158
Using 43 as base = AC => http://codeforces.net/contest/271/submission/3126161
And you can see that the case 41 that the first submission got WA is exactly the same as the anti-hash test. How can u explain it ?
It's true only for string's length >= 2048.