Can someone help me to deduce this?
For any numbers x,y,z:
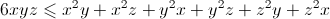
UPDATE: problem is wrong see coment.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Can someone help me to deduce this?
For any numbers x,y,z:
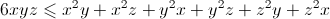
UPDATE: problem is wrong see coment.
| Название |
|---|



http://en.wikipedia.org/wiki/Muirhead%27s_inequality
http://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means
I thinking about this but,this is when x,y,z are positive other way no :(
When numbers can be negative, it's incorrect inequality. For example: x = 0, y = 2, z = - 1
you'r right,i had a mistake;
x,y,z is such numbers that in this numbers 2 of them is positive and one any number.
More formally at first i had such Inequality(where a,b,c>0):
than mentioned x=b+c-a,y=a+c-b,z=a+b-c numbers,and get:
may say that a<=b<=c and get that x>0 y>0 z<0
now I guess that this way is difficult. can somone tell me another easy way to prove first Inequality?
This is a well-known inequality, http://en.wikipedia.org/wiki/Schur's_inequality
It is equivalent to the following: (a + b - c)(b + c - a)(a + c - b) ≤ 3abc, so when one of the brackets is negative, left part of inequality is also negative, when the right part is always positive.
thanksss bro :)