Can someone help me to deduce this?
For any numbers x,y,z:
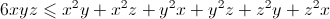
UPDATE: problem is wrong see coment.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Can someone help me to deduce this?
For any numbers x,y,z:
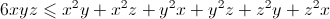
UPDATE: problem is wrong see coment.
| Name |
|---|



http://en.wikipedia.org/wiki/Muirhead%27s_inequality
http://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_geometric_means
I thinking about this but,this is when x,y,z are positive other way no :(
When numbers can be negative, it's incorrect inequality. For example: x = 0, y = 2, z = - 1
you'r right,i had a mistake;
x,y,z is such numbers that in this numbers 2 of them is positive and one any number.
More formally at first i had such Inequality(where a,b,c>0):
than mentioned x=b+c-a,y=a+c-b,z=a+b-c numbers,and get:
may say that a<=b<=c and get that x>0 y>0 z<0
now I guess that this way is difficult. can somone tell me another easy way to prove first Inequality?
This is a well-known inequality, http://en.wikipedia.org/wiki/Schur's_inequality
It is equivalent to the following: (a + b - c)(b + c - a)(a + c - b) ≤ 3abc, so when one of the brackets is negative, left part of inequality is also negative, when the right part is always positive.
thanksss bro :)