sillycross's blog

Doubts on Round #211 ( Div 2 ) Problem E
By sillycross, 11 years ago, In English

I doubt whether the standard solution for problem E is correct.

The problem is: when two center's distance is smaller than 2R, the two circles may still be separated on the grid matrix.

Consider the following case:

Circle 1: center (0,0) radius 14

Circle 2: center (20,19) radius 14

The eculid distance between center is 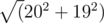, which is less than 28.

However, the 2 circles do not intersect on a grid matrix, since no integer coodinate falls on their intersection area. So the 2 circles are still valid solution.

But it seems that the standard solution did not consider this special case. I (and many others) got wa on test 20. After I changed the intersect checking to "center distance<=2R" it got accepted.

solution: http://codeforces.net/contest/363/submission/5067126 notice the quoted code between line 77 and 82. after removing these codes the solution got WA.

A possibly wrong test case for the std solution: http://paste.ubuntu.com/6399141/

  • Vote: I like it
  • +16
  • Vote: I do not like it

»
11 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Thanks for your post. I also have the same opinion with you on this issue (but it seems you made some typos in your reasoning). It should be when the distance between 2 centers is less than or equal 2R, the two circles may still be separated because the set of covered cells is smaller than the original circle.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    eh, you are right. I mistyped.. Thank you, already edited.

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I also doubt it.

→ Reply
»
11 years ago, # |
← Rev. 5   Vote: I like it +11 Vote: I do not like it

This is a simple example:

R = 2

Center 1 at (3, 3) and center 2 at (6, 5). Distance is sqrt(3 * 3 + 2 * 2) = 3.6 < 4 = 2R

..x....
.xxx...
xxxxx..
.xxxo..
..xooo.
..ooooo
...ooo.
....o..

→ Reply
»
11 years ago, # |
  Vote: I like it +2 Vote: I do not like it

We are investigating the situation.

→ Reply