That's a part of final editorial. I'm sorry for delay. Please, report me about mistakes and unclear moments in solutions and in my english.
A div2
Task was to find the least digit, that is not contained in the given number and compare with given k.
B div2
Good sequence may contain only zeroes or contain some positive number. In the second case such a sequence is not longer than sequence {0, 1, 1, 2, 3, 5, 8, ..., x, y} where y > 109 and x ≤ 109. That's possible to find it using dummy algorithm. In the first case you may use binary search of two pointers.
A div1
Let's notice that sum in the rectangle (x1, y1, x2, y2) is sum(x1, x2)·sum(y1, y2). Where sum(l, r) = sl + sl + 1 + ... + sr. Then, we have to calc sum(l, r) for every pair (l, r) and count how many segments give us sum x for any possible x (0 ≤ x ≤ 9·|s|). In the end we should enumerate sum on segemnt [x1, x2] and find 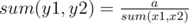 . There is corner case a = 0.
. There is corner case a = 0.
B div1
We may assume that John may exchange any subset of his items x to any other subset y, such as s(x) + d ≥ s(y) (it does not matter if x intersects y). We can find all possible sums in subset of elements of the given set of items using standard dp (knapsack problem). John should always exchange all his current set of items to another, because if he had exchanged some subset of x (current set) z to y, we can say that he had exchanged x to 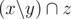 . So, we have to find shortest sequence of sets a, such as s(ai + 1) - d ≥ s(ai) for any possible i and a0 = {}. This subtask could be solved using following greedy algorithm. ai, i > 0 is maximal correct sum such as ai ≤ ai - 1 + d. Consider optimal answer c and our answer a. Let k is the first position where ak ≠ ck obiviously ak > ck (because ak selected as maximal as possible). Then consider q such as qi = ci for i ≠ k and qk = ak. q is either optimal. Applying similar operations we will obtain a. So, a is optimal.
. So, we have to find shortest sequence of sets a, such as s(ai + 1) - d ≥ s(ai) for any possible i and a0 = {}. This subtask could be solved using following greedy algorithm. ai, i > 0 is maximal correct sum such as ai ≤ ai - 1 + d. Consider optimal answer c and our answer a. Let k is the first position where ak ≠ ck obiviously ak > ck (because ak selected as maximal as possible). Then consider q such as qi = ci for i ≠ k and qk = ak. q is either optimal. Applying similar operations we will obtain a. So, a is optimal.
C div1
We expected many unproved, but tested solutions. I think that careful prove of my solution with pen and paper is very difficult. So I will use some statistic-based facts.
- Consider the set of divisors of number k. One can check that it's beautiful set.
- If factorisation of k has the form
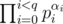 where αi ≥ 3 and pi is distinct primes, set of divisors of k which is less than
where αi ≥ 3 and pi is distinct primes, set of divisors of k which is less than 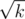 is also beautiful.
is also beautiful. - How to prove item 2? Consider set A of pairs of divisors of k (ai, bi) such as ai·bi = k and ai < bi. Obiviously (if k is not complete square) any divisor will be contained only in one pair. It's easy too see that
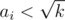 . Consider some element of factorisation of k pα such as
. Consider some element of factorisation of k pα such as 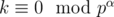 and it is not true that
and it is not true that 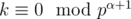 . Let f(x) is maximal number s such as
. Let f(x) is maximal number s such as 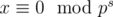 . f(ai) + f(bi) = α. For every q such as
. f(ai) + f(bi) = α. For every q such as 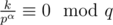 numbers q, q·p, ..., q·pα will be divisors of k. That implies that
numbers q, q·p, ..., q·pα will be divisors of k. That implies that 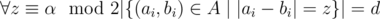 where d is number of divisors of
where d is number of divisors of 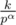 . So in
. So in 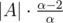 pairs both numbers are divisible by p. So set {a0, ..., a|A|} is beautiful.
pairs both numbers are divisible by p. So set {a0, ..., a|A|} is beautiful. - But there are some pairs with f(ai) = α.
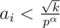 is equivalent approval.
is equivalent approval. - It's always possible to find such k as number of it's divisors is bigger than 2·w where w is number of elements in required set. You may write following dp to find it.
- dp[i][j] is minimal k which is constructed of first i primes ans has j divisors.
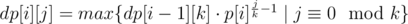
- About 10 primes is enough to cover all k.
- Now we can construct beautiful sets with more than k elements.
- Using item 4 we will understand that constructed answer is very beautiful (about 60% of elements divisible by every possible p) and we can always delete extra elements.
Last items is not strict, but one can check it with his computer.
D div1
- Consider random element ar of a. With probabillity

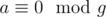 where g is ghd of a.
where g is ghd of a. - Let xi = gcd(ai, ar). There are no more than d distinct xi where d is number of divisors of ar.
- We can find number of ai such as
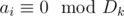 for every k in O(d2). (D is set of divisors of ar)
for every k in O(d2). (D is set of divisors of ar) - Repeat item 1 x times we will get correct solution with probabillity 1 - 2 - x.
There is the way to solve this problem O(n·plog + d·2plog) for iteration where plog is the maximal number of distinct primes in factorisation of ar.
E div1
- Let's find number of rectangles whick consist k ones and intersect
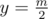 in cartesian coordinate system.
in cartesian coordinate system. - It's possible to do it in n2·k. We need to find closest k ones on the top and on the bottom of the
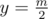 and enumareate all segments [l, r] such as 1 ≤ l ≤ r ≤ n and find closest k ones on the top and on the bottom of the segments merging results for rows.
and enumareate all segments [l, r] such as 1 ≤ l ≤ r ≤ n and find closest k ones on the top and on the bottom of the segments merging results for rows. - If we have k closest ones on the top and on the bottom of the segment we will find number of rectangles consists k ones and cross
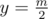 on [l, r] in O(k).
on [l, r] in O(k). - Then we should find number of rectangles, which don't cross
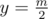 . Let's rotate table by 90 degrees, solve similar problem for two halfs of the table and so on.
. Let's rotate table by 90 degrees, solve similar problem for two halfs of the table and so on. 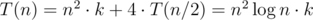 for square-shaped tables.
for square-shaped tables.

At the picture 1 two closest ones on the top (black cells) lying on the 4'th and 2'nd horizontals. Closest ones on the bottom lying on the 5'th and 7'th. Then if k = 2 there are zero correct rectangles with two "ones" on the tom. There are four rectangles which consist one "one" on the top and one "one" on the bottom. You can see how segment grows up at the pictures 2, 3 and 4. Every time you should merge closest k ones of the added row with closest k ones of the current segment.











Actually, the recurrence in the problem E is T(N) = O(N2k) + 4T(N / 2). The one you've provided in the editorial has solution T(N) = O(N2k).
Oh, you are right, I'd been thought that it is n^2*k till sunday.
I don't know to solve when a=0 in problem A div 1??
Let f(0) be the number of substrings of the array that sum up to 0. So if 0 = a = sum(x1, x2)·sum(y1, y2), we know that at least one of the factors must be 0. I used inclusion-exclusion to compute the answer: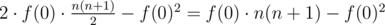 (this is the number of ways the first factor can get 0 while we don't care about the second + the number of ways the second factor can get 0 while we don't care about the first - the number of ways that both get 0).
(this is the number of ways the first factor can get 0 while we don't care about the second + the number of ways the second factor can get 0 while we don't care about the first - the number of ways that both get 0).
thank you very much !!
Can anyone explain how n*(n+1)/2 came? I am not able to understand how inclusion exclusion is working?
say , s = "102345"
matrix:
102345
000000
30____
40____
50____
x*1 size rectangles with 0 sum = 5*(5+1)/2
1*x size rectangles with 0 sum = 5*(5+1)/2
1 rect is common cell(1,1)..subtract it
you used s="10345" then made matrix according 102345 please correct it
Div1 C. (or Div2 E.), please~~
I can't find a way to prove the solution which is
Accepted.This comment
What is the c in Bdiv1? Is it the same as o is?
Can the editorial of Div1 E be more detail? Probably with a simulation of the algorithm will be better. I think this is a really good problem, and I really want to know how to solve it. Thanks the author in advance. :)
can you explain div2-C problem statement??
Well, what exactly do you need to know? The goal was to find number of all different submatrix such as sum of all its elements is equal to a. The matrix b (NxN) element (i,j) is multiplication of our string s elements i and j. I think this is almost that you need to know, but it is as well explained at original statement.
My accepted solution for DIV1-C:
Try to build answer
first, from {2, 3} primes,
then from {2, 3, 5} primes,
...,
then from {2, 3, 5, 7, 11, 13} primes.
How to try to build:
If some prime is occured less than (k+1)/2 times, then try to multiply one of the current value which is not divisible by the prime.
Six primes is enough to build answer for k = 5000.
Details: 5193128, less than 50 ms
thanks for your comment.
however, most of the codes which can solve the problem is quite short.
My code only has 51 lines, use about 15ms. // Copy from others, of course. :-(
=> http://codeforces.net/contest/365/submission/5171080
I believe there may be a more efficient way to prove that solution.
Yes, my code is not short and can be simplified. I was in hurry while writing it, and had no time for refactoring. The main purpose of my comment was to give idea about usage of no more than six primes.
My solution used 5 primes for k=5000: 5159650
There are many easier ways to solve Div2 B , and don't need to binary search.Just a simple dynamic programming .
For problem B div2 there is a much simpler way to do that by dp. for problem B div1 first part of it can be done by adding number to all previous sum we got because we can't have more than 5e5 number maximum. why making it so complicated?!
You approach for problem b div1 is similar to mine. It's not complicated, what are you talking about? What about div2 b, you are right I will add that to post.
For Div1 B, I'm just saying we can use brute force instead on knapsack. that's all. tnx for your great problems.
in problem A div 1 why maximum sum of sequence must be 9*|S|? Can anyone explain me that?
because every character of string is between 0 to 9 so the maximum sum is size of string times 9
I don't understand the proof for the C in div1, especially for the item2, can someone tell me about these ? thanks!!(sorry for my poor English)
I think you should look at example (divisors of 216)
You can see, that considered set is in the first column. 3, 6, 9, 12 are divisible by 3 and 2, 4, 6, 8, 12 is divisible by 2. So, it's beautiful set. Has it become more clear?
In div1-D, what you should say is that you compute the number of elements ai that x divides for all x which are divisors of ar, not just for all x which arise as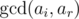 for some i. (The latter is a subset of the former.) For example, consider this testcase: 1, 1, 1, 2·3·5, 2·3·7, 2·5·7. If you pick ar = 2·3·5 for example, you must consider x = 2 (the actual ghd), which is not a gcd of any element and ar (the gcds are: 1, 1, 1, 2·3·5, 2·3, 2·5). This is of course still doable in
for some i. (The latter is a subset of the former.) For example, consider this testcase: 1, 1, 1, 2·3·5, 2·3·7, 2·5·7. If you pick ar = 2·3·5 for example, you must consider x = 2 (the actual ghd), which is not a gcd of any element and ar (the gcds are: 1, 1, 1, 2·3·5, 2·3, 2·5). This is of course still doable in 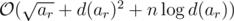 .
.
Yes, you are right, I will write this item carefully.
I think the probability-solution for the problem D-div1 isn't appreciated. Let's consider this case
I think the probability-solution will give
1but the correct answer is2Do you have any arguments? Is my calculation of probabillity wrong?
On your test my solution works with probabillity 1.
Because sometimes, gcd of two elements is not a result.
For example:
Oh, yes, I got it. I've fixed explanations.
^_^. Thus, I think you should update the test data because some wrong-solutions still got accepted :D
For example: http://codeforces.net/contest/364/submission/5199045
I think, that's correct solution. Why it's wrong?
Can anyone explain the div 1 5th problem with a picture ? since the original picture is not available now
Errichto Can you please explain your solution for div1 A ?
Do I even know this problem? :D there is no link or statement in this editorial.
Sorry I did not notice, here is the link to the Problem
In div2B, why do we need binary search? Wouldn't it be done by simple brute force?
For problem D div1 can anyone tell me how to avoid getting wa for the last test case and the specific reason why for that test case my randomized algo is not working properly? 265153694
really liked problem C