Yesterday there was a online test of some website (GeeksforGeeks) where I encountered the below problem, I was not successful in getting AC for the problem because of TLE issue, it will be very helpful if someone can share the approach or give hints to solve the problem ,below I am attaching the problem statement. My time complexity of the solution was O(N.x) where 'x' is the frequency of maximum element of the given array. 
 Any help will be appreciated.
Any help will be appreciated.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 8 | luogu_official | 150 |
| 10 | awoo | 148 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Mar/06/2025 23:14:57 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Auto comment: topic has been updated by __Tanzeel__ (previous revision, new revision, compare).
Do you have the link to the problem?
I do have one approach and want to test it.
The approach: Since we can't make any three elements a[j] > a[i] < a[k]. We're left with 2 choices, make sorted array, or reverse-sorted array. in order to create the array we can just copy & paste the given array into another variable and from the start if it's not sorted we can just modify the value. To create an increasing sorted array you have to start from the end.
upd: I just noticed there is 1 more choice. and that is to make a mountain. To do this you can just simply create dp sort of thing from the beginning and from the end. and consider each element as the peak of the mountain. And this case contains the other 2 cases.
code: https://pastebin.com/d6bFy9YH Sorry for the bad English.
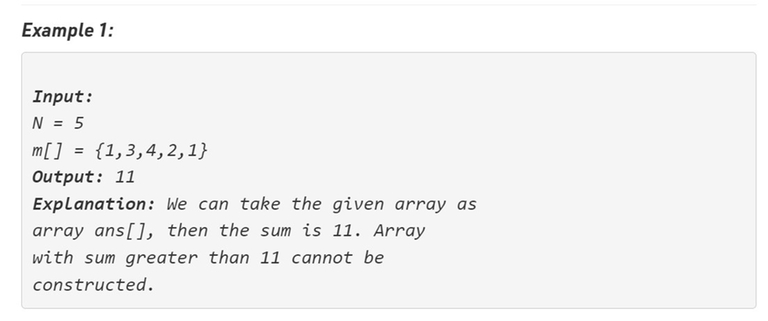
This is the link ,I think the special array should be like hill structure ,I noticed this by analyzing the test cases
As far as I understood, the problem is to find an array that is initially increasing then decreasing. So we first need to fix the pivot element i.e the highest element in the middle. Let us brute force that pivot element as the ith element. Now you need to calculate the sum of the left part and the right part.
I will explain for the left part, as calculating the right part is exactly the same. Maintain a $$$dp$$$ array, $$$dp[i]$$$ is the sum of the construction of the increasing sequence adhering to the rules $$$arr[i]<=m[i]$$$.
To calculate $$$dp[i]$$$ , let $$$j$$$ be the previous smaller element than the $$$i^{th}$$$ element (can be calculated using stack in linear time). $$$dp[i]=dp[j]+(i-j)*m[i]$$$ as all the places greater than m[i] will be occupied by m[i] itself. similarly maintain another $$$dp2[]$$$ array for the reverse array for the right part and the asnwer is just $$$max(dp[i]+dp2[i+1])$$$ for all $$$i$$$.
Thanks for explaining in detailed way :)
Monotonic Stack for prefix and suffix
...
What are the constraints?
N can range till 10^5 and elements of array are non negative and can go till 10^9