affix's blog

Greatest GCD between some numbers
By affix, 11 years ago, In English

We've got n nonnegative numbers (a[i]) . We want to find the pair with maximum gcd. For example if we have:

2 4 5 15

gcd(2,4)=2

gcd(2,5)=1

gcd(2,15)=1

gcd(4,5)=1

gcd(4,15)=1

gcd(5,15)=5

The answer is 5.

n<100,000 and a[i]<100,000

I have an O(n*sqrt(n)) algorithm is there more efficient algorithm like O(n*logn) or O(n)?

  • Vote: I like it
  • +4
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

Sorry for my bad English:)

This problem can be solved by brute force answer and counting how many numbers the answer divides.

It's O(R log R)

where R = maximum number in a[] array.

you have to make an array cnt[], which will keep the count of integers x.

cnt[x]=count of number x.

and code:

for (int i=1;i<=R;i++) {
   int k=0;//count of numbers that are divisible by i
   for (int j=i;j<=R;j+=i)
      k+=cnt[j];
   if (k>=2) ans=max(ans,i);//if count of number more than one, 
   //then we have two numbers with a divider i, 
   //and it is not necessarily maximum divisor of these numbers.
}

O(R log R), because R/1 + R/2 + ... + R/R ~ R log R

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    thank you very much!

    → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I'm trying to implement this algorithm in a problem, but I'm not as good to achieve it. Can you explain a little the part of the array of count of the integers please???, with that count array, do you mean a sieve???. Thanks in advance :)

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      cnt[] — is not sieve.

      cnt[x] — count of number x in a[]

      code which calculate cnt[] :

      for (int i = 1; i <= n; i++)
    cnt[a[i]]++;
      → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Sorry because my english ability is not good. I think that this problem can be solved by dynamic programming. We call F[i] is the number of different elements in array a which are the mutiple of i. The result is the largest integer x that F[x] is larger than 1. We can calculate F[i] by following way. First we must initial the value of array F by F[a[i]] = F[a[i]] + 1. i = p1^m1*p2^m2*p3^m3*...*pk^mk. (k <= 7 because a[i] is smaller than 100000) If we can calculate the value of F[i] then F[i/p1] = F[i/p1] + F[i]. F[i/p2] = F[i/p2] + F[i]. F[i/p3] = F[i/p3] + F[i]. ... F[i/pk] = F[i/pk] + F[i]. You can calculate p1, p2, ..., pk in O(1). You will have more details here: http://e-maxx.ru/algo/prime_sieve_linear Because k <= 7, this approach can run in O(7*maxC) with maxC is the largest value in array a. Sorry again because my english ability is bad.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Oh, i think my algorithm has some problems.

    → Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it -26 Vote: I do not like it 

#include <stdio.h>
#include <stdlib.h>  
long  i,k,n,nmax;
long  brojevi[1001];
long nzd(long a, long b)
{
     if(!b) return a;
     a%=b;
     return nzd(b,a);

}
int main()
{
 
   
    scanf("%d",&n);
   
    for(i=1;i<=n;++i)
    {
      scanf("%d",&brojevi[i]);
     
    }
  for(k=1;k<n;++k)
  {
      for(i=k+1;i<=n;++i)
      {
             if(nzd(brojevi[k],brojevi[i])>nmax) nmax=nzd(brojevi[k],brojevi[i]);
      }
  }  
 
    printf("%d\n",nmax);
    system("pause");
    return 0;
}

I think this will be helpful.

→ Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it +33 Vote: I do not like it

    Are you serious?)

    → Reply
    • »
      »
      »
      11 years ago, # ^ |
      ← Rev. 2   Vote: I like it +13 Vote: I do not like it

      ur profile picture describes my (and possibly many others') reaction after reading lovro-sinda's comment! :D

      → Reply
  • »
    »
    11 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your algorithm is so efficient you could just have used a simple cycle instead of Euclid's algorithm.

    → Reply
  • »
    »
    11 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    I have an algorithm is there more efficient algorithm like or ?

    ur algorithm is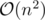 , which is much less efficient than !

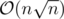    EDIT: also, the size of ur array (which, for some weird reason, is called brojevi :P) is only 1001, so ur algorithm, for large inputs, would result in RE!

    → Reply