In this post I'll try to expose the results of my research regarding the rating formula. More specifically, I'll show a graph that gives you a match rating according to your performance in a contest and some aspects of how ratings are updated. This post is quite large, if you are only interested in the results you can easily skim through it :)
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
mariabauza and I are trying to do the Travelling Salesman Problem in a segment graph (for a real life application, it's not a CP problem): you are given 10-100 segments in the plane you have to color (go through), give the shortest path to color them all.
For example, here are 2 possible paths (in red) for the same segments, one shorter than the other.
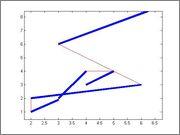
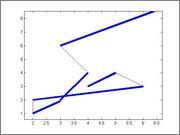
To do it we use the 2-opt algorithm we learned in Petr's blog. There he explains that the 2-opt algorithm works very well, finding the best solution in very few tries. However, with only those 5 (random) segments it only finds the optimal solution 26% of the time after 400 restarts (finding only local minimums during 400 tries, 74% of the time).
Do you think the algorithm may not be as effective for the fact we are now dealing with segments and not points? Or are you sure the algorithm should work almost perfectly and we must have some bug? (We have looked our code thoroughly before posting here, but you never know) Can it be slightly modified to work better in this kind of graph?
Finally, we know that we can develop TSP algorithms for Euclidean graphs, but the only one we know (using the MST) doesn't quite apply when dealing with segments. Do you know/can you come up with any other algorithm that could help?
Thanks!
The problem I've run into is the following:
We have a graph G in which the weights of its edges are upward parabolas varying in time. For each instant t, we could potentially calculate the Minimum Spanning Tree. Since parabolas are convex and MST(t) is a minimisation problem we can try to find the 'global' MST: from all the infinetely many times t choose the MST(t) with minimal weight.
I've found an E3·log(V) algorithm: two parabolas meet at most 2 times, thus the numbers of crossings of all weight parabolas is E(E - 1) = O(E2). At all times between two consecutive crossings the order of the edges is the same; therefore the MST will be the same. Thus, we can compute it using Kruskal in O(E·logV) and then minimize for the edges found in O(V).
Can you find a faster solution? [I don't know if it exists :) ]
Thank you!
As you know, given a directed graph there are several algorithms that efficiently divide the graph into Strongly Connected Components. Once you have them you can construct a new graph where each vertex corresponds to a SCC and there is a directed edge from u to v iff there exists an edge that goes from a vertex in SCC u to SCC v. Do you know a way to create the adjacency list of this new graph efficiently stored in a vector<vector>?
The only solution I've come up with is doing a vector<set > G and forall edge (a->b) in the old graph inserting comp[b] in G[comp[a]] and once you've done that copy the set into a vector<vector >.
Thank you!
| Name |
|---|










