Alright, so this is my 2nd post here. The 1st one, as you can see, was written in Vietnamese – my mother tounge, just because I thought that CodeForces Blog could be used for my personal purposes and my entry would not be read by anyone else, except me :D
Due to that, I’m gonna translate that post into English so that anyone can read it and leave feedbacks :) One more thing to say, *I’m not the original author of this article, I just rewrite it to understand BIT better *
PS: As I said, Vietnamese is my mother tounge, and I’m only a high school student, so sorry for my bad English. J
Advantages of BIT:
- Use less memory than RMQ
- Easy to code
- Can be used in many problems about number sequence
- Runtime: O(logN)
Disadvantages : =’= BIT is hard to understand (so that’s why I’m writing :D)
Main content:
BIT consists of two operations in an array A[1..N] of numbers
SET (index, value) : To add value to A[index] (or A[index] += value)
GET (index) : To sum up A[1]..A[index ] (or Get ≔ A[1] + … + A[index])
Details:
We know that a natural number can be expressed as a sum of the powers of 2, for example:
Example 1:
22 = 16 + 4 + 2
= 2^4 + 2^2 + 2 ^1
Applying this idea for BIT, we’re going to express the sum of A[1]..A[n] as a sum of sub arrays, each of them has 2^k elements
How to code:
S(i,j) is the sum of A[i]..A[j] (or S[i,j] = A[i] + A[i+1] +…+ A[j]). So with number 22 in Example 1, expressed as a sum of the powers of 2, is gonna be like this:
S(1,22) = S(1,16) + S(17,20) + S(21,22)
To get the positions of sub arrays, use this formula: i - i AND (-i) + 1.
Demo.:
22 - (22 AND (-22)) = 20
20 - (20 AND (-20)) = 16
16 - (16 AND (-16)) = 0
Thus, the structure of BIT T[] will be:
T[i]: Sum of S(i - i AND (-i) + 1 , i )
How does GET work?
Notice: GET (index) sums up A[1] → A[index].
Idea: To get the sum of A[1].. A[index], here we start with A[index] first. Parent of A[index] can be reached by using the following formula: i – i AND (-i)
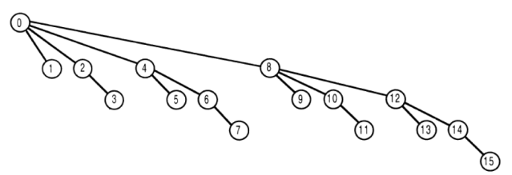
GET (T,i)
1 s ← 0
2 while i > 0 do
3 s ← s + T[i]
4 i ← i – i and (-i)
5 return s
How does SET work?
Notice: SET (index,value) adds value units to A[index]
Idea: To increase the value of A[index] with value, is to increase sub arrays which CONTAINS A[index]
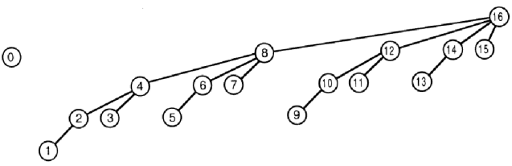
Example : We want to add 1 to A[9]. So we also have to add 1 to sub arrays which contains A[9]. Look at the image, here we have A[10], A[12] and A[16] both consist of A[9] J
So how do we find which array contains A[9]?
Use this formula: i + i and (-i)!
With this relationship, the demonstration of BIT will be opposed to the first one in GET procedure:
Pseudo-code
SET (T,i,v)
1 while i ≤ size[T] do
2 T[i] ← T[i] + v
3 i ← i + i AND (-i)









