I was shown this JOI problem by Jasonwei08 today. The problem statement boils down to:
Given an array $$$A$$$ of $$$2^L$$$ integers, $$$1 \leq L \leq 20$$$, process $$$1 \leq Q \leq 10^6$$$ queries. For each query, consisting of a length-$$$L$$$ pattern of either 0, 1, or ?, report the sum of all $$$A_j$$$ where the binary representation of $$$j$$$ matches the pattern.
For example, given the array $$$10, 2, 3, 15, 0, 9, 12, 3$$$, the query $$$?1?$$$ would match the binary indices $$$010, 011, 110, 111$$$, which are $$$2, 3, 6, 7$$$ in decimal. The result would be $$$A_2 + A_3 + A_6 + A_7 = 33$$$.
Let's start with a brute force approach. Build a perfect binary tree of all prefixes of length up to $$$L$$$, and traverse it downwards, summing the values at the leaves:
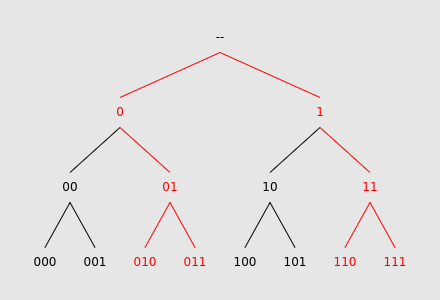
Notice that every time we "split", and take both children, the resulting subtrees are identical. We can use this to our advantage. Instead of subdividing into two separate searches, we can instead fold the two subtrees together, adding together the values at the leaves.
This optimization reduces the number of nodes traversed from $$$O(2^L)$$$ to $$$O(L)$$$, though processing each node isn't as simple anymore.
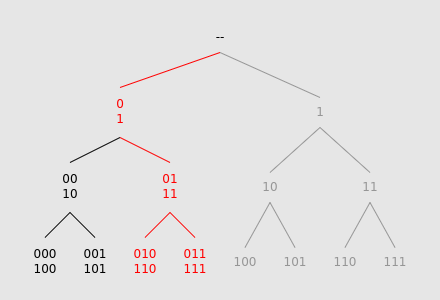
We can implement this by maintaining an initial array containing all of the values of the leaves, and at each tree-descent step, we create a new array by either:
- if we descend to only one child, cut the array in half and pick the appropriate side.
- if we split to both children, cut the array and overlay the two halves over each other, adding them together.
At the end, we obtain a length-one array whose only element is equal to the sum of all matching leaves.
This requires $$$O(2^L)$$$ space and time per search, which doesn't seem to be any better complexity-wise than brute force. However, we can now leverage another datastructure: a trie.
By building a trie out of all of the patterns, we can then run a downward search through the trie, at each step maintaining the array of remaining leaves. A depth-first search is ideal for this, as it guarantees that only one node at each depth can be processed at a time, and therefore provides a bound on memory usage.
Unfortunately, for this specific JOI task, the memory limit is too tight for a normal trie to work, even with very aggressive modifications. jay_jayjay suggested I sort and divide-and-conquer over the patterns as a sort of 'virtual trie', which worked!
(The intended approach to this task was in a very different direction, using SOS. Mine isn't even a very good one, I just thought the technique was cool.)
More generally, this works not only on binary strings, but on any pattern with a sufficiently low number of possible characters. It can also handle more complicated wildcards than ?, as long as subtrees can be efficiently folded together. However, it does require the full tree of strings to be stored in memory, limiting its applicability, unless some truly cursed sparse segtree magic happens...
That's about all for this weird little technique. I hadn't heard of it before, and neither had Jasonwei08, who seems to know every technique in existence, idk. So, I hope you enjoyed this, and maybe someday the perfect problem will come up where it can be used!










