| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
Для каждой буквы будем поддерживать суммарную длину слов (cnt1ci), в которых встречается она одна, а для каждой пары букв будем поддерживать суммарную длину слов, в которых встречаются только они(cnt2ci, cj).
Для каждой строки определим количество различных букв в ней. Если она одна, то добавим к этой букве длину этого слова. Если их две, то добавим к этой паре букв длину этого слова.
Переберем пару букв, которая будет ответом. Для пары букв ci, cj ответом будет cnt1ci + cnt1cj + cnt2ci, cj. Среди всех таких пар найдем максимум и выведем его.
Решение за O(суммарная длина всех строк + 26 * 26)
Заметим, что если i-я прямая пересекаются с j-й в данной полосе, а при x = x1 i-я прямая находится выше, то при x = x2 выше окажется j-я прямая.
То есть отсортируем прямые по координате y при x = x1 + eps, и при x = x2 - eps. Проверим, что порядок прямых в обоих случаях совпадает. Если существует такая прямая, что ее индекс в первом случае не совпадает со вторым, то выведем Yes. В другом случае выведем No.
Единственное, что может нам помешать это пересечение на границах, так как в таком случае порядок сортировки не определен. Тогда прибавим к нашей границе x1 бесконечно малую величину eps, а от x2 отнимем eps, и порядок сортировки будет задан однозначно.
Решение за O(nlogn)
Одним из ответов будет являться сумма таких выражений для каждой окружности по координате x и аналогично по координате y: 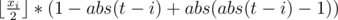
Пусть a = 1, b = abs(t - i), тогда это можно записать как 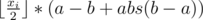
Рассмотрим a - b + abs(a - b):
если a ≤ b, то a - b + abs(a - b) = 0,
если a > b, то a - b + abs(a - b) = 2a - 2b
теперь рассмотрим, что такое a > b:
1 > abs(t - i)
i > t - 1, и i < t + 1.
При целом i это возможно лишь в случае i = t.
То есть эта скобка не обнуляется лишь при i = t.
Рассмотрим 2a - 2b = 2 - 2 * abs(t - i) = 2. Тогда 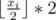 отличается от нужной координаты не более чем на 1, но так как все радиусы не меньше 2, то эта точка принадлежит окружности.
отличается от нужной координаты не более чем на 1, но так как все радиусы не меньше 2, то эта точка принадлежит окружности.
Решение за O(n).
Рассмотрим задачу без запросов второго типа. Заметим, что в графе, где все числа на ребрах > 1 максимальное количество присвоений 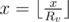 до того, как x превратится в 0, не превышает 64. Действительно, если все Rv = 2, то количество операций можно оценить как log2(x). Подвесим дерево за какую-нибудь вершину и назовем ее корнем.
до того, как x превратится в 0, не превышает 64. Действительно, если все Rv = 2, то количество операций можно оценить как log2(x). Подвесим дерево за какую-нибудь вершину и назовем ее корнем.
Научимся решать задачу при условии, что для любого v Rv > 1 и нет запросов второго типа. Для каждой вершины кроме корня мы определили ее предка как соседа наиболее близкого к корню. Пусть у нас был запрос первого типа от вершины a до вершины b с иходным числом x. Разобьем путь на две вертикальные части, одна из которых приближается к корню, а другая отдаляется. Найдем все ребра на этом пути. Для этого посчитаем глубину каждой вершины как расстояние до корня. Теперь будем параллельно подниматься в дереве из обеих вершин, пока не встретимся в общей. Если в ходе такого подъема мы прошли более 64 ребер, то в ходе замен 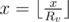 мы получим x = 0 и мы можем на текущем шаге остановить алгоритм поиска. Таким образом, мы совершим не более O(log(x)) операций.
мы получим x = 0 и мы можем на текущем шаге остановить алгоритм поиска. Таким образом, мы совершим не более O(log(x)) операций.
Перейдем к задаче, где Rv > 0. Заметим, что наше предыдущее решение в таком случае может работать за O(n). Так как при прохождении по ребру с Rv = 1 наше значение не меняется. Сведем эту задачу к выше рассмотренной. Сожмем граф, то есть уберем все единичные ребра. Для этого запустим dfs от корня и будем хранить самое глубокое ребро на пути от корня до вершины с Rv > 1.
Вспомним, что у нас были запросы уменьшения Rv. Будем поддерживать ближайшего предка Pv c RPv > 1. Воспользуемся идеей сжатия путей. При ответе на запрос первого типа будем пересчитывать Pv. Введем рекурсивную функцию F(v). Которая возвращает v, если Rv > 1, иначе выполняет присвоение Pv = F(Pv) и возвращает F(Pv). Каждое ребро мы удалим 1 раз, значит суммарно вызов всех функций F(v) работает O(n).
Итоговое время работы O(logx) на запрос первого типа и O(1) в среднем на запрос второго типа.
Научимся решать задачу для маленьких t. Воспользуемся стандартной динамикой dpx, y, t = количеству способов попасть в клетку (x; y) в момент времени t. Пересчет это сумма по всем допустимым способам попасть в клетку (x; y) в момент времени t – 1.
Заметим, что такую динамику можно считать при помощи возведения матрицы в степень. Заведем матрицу переходов, Ti, j = 1, если мы можем попасть из клетки i в клетку j. Пусть у нас был вектор G, где Gi равно количеству способов попасть в клетку i. Тогда новый вектор G' через dt секунд G' = G * (Tdt).
Таким образом мы научились решать задачу без изменений за O(log dt * S3), где dt — момент времени, S – площадь.
Рассмотрим, что происходит в момент добавления и удаления кота. При таких запросах изменяется матрица переходов. Между этими запросами T постоянная, значит мы можем возводить матрицу в степень. Таким образом, в момент изменения мы пересчитываем T, а между изменениями возводим матрицу в степень.
Решение за O(m * S3 log dt), m – количество запросов
Реализация
Для каждого города определим: за кого он голосует. Просуммируем для каждого кандидата и определим победителя.
O(n * m)
Математика, разбор случаев
Поймем, какие ходы интересные. Заметим, что Андрею нет смысла делать ход, при котором |a–m| > 1 так, как мы можем увеличить вероятность победы, если подвинем число a ближе к m.
Таким образом, мы рассматриваем два варианта хода a = c–1 и a = c + 1. Вероятность победы в первом случае c / n, во втором (n–c + 1) / n. Выбираем наилучший вариант. Нужно помнить про случай n = 1.
O(1)
Разбор случаев, (возможно) структуры
Рассмотрим, как происходят замены. Если был отрезок из точек длины l, то мы потратим l–1 операцию и прекратим замены для этого отрезка. Если просуммировать длины всех отрезков и их количества, то ответ это суммарная длина минус количество отрезков.
После изменения одного типа символа длина изменятся на 1. Количество отрезков можно поддерживать при помощи массива. Рассмотрим события слияния, деление, появление и удаление отрезков.
Для слияния смотрим на правого и левого соседа. Если они являются точками, то произошло слияние и количество отрезков уменьшилось на 1. Остальные случаи аналогично можно разобрать.
O(n + m)
DFS, бинарный поиск
Запишем вершины в порядке DFS от корня для вершин каждой глубины отдельно, храним время входа/выхода из вершины в DFS. Все вершины находящиеся в поддереве v, в такой записи представляют отрезок. Теперь мы умеем получать все вершины в v на высоте h, в виде отрезка, делая два бинарных поиска.
Палиндром можно составить, если количество нечетных вхождений каждой буквы меньше 2. Эту функцию можно посчитать для каждого префикса в обходе на каждой глубине отдельно.
Для экономии памяти можно воспользоваться битовым сжатием, поняв, что нас интересует только четность и функция – это xor.
O(m * (logn + 26) + n) – времени O(n * 26) — памяти, существует оффлайн решение за O(m * 26 / 32 + n) и O(n * 26 / 8) памяти
ДП
Нас интересуют пути являющиеся палиндромами. Палиндром читается с начала и с конца одинаково. Воспользуемся этим. Считаем динамику от координат двух клеток, первой и последней в палиндроме.
Из каждого состояние есть 4 перехода (комбинации: первая клетка вниз/вправо и вторая клетка вверх/влево). Нас интересуют переходы только по равным символам, по свойству палиндрома. Заметим, что нас интересуют пары клеток находящихся на одинаковом расстоянии от начала и конца соответственно. Если у первой клетки координаты (x1;y1), у последней (x2;y2), то x1 + y1 = n + m - x2 - y2.
Чтоб сэкономить память воспользуемся идеей хранить 2 последних слоя. O(n3) – времени и O(n2) — памяти
Доброго всем времени суток!
13 августа 2015 года в 19:30 MSK состоится очередной раунд Codeforces #316 для участников из второго дивизиона. Традиционно, участники из первого дивизиона могут участвовать в соревновании вне конкурса.
Это мой первый Codeforces раунд. Надеюсь, он вам понравится.
Хотелось бы сказать большое спасибо Максиму Ахмедову (Zlobober) за помощь в подготовке задач, Марии Беловой (Delinur) за перевод условий на английский, Михаилу Мирзаянову (MikeMirzayanov) за замечательные системы Codeforces и Polygon.
Участникам будет предложено пять задач и два часа на их решение.
UPD: Распределение баллов по задачам 500-1000-1500-2000-2500
Желаю всем участникам удачи!
UPD: Всем спасибо за участие!
Поздравляем победителей!
Дан массив натуральных чисел а ( MAX_A <= 105 ) длинны n ( n < = 30). Необходимо ответить для какого количества натуральных С невозможно подобрать набор t являющийся решением уравнения  , где ti целое число и ti >= 0. Гарантируется что ответ конечный.
, где ti целое число и ti >= 0. Гарантируется что ответ конечный.
Задан массив A и задаются запросы l r x. Ответ это 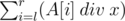 где div операция целочисленного деления. Хочется увидеть решение онлайн. Не могли бы вы подсказать как решается эта задача? UPD: Всем спасибо за ответ!
где div операция целочисленного деления. Хочется увидеть решение онлайн. Не могли бы вы подсказать как решается эта задача? UPD: Всем спасибо за ответ!
| Название |
|---|


