Hello Codeforces! (Long Post!)
Introduction
As I've recently solved my first ever $$$\ge$$$ 3000 rated problem (3300) on Codeforces — Codeforces Round #773 (Div. 1) Problem E — Special Positions and the solution that I came up with is different than the one presented in the official editorial, I thought that it will be valuable to the community if I share my approach.

Note that problem solving is a complicated & creative process. In the editorial, I show clean steps to reach the final solution, but the jump between each step is not always trivial (and sometimes hard!). Reaching this solution involved a large amount of drawings, observations, calculations & mistakes. There's no magic trick (at least to my knowledge :) ).
Alright, enough introduction, let's get started!
(click "The Editorial" below this line in order to be able to view the editorial)
From this point, I assume that you've at least read the problem, so if you haven't, click here in order to read the statement of the problem.
Note that in the editorial, I always use 0-based indexing.
We are given a non-empty subset $$$P$$$ of indexes and we wish to find the expected value of some scary expression dependent on $$$T$$$, where we randomly select $$$T$$$ out of all non-empty subsets of $$$P$$$ (with equal probability). Note that in this editorial, when I index $$$P$$$ or $$$T$$$, I refer to them as a sorted set. For instance, $$$P_0$$$ is the smallest element in $$$P$$$.
Recall the expression of interest: $$$\displaystyle\sum\limits_{i=0}^{n-1}{(a_i \cdot \min\limits_{j \in T}{|j-i|})}$$$ ( $$$a$$$ is the given array, $$$T$$$ is the chosen subset of indexes out of all non empty subsets of the given subset). This expression is essentially the sum of the multiplication of each element by some coefficient. When we talk about "the coefficient of an element", we refer to the value multiplied by the element in the summation.
For comfort reasons when making arguments, we'll solve a version of the problem where $$$T$$$ can also be empty, i.e a random subset of $$$P$$$ is selected with equal probability and if it's empty just say that the result value is 0. The reason this makes things more comfort, is that now the probability a certain element $$$i$$$ from $$$P$$$ is selected to be in $$$T$$$ is exactly $$$\frac{1}{2}$$$. this wasn't the case before, because of the empty set not being allowed. Further note that now, the probability of a state of $$$k$$$ elements of $$$p$$$ being a specific state (i.e, for each element of the $$$k$$$ elements, whether it's selected or not), is $$$\frac{1}{2^k}$$$.
We can recover the answer to the original problem using the fact that E[the expression] = E[the expression | T is not the empty set] * p(T is not empty), namely E[the expression | T is not the empty set] = E[the expression] / p(T is not empty).
Note: In the editorial, we sometimes make use of powers of $$$2$$$ or $$$\frac{1}{2}$$$ between the $$$0$$$th & the $$$m$$$th power. These can be calculated in $$$O(1)$$$, after pre-processing all of them in $$$O(m)$$$ and keeping them in some array.
Let the distance between two indexes to be the absolute value of their differences.
Notice that the coefficient of $$$a_i$$$ in the expression, is the distance of it's index to the closest index which is in $$$T$$$. Furthermore, observe that this index is either the closest index from the left, or the closest index from the right, namely, the biggest index in $$$T$$$ which is $$$< i$$$, or the smallest index in $$$T$$$ which is $$$> T$$$.
Initially when solving this problem, after making some observations on the structure of the problem, one could try to "solve the problem for each suffix" (you can arrive at attempting this by noticing that if you select some index $$$P_x$$$ to be in $$$T$$$, then the values of the coefficients of everything to the right of it are completely independent from everything to the left of $$$P_x$$$ being in $$$T$$$ or not, as such indexes are necessarily farther than everything to the right of $$$P_x$$$ than $$$P_x$$$ is).
Namely, you can sort of do something like letting $$$f(j)$$$ be the answer to the problem where $$$P_j$$$ is given to be in $$$T$$$ and the array the sum is calculated over is $$$a_{P_j} .. a_{n-1}$$$ (i.e, the "world" of the problem is only the suffix starting from $$$P_j$$$). Note that the answer to the whole problem can be expressed as summing for each element of $$$P$$$, the probability that it's the first index chosen to be in $$$T$$$ (i.e all the indexes in P smaller than it are not chosen to be in $$$T$$$), multiplied by the expected value given so, which is exactly $$$f(j)$$$ + the cost of the prefix up to the first chosen index. The probability that $$$P_i$$$ will be the first element is $$$\frac{1}{2^{i+1}}$$$, so the answer to the full problem is $$$\displaystyle\sum\limits_{i=0}^{m-1}{(\frac{1}{2^{i+1}} \cdot (f(i) + \text{cost of the prefix} 0..P_{i} \text{, where only} P_{i} \text{is selected})})$$$, and the cost of the prefix is $$$\displaystyle\sum\limits_{j=0}^{P_i}{(P_i-j) \cdot a_j}$$$. So, how do we calculate $$$f(j)$$$? Suppose the first index chosen after $$$P_j$$$ is $$$P_k$$$ ($$$P_{j+1}$$$ .. $$$P_{k-1}$$$ are all not chosen). The probability of this happening is $$$\frac{1}{2^{k-j}}$$$, and given this, the expected value of everything to the left of $$$P_k$$$ is exactly $$$f(k)$$$! Note that with probabiliy $$$\frac{1}{2^{m-1-j}}$$$ nothing is chosen, and in this case the value is easy to calculate. Before talking about an expression for f(j), let's introduce some helper functions.
Suppose index $$$i$$$ is chosen, then the next index chosen after it in the array is index $$$j$$$ (no other index is chosen in the middle), then the "value" of this part of the array is independent from indexes $$$< i$$$ or $$$> j$$$ being in $$$T$$$ or not, and is precisely equal to $$$0 \cdot a_i + 1 \cdot a_{i+1} + 2 \cdot a_{i+2} + .. + \lfloor \frac{i+j}{2} \rfloor \cdot a_{\lfloor \frac{i+j}{2} \rfloor} + .. + 2 \cdot a_{j-2} + 1 \cdot a_{j-1} + 0 \cdot a_{j}$$$. The value goes up by 1 each time you "step" forward in the region where $$$i$$$ is closer to the index than $$$j$$$, and the same logic for the other side. Formally, this is due to the coefficient of $$$a_k$$$ where $$$i \le k \le j$$$ being $$$min(k-i, j-k)$$$ and the way this function behaves. Let $$$cost(i,j)$$$ be this value. let $$$pcost(i)$$$ be the "value" of the prefix $$$[0,i]$$$ where only $$$i$$$ is in $$$T$$$. Similarly, let $$$scost(i)$$$ be the "value" of the suffix $$$[i,n-1]$$$ where only $$$i$$$ is in $$$T$$$. The formulas for $$$pcost$$$ and $$$scost$$$ are simply for each element, it's value multiplied by the distance from i.
To summarize: $$$cost(i,j) = \displaystyle\sum\limits_{k=i}^{j}{min(k-i, j-k) \cdot a_i}$$$
$$$pcost(i) = \displaystyle\sum\limits_{k=0}^{i}{(i-k) \cdot a_i}$$$
$$$scost(i) = \displaystyle\sum\limits_{k=i}^{n-1}{(k-i) \cdot a_i}$$$
By utilizing all of our observations & these helper functions, we can now write a clean formula for $$$f(j)$$$:
$$$f(j) = \displaystyle\sum\limits_{k=j+1}^{m-1}{(\frac{1}{2^{k-j}} \cdot (cost(P_j,P_k) + f(k)))} + \frac{1}{2^{k-j}} \cdot scost(P_j)$$$

Calculate all the $$$f$$$ values in decreasing order, and without any extra work we now have an $$$O(m^2 \cdot n)$$$ solution. We need to do much better.
Claim: with $$$O(n)$$$ of preprocessing, $$$cost$$$, $$$pcost$$$ & $$$scost$$$ can be calculated in $$$O(1)$$$.
How? prefix sums! (a bunch of them)
As mentioned before, the coefficients of the elements in $$$cost$$$, have an increasing part $ a decreasing part.
Let $$$inc(l,r) = \displaystyle\sum\limits_{i=l}^{r}{((i-l) \cdot a_i)}$$$ (each element multiplied by it's distance from the left (first by 0, second by 1, ...)
Let $$$dec(l,r) = \displaystyle\sum\limits_{i=l}^{r}{((r-i) \cdot a_i)}$$$ (each element multiplied by it's distance from the right (last by 0, one before last by 1, ...)
For comfort reasons, if $$$r > l$$$, or if at least one of them isn't a valid index, let $$$inc$$$ & $$$dec$$$ both be 0.
Observe that based on the way we analyzed $$$cost$$$ before, $$$cost(l,r) = inc(l, \lfloor \frac{l+r}{2} \rfloor) + dec(\lfloor \frac{l+r}{2} \rfloor + 1, r)$$$
Let's find a way to use some prefix sums for a fast calculation of $$$inc$$$ & $$$dec$$$
Let $$$g(i)$$$ be the sum of the first $$$i+1$$$ elements. Notice that $$$g(0) = 0$$$, $$$g(i) = a_i + g(i-1)$$$ for $$$i > 0$$$.
Let $$$g_{u}(i)$$$ be the summation of each of the first $$$i+1$$$ elements multiplied by its index. Notice that $$$g_{u}(0) = 0$$$, $$$g_{u}(i) = i \cdot a_i + g_{u}(i-1)$$$ for $$$i > 0$$$
Let $$$g_{d}(i)$$$ be the summation of each element in the suffix $$$[i, n-1]$$$ multiplied by n — 1 — its index. Notice that $$$g_{d}(n-1) = 0$$$, $$$g_{d}(i) = (n - 1 - i) \cdot a_i + g_{d}(i+1)$$$ for $$$i < n - 1$$$
Each of these function's values over all indexes can be pre-processed by using their recurrence relations.
For comfort reasons, define the value of each of these functions for numbers which are not a valid index to be $$$0$$$.
let $$$sum(l, r)$$$ be the sum of the elements in the subarray $$$a_l .. a_r$$$. Notice that $$$sum(l, r) = g(r) - g(l-1)$$$.
Claim: $$$inc(l, r) = g_{u}(r) - g_{u}(l-1) - l \cdot sum(l, r)$$$, $$$dec(l, r) = g_{d}(l) - g_{d}(r+1) - (n - 1 - r) \cdot sum(l, r)$$$. You can see why these claims are true visually, or quickly proof formally by playing with the summation expressions.
Substituting into the $$$cost$$$ formula: $$$cost(l, r) = g_{u}(\lfloor \frac{l+r}{2} \rfloor) - g_{u}(l-1) - l \cdot sum(l, \lfloor \frac{l+r}{2} \rfloor) + g_{d}(\lfloor \frac{l+r}{2} \rfloor + 1) - g_{d}(r+1) - (n - 1 - r) \cdot sum(\lfloor \frac{l+r}{2} \rfloor + 1, r)$$$
$$$cost(l, r) = g_{u}(\lfloor \frac{l+r}{2} \rfloor) - g_{u}(l-1) - l \cdot (g(\lfloor \frac{l+r}{2} \rfloor) - g(l-1)) + g_{d}(\lfloor \frac{l+r}{2} \rfloor + 1) - g_{d}(r+1) - (n - 1 - r) \cdot (g(r) - g(\lfloor \frac{l+r}{2} \rfloor))$$$

Note that with similar logic: $$$pcost(i) = dec(0, i)$$$, $$$scost(i) = inc(i, n-1)$$$
So now $$$f(j)$$$ is calculatable in $$$O(m)$$$ (as we can calculate $$$scost$$$ & $$$cost$$$ in $$$O(1)$$$ after $$$O(n)$$$ preprocessing), so our new best complexity is $$$O(m^2 + n)$$$. This is still not good enough.
So at this point one can continue with the $$$f(j)$$$ idea, and perhaps maintain some weighted sums of terms dependent on $$$l$$$ and terms dependent on $$$r$$$, but $$$f(k)$$$ & the terms dependent on $$$\lfloor \frac{l+r}{2} \rfloor$$$ make it hard.
We need to look at the problem from a new perspective.
for a specific subset $$$T$$$ being chosen, if we think about it, we gain some combination of $$$cost$$$ values, a $$$pcost$$$ value & a $$$scost$$$ value. Specifcally, we get $$$pcost$$$ of the smallest index chosen, $$$scost$$$ of the largest index chosen, and $$$cost$$$ values for all consecutive pairs in T (if we look at T as a sorted list of indexes).
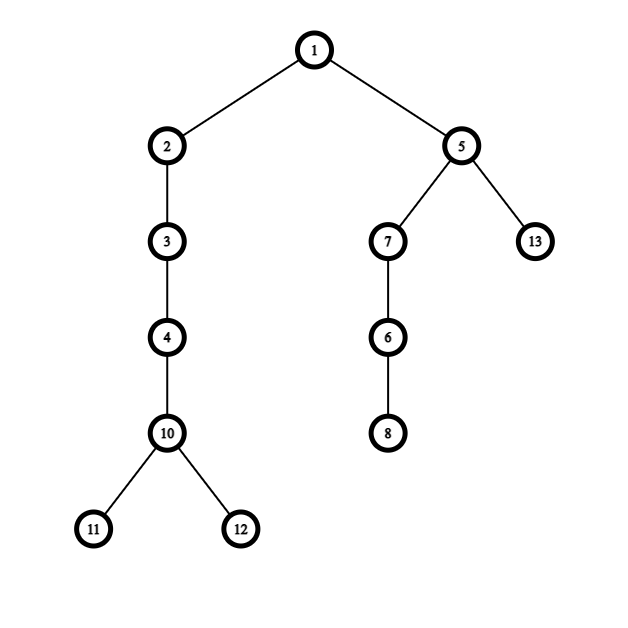
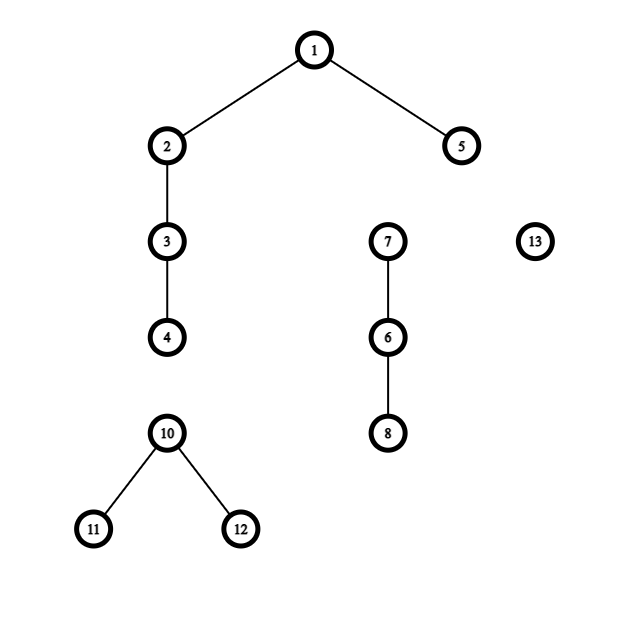
For example: — — — — X — — — — X — — — — X — — X — — —
(X represents a selected spot)
In this example, we gain $$$pcost(4)$$$, $$$cost(4, 9)$$$, $$$cost(9, 14)$$$, $$$cost(14, 17)$$$, $$$scost(17)$$$
The idea is that the expected value of the expression should be equal to the sum for each pcost/cost/scost value, the value * the probability it's "block" appears in a picture like the picture in the above example.
Let's introduce this idea more formally by using linearity of expectation.
Note: I'm being extra formal, I suggest you simply take a pen & some paper, and draw to understand the above claim. What essentially try to show formally in the explanation below is expressing the expected value as the sum of "expected values" of each "block" (cost/pcost/scost) (the value of a "block" is 0 if it doesn't appear, or its value if it does).
Let $$$C_{i,j}(T)$$$ be $$$cost(P_i,P_j)$$$ if $$$P_i$$$ & $$$P_j$$$ are in $$$T$$$ and no index in between them is in $$$T$$$, or $$$0$$$ otherwise
Let $$$PC_i(T)$$$ be $$$pcost(P_i)$$$ if $$$P_i$$$ is the smallest index in $$$T$$$, or $$$0$$$ otherwise.
Let $$$SC_i(T)$$$ be $$$scost(P_i)$$$ if $$$P_i$$$ is the largest index in $$$T$$$, or $$$0$$$ otherwise.
The expression we desire to find the expected value of can simply expressed as the sum of all of these variables, because each variable represents a unique "block", and is 0 if that block doesn't appear in the picture above, so only the values of relevant blocks will be considered.
So $$$\displaystyle\sum\limits_{i=0}^{n-1}{(a_i \cdot \min\limits_{j \in T}{|j-i|})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(C_{i,j}(T))})} + \displaystyle\sum\limits_{i=0}^{m-1}{(PC_i(T) + SC_i(T))}$$$
Apply linearity of expectation:
$$$\mathbb{E}[\text{the expression}] = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\mathbb{E}[C_{i,j}])})} + \displaystyle\sum\limits_{i=0}^{m-1}{(\mathbb{E}[PC_i] + \mathbb{E}[SC_i])}$$$
the probability of $$$C_{i,j}$$$ being "active" (the block appears), is $$$\frac{1}{2^{j-i+1}}$$$ (we essentially ask what's the probability for a certain fixed state of $$$j-i+1$$$ elements in $$$P$$$ (the elements which are within the block's region)).
Therefore, $$$\mathbb{E}[C_{i,j}] = \frac{1}{2^{j-i+1}} \cdot cost(P_i, P_j)$$$.
By applying similar logic: $$$\mathbb{E}[PC_i] = \frac{1}{2^{i+1}} \cdot pcost(P_i)$$$, $$$\mathbb{E}[SC_i] = \frac{1}{2^{m-1-i+1}} \cdot scost(P_i)$$$
Substituting the results:
$$$\mathbb{E}[\text{the expression}] = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{j-i+1}} \cdot cost(P_i, P_j))})} + \displaystyle\sum\limits_{i=0}^{m-1}{(\frac{1}{2^{i+1}} \cdot pcost(P_i) + \frac{1}{2^{m-1-i+1}} \cdot scost(P_i))}$$$
As we have $$$O(1)$$$ expressions for $$$cost$$$, $$$pcost$$$ & $$$scost$$$ (after preprocessing in $$$O(n)$$$), this can be calculated in $$$O(m^2)$$$. So, we have a different $$$O(m^2 + n)$$$ solution.

We can calculate the $$$\displaystyle\sum\limits_{i=0}^{m-1}{(\frac{1}{2^{i+1}} \cdot pcost(P_i) + \frac{1}{2^{m-1-i+1}} \cdot scost(P_i))}$$$ in $$$O(n)$$$, so the main challenge is to calculate $$$\displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{j-i+1}} \cdot cost(P_i, P_j))})}$$$ fast.
Recall the $$$cost$$$ formula we found:
$$$cost(l, r) = g_{u}(\lfloor \frac{l+r}{2} \rfloor) - g_{u}(l-1) - l \cdot (g(\lfloor \frac{l+r}{2} \rfloor) - g(l-1)) + g_{d}(\lfloor \frac{l+r}{2} \rfloor + 1) - g_{d}(r+1) - (n - 1 - r) \cdot (g(r) - g(\lfloor \frac{l+r}{2} \rfloor))$$$
let's group together terms that depend on the same thing:
$$$cost(l, r) = - g_{u}(l-1) + l \cdot g(l-1) - g_{d}(r+1) - (n - 1 - r) \cdot g(r) + g_{u}(\lfloor \frac{l+r}{2} \rfloor) + g_{d}(\lfloor \frac{l+r}{2} \rfloor + 1) + (n - 1 - (r + l)) \cdot g(\lfloor \frac{l+r}{2} \rfloor)$$$
Let $$$A(x) = - g_{u}(x-1) + x \cdot g(x-1)$$$
Let $$$B(x) = - g_{d}(x+1) - (n - 1 - x) \cdot g(x)$$$
Let $$$W(x) = g_{u}(\lfloor \frac{x}{2} \rfloor) + g_{d}(\lfloor \frac{x}{2} \rfloor + 1) + (n - 1 - x) \cdot g(\lfloor \frac{x}{2} \rfloor)$$$
Then $$$cost(l,r) = A(l) + B(r) + W(l+r)$$$
This expression seems much more friendly! Note that $$$A(x)$$$, $$$B(x)$$$ & $$$W(x)$$$ values for all valid $$$x$$$ can be pre-processed in $$$O(n)$$$ (they all depend on functions which we have shown that can be pre-processed in $$$O(n)$$$)
Substituting in the value that we are still looking for: $$$\displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{j-i+1}} \cdot cost(P_i, P_j))})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{A(P_i) + B(P_j) + W(P_i+P_j)}{2^{j-i+1}})})}$$$
Let $$$S_A = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{A(P_i)}{2^{j-i+1}})})}$$$
Let $$$S_B = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{B(P_j)}{2^{j-i+1}})})}$$$
Let $$$S_W = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{W(P_i+P_j)}{2^{j-i+1}})})}$$$
So, the value we are still looking for is exactly $$$S_A + S_B + S_W$$$. If we are able to calculate the value of each of the 3 terms fast, we win.
Let's begin with $$$S_A$$$.
$$$S_A = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{A(P_i)}{2^{j-i+1}})})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\frac{A(P_i)}{2^{-i+1}} \cdot \displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^j})})}$$$
Let's calculate the values summed over all $$$i$$$ from $$$i=m-1$$$ to $$$i=0$$$. During the calculation of the terms, we'll maintain a helper variable $$$H_1 = \displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^j})}$$$, which is the value we need to multiply $$$\frac{A(P_i)}{2^{-i+1}}$$$ by.
At first, before iterating over the $$$i$$$ values, set $$$H_1 = 0$$$, $$$S_A = 0$$$. When we are at some $$$i$$$, add to $$$S_A$$$ $$$\frac{A(P_i)}{2^{-i+1}} \cdot H_1$$$. Then, add $$$\frac{1}{2^i}$$$ to $$$H_1$$$, to be used in the next iterations.
If you are uncomfortable with this approach, you can also pre-process $$$H_1(i) = \displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^j})}$$$ like a DP (like pre-processing array prefix/suffix sums), then use them to calculate $$$S_A$$$ without maintating an extra helper variable during the calculation.
To summarize, we have demonstrated a way to calculate $$$S_A$$$ in $$$O(m+n)$$$ (the $$$+n$$$ part is due to preprocessing $$$A(x)$$$ values)..
One down, two left.
Let's tackle $$$S_B$$$.
$$$S_B = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{B(P_j)}{2^{j-i+1}})})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\frac{1}{2^{-i+1}} \cdot \displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{B(P_j)}{2^{j}})})}$$$
We can use exactly the same kind of trick. Let $$$H_2(i) = \displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{B(P_j)}{2^{j}})}$$$ (the part which is multiplied by $$$\frac{1}{2^{-i+1}}$$$.
We can either maintain $$$H_2$$$ as a helper variable, iterate over the indexes backwards and add it multiplied by $$$\frac{1}{2^{-i+1}}$$$ to the result, or calculate it like a DP backwards (like prefix/suffix sums) then calculate $$$S_B$$$ with $$$O(1)$$$ per term.
2/3 done, now for the hardest one — $$$S_W$$$.
Our trick won't work this time, we need to think harder.
$$$S_W = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{W(P_i+P_j)}{2^{j-i+1}})})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{-i+1}} \cdot \frac{1}{2^{j}} \cdot W(P_i+P_j))})}$$$.
This expression feels like polynomial multiplication!

Well, almost.
If we have a polynomial $$$U(x)$$$ of degree $$$u$$$, where the coefficient of $$$x^i$$$ is $$$s_i$$$ and a polynomial $$$V$$$ of degree $$$v$$$, where the coefficient of $$$x^i$$$ is $$$t_i$$$, then:
$$$U(x) = \displaystyle\sum\limits_{i=0}^{u}{(s_i \cdot x^{i})}$$$
$$$V(x) = \displaystyle\sum\limits_{i=0}^{v}{(t_i \cdot x^{i})}$$$
$$$U(x) \cdot V(x) = \displaystyle\sum\limits_{i=0}^{u}{(\displaystyle\sum\limits_{j=0}^{v}{(s_i \cdot x^{i} \cdot t_j \cdot x^{j})})} = \displaystyle\sum\limits_{i=0}^{u}{(\displaystyle\sum\limits_{j=0}^{v}{(s_i \cdot t_j \cdot x^{i+j})})}$$$
So, $$$U(x) \cdot V(x) = \displaystyle\sum\limits_{0 \le i \le u, 0 \le j \le v}{(s_i \cdot t_j \cdot x^{i+j})}$$$
Two polynomials can be multiplied in $$$O((u+v) \cdot log(u+v))$$$ via Fast Forier Transformation // Number-Theory-Transformation Important Note: you do NOT need to understand how FFT/NTT works internally in order to understand this editorial. Just suppose you have a black box which can multiply two polynomials in the specified complexity.
Recall that $$$S_W = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{-i+1}} \cdot \frac{1}{2^{j}} \cdot W(P_i+P_j))})}$$$.
First, let's convert the problem into a problem of finding a polynomial. Let's replace $$$W(P_i + P_j)$$$ with $$$x^{P_i+P_j}$$$, namely, let's define a polynomial $$$G(x) = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{-i+1}} \cdot \frac{1}{2^{j}} \cdot x^{P_i+P_j})})}$$$. Let $$$g_i$$$ be the coefficient of $$$x^i$$$ in $$$G$$$. Now, notice that $$$S_W = \displaystyle\sum\limits_{i=0}^{2 \cdot n - 2}{(g_i \cdot W(i))}$$$, because $$$g_i$$$ is exactly the sum of all terms multiplied by $$$x^i$$$, which is exactly the sum of all terms multiplied by $$$W(i)$$$ in $$$S_W$$$.
So, if we find fast the coefficients of the polynomial $$$G(x)$$$, we win.
If $$$x^{P_i+P_j}$$$ "gains" $$$\frac{1}{2^{-i+1}} \cdot \frac{1}{2^{j}}$$$, this gives us the motivation to define two polynomials, one with $$$\frac{1}{2^{-i+1}}$$$ as a coefficient of $$$x^{P_i}$$$ for all $$$i$$$, and one with $$$\frac{1}{2^{j}}$$$ as a coefficient of $$$x^{P_j}$$$ for all $$$j$$$. Formally:
Let $$$Y(i) = \displaystyle\sum\limits_{i=0}^{n-1}{y_i \cdot x^i}$$$, where $$$y_{P_i} = \frac{1}{2^{-P_i+1}}$$$ for all $$$i$$$, and the rest of the $$$y$$$ values are 0.
Let $$$K(i) = \displaystyle\sum\limits_{i=0}^{n-1}{k_i \cdot x^i}$$$, where $$$k_{P_i} = \frac{1}{2^{P_i}}$$$ for all $$$i$$$, and the rest of the $$$k$$$ values are 0.
Notice that $$$G(x) = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(\frac{1}{2^{-i+1}} \cdot \frac{1}{2^{j}} \cdot x^{P_i+P_j})})} = \displaystyle\sum\limits_{i=0}^{m-1}{(\displaystyle\sum\limits_{j=i+1}^{m-1}{(y_i \cdot k_i \cdot x^{P_i+P_j})})} = \displaystyle\sum\limits_{0 \le i < j \le n - 1}{(y_i \cdot k_i \cdot x^{P_i+P_j})}$$$
$$$Y(i) \cdot K(i) = \displaystyle\sum\limits_{0 \le i,j \le n-1}{(y_i \cdot k_i \cdot x^{i+j})}$$$
So, simply multiplying $$$Y(x)$$$ & $$$K(x)$$$ gives us exactly the expression we need, but with $$$0 \le i,j \le n-1$$$ instead of $$$0 \le i < j \le n-1$$$.
A vague informal idea is that if we multiply all elements from the "first half" of $$$Y$$$ with all elements from the "second half$ of $$$K$$$, then all of the pairs we get contributing to the coefficients of the resultant polynomial $$$G$$$ are pairs we need (as everything in the "second half" of $$$K$$$ has strictly larger $$$x$$$ powers than everything in the "first half" of $$$Y$$$ and we look for pairs where $$$i < j$$$), then we need to recursively calculate the contribution of elements from the "first" half of $$$Y$$$ combined with elements from the "first half" of $$$K$$$, and elements from the "second half" of $$$Y$$$ combined with elements from the "second half" of $$$K$$$ (and obviously, the contribution of elements from the "second half" of $$$Y$$$ combined with elements from the "first half" of $$$K$$$ is 0, (as everything in the "second half" of $$$Y$$$ has strictly larger $$$x$$$ powers than everything in the "first half" of $$$K$$$, and we look for pairs where $$$i < j$$$))
Namely, we want a divide & conquer algorithm.

Define the first-half-polynomial of a of a polynomial of degree $$$d$$$, say, $$$Z(x)$$$, where $$$z_i$$$ is the coefficient of $$$x^i$$$, to be $$$Z_0 = \displaystyle\sum\limits_{i=0}^{\lfloor \frac{d}{2} \rfloor}{(z_i \cdot x^i)}$$$.
Define the second-half-polynomial of a of a polynomial of degree $$$d$$$, say, $$$Z(x)$$$, where $$$z_i$$$ is the coefficient of $$$x^i$$$, to be $$$Z_1 = \displaystyle\sum\limits_{i=\lfloor \frac{d}{2} \rfloor+1}^{d}{(z_i \cdot x^i )}$$$.
Let $$$U(x), V(x)$$$ both be polynomial of degree $$$d$$$, where the coefficients of $$$U(x) $$$ are $$$s_i$$$, and the coefficients of $$$V(x)$$$ are $$$t_i$$$. define $$$U(x) \oplus V(x) = \displaystyle\sum\limits_{0 \le i < j \le d}{(s_i \cdot t_i \cdot x^{i+j})}$$$.
Note that based on this definition, $$$G(x) = Y(x) \oplus K(x)$$$.
Claim: Let $$$U(x), V(x)$$$ be polynomials defined exactly like before. for $$$d \ge 1$$$, $$$U(x) \oplus V(x) = U_0(x) \cdot V_1(x) + U_0(x) \oplus V_0(x) + U_1(x) \oplus V_1(x)$$$. This claim is true because for all valid pairs $$$i, j$$$, namely, pairs where $$$i < j$$$, either $$$x^i$$$ is in $$$U_0$$$ & $$$x^j$$$ is in $$$V_1$$$, and these values we gain by multiplying regularly $$$U_0$$$ & $$$V_1$$$, or $$$x^i$$$ is in $$$U_0$$$ & $$$x^j$$$ is in $$$V_0$$$, in which case we can use the same function we use the calculate $$$U(x) \oplus V(x)$$$ recursively, or $$$x^i$$$ is in $$$U_1$$$ & $$$x^j$$$ is in $$$V_1$$$, in which case we can (again) use the same function we use the calculate $$$U(x) \oplus V(x)$$$ recursively. Note that the only other option we did not mention is $$$x^i$$$ being in $$$U_1$$$ & $$$x^j$$$ being in $$$V_0$$$, but this option is impossible, as this imples $$$i > j$$$.
multiplying $$$U_0$$$ with $$$V_1$$$ takes $$$O(d \cdot \log(d))$$$ (as mentioned before, by using FFT/NTT). we recurse the job twice. once with $$$U_0$$$ & $$$V_0$$$, which are polynomials of degree $$$\lfloor \frac{d}{2} \rfloor$$$, and once with $$$U_1$$$ & $$$V_1$$$, which are polynomials of degree.. $$$d$$$? This is clearly bad, but the coefficients of their first $$$\lfloor \frac{d}{2} \rfloor + 1$$$ $$$x$$$ powers are 0! so instead of recursiving with $$$U_1(x)$$$ & $$$V_1(x)$$$, we can recurse with $$$\frac{U_1(x)}{x^{\lfloor \frac{d}{2} \rfloor + 1}}$$$ and $$$\frac{V_1(x)}{x^{\lfloor \frac{d}{2} \rfloor + 1}}$$$, which are polynomials of degree $$$d - \lfloor \frac{d}{2} \rfloor - 1 \le \lfloor \frac{d}{2} \rfloor$$$, then multiply the result by $$$x^{2 \cdot \lfloor \frac{d}{2} \rfloor + 1}$$$ to undo the effect of the divisions.
With our improvement, for degree $$$d$$$, we do $$$O(d \cdot \log(d))$$$ & recurse twice with degree $$$\lfloor \frac{d}{2} \rfloor$$$, hence the total complexity for the operation (by standard divide-and-conquer analysis) is $$$O(d \cdot \log(d)^2)$$$
To summarise, we can find the coefficients of the polynomial $$$G(x)$$$ by calculating $$$Y(x) \oplus K(x)$$$ via the method that we've presented in $$$O(n \cdot \log(n)^2)$$$, and we can use them to calculate $$$S_W$$$, so we have (finally!) arrived at an algorithm to find the expected value we desire in $$$O(n \cdot \log(n)^2)$$$.
$$$\blacksquare$$$