73573306 Getting WA, help me please
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 146 |
The inclusion-exclusion principle can be expressed as follows:
To compute the size of a union of multiple sets, it is necessary to sum the sizes of these sets separately, and then subtract the sizes of all pairwise intersections of the sets, then add back the size of the intersections of triples of the sets, subtract the size of quadruples of the sets, and so on, up to the intersection of all sets. The above definition can be expressed mathematically as follows:
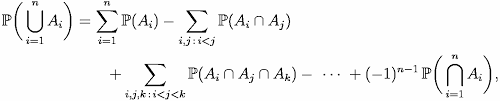
It is intuitive for $$$n\leq 3$$$. But I have some problem with it. I cannot understand why it is like that?! (previously thanks!)
It turns out, that the final amortized time complexity is $$$O(α(n))$$$, where $$$α(n)$$$ is the inverse Ackermann function, which grows very slowly. In fact it grows so slowly, that it doesn't exceed $$$4$$$ for all reasonable $$$n$$$ (approximately $$$n<10^{600})$$$.
int find_set(int v) {
if (v == parent[v])
return v;
return parent[v] = find_set(parent[v]);
}
Question: Why this works in $$$O(α(n))$$$?
Can someone explain me solution of the problem D?
Hello everyone, I'm a beginner at competetive programming, would anyone please suggest me some math/number theory problems for fast growth please? Because I'm really not so good at it and I'd like to develope (my Logic & Math), thanks in advance!
| Name |
|---|









