Hanoi Tower Troubles Again is a problem I recently discovered in "Programming Challenges" by Skiena and Revilla. It seems to be quite popular, because some (bad!) solutions can be found on various websites. I want to proof a nice explicit form here (see below).
It's trivial to solve this using (greedy) simulation (*). But Skiena and Revilla provide a short hint:
Can the constraints be usefully modeled using a DAG?
I thought about constructing a DAG where longest path corresponds to optimal solution. Unfortunately, my best approach is to use (a1, a2, ..., aN) as state where ai denotes number on ball on top of peg i; exponential number of vertices is bad. How to use this hint in a suitable way?
Considering small cases, one find the answers
1, 3, 7, 11, 17, 23, 31, 39, 49, 59, ...
for 1, 2, 3, ... pegs respectively. I conjecture that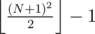 
is the answer in general.
Crawling through roughly a dozen websites with trivial simulation and no comments, I encountered a chinese article where a recurrence relation is given but not proven: h(1) = 1, h(2) = 3, h(i) = h(i - 1) + i for even i and h(i) = h(i - 1) + i + 1 for odd i.
Finally, there are two questions:
How to utilize a DAG suitable?
How to prove the recurrence and/or explicit form (if correct)?
Any kind of help and interesting ideas are appreciated!
(*) It's not immediately clear that solution is bounded and greedy simulation is correct.
