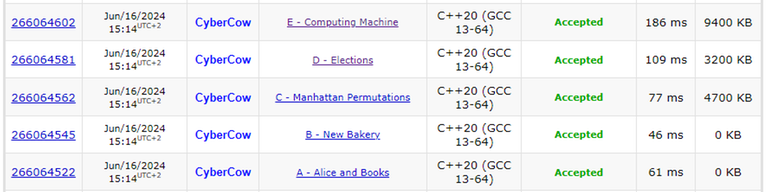
| A | B | C | D | E | F1 | F2 | |
|---|---|---|---|---|---|---|---|
| nifeshe | 800 | 1200 | 1400 | 2000 | 2200 | 2700 | 2800 |
| Intellegent | 800 | 1200 | 1600 | 2000 | 2300 | ||
| mwen | 800 | 1200 | 1300 | 1800 | 2300 | ||
| Markadiusz | 800 | 1100 | 1300 | 1800 | 2300 | 2500 | 2800 |
| _istil | 800 | [1600, 2000] | 2000 | 2400 | 2700 | ||
| hazzlek | 1000 | 1200 | 1500 | 2000 | 2100 | ||
| iLoveIOI | 800 | 1100 | 1600 | 2000 | 2400 | ||
| A_G | 800 | 1100 | 1500 | 1700 | 2100 | 2600 | 2700 |
| DilshodbekX | 800 | 1200 | 1500 | 1800 | 2200 |
| A | B | C | D | E | F1 | F2 | |
|---|---|---|---|---|---|---|---|
| Average | 822 | 1163 | 1500 | 1900 | 2238 | 2550 | 2750 |
| Actual | 800 | 1300 | 1200 | 2200 | 2500 | 2700 | 3000 |
Look at the picture. I mean, look at the picture.
Consider coordinates $$$x$$$ and $$$y$$$ separately.
Consider coordinates $$$x$$$ and $$$y$$$ separately. Since $$$1 \le x_i, y_i \le m - 1$$$, after each step both coordinates increase and remain connected with the previous square.
From the picture we can see that each coordinate spans from the bottom-left corner of the first square to the top-right corner of the last square.
To calculate the perimeter we can add the length of that interval for both coordinates and multiply it by $$$2$$$, as it is counted in the perimeter twice, going in both directions:
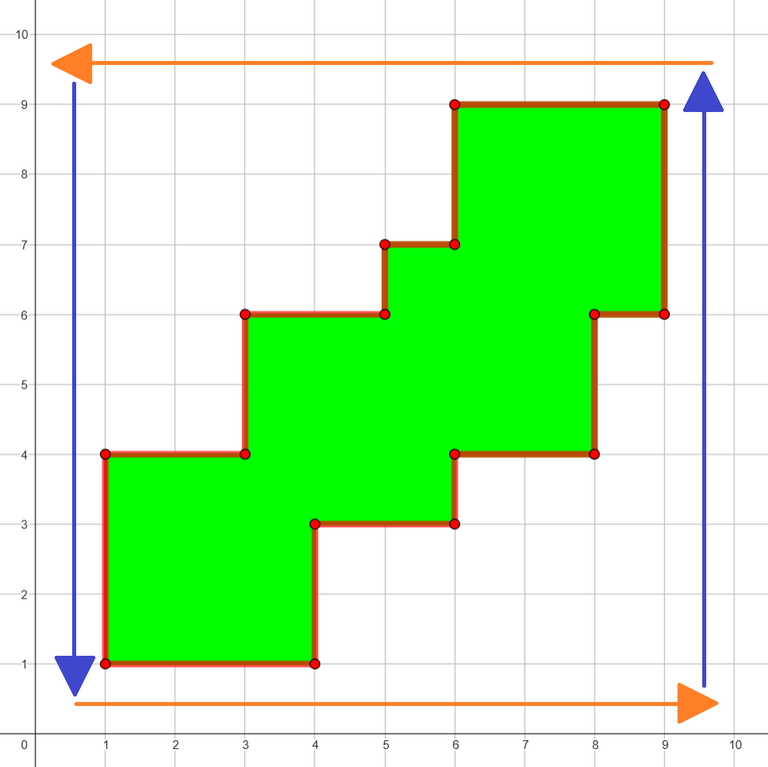
The coordinates of the bottom-left corner of the first square are $$$(x_1, y_1)$$$ and of the top-right corner of the last square are $$$(m + \sum\limits_{i = 1}^n x_i, m + \sum\limits_{i = 1}^n y_i)$$$.
The lengths of the intervals are $$$m + \sum\limits_{i = 2}^n x_i$$$ and $$$m + \sum\limits_{i = 2}^n y_i$$$.
Therefore, the answer is $$$2(2m + \sum\limits_{i = 2}^n (x_i + y_i))$$$.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n, m;
cin >> n >> m;
vector<int> x(n), y(n);
for(int i = 0; i < n; i++) {
cin >> x[i] >> y[i];
}
int ans = 2 * (accumulate(x.begin(), x.end(), 0) + m - x[0] + accumulate(y.begin(), y.end(), 0) + m - y[0]);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
"It can be proven that permutation $$$p$$$ can be uniquely determined"
This means that there is an order of elements. How to determine whether $$$x$$$ should be earlier in that order than $$$y$$$?
Consider two elements $$$x < y$$$. Suppose their positions in $$$p$$$ are $$$i$$$ and $$$j$$$ correspondigly.
How can we determine if $$$i < j$$$? If $$$i < j$$$ and $$$x < y$$$, we will have $$$g_{x, y} = g_{y, x} = 1$$$. Otherwise, $$$i > j$$$ and $$$x < y$$$, so $$$g_{x, y} = g_{y, x} = 0$$$.
So if $$$g_{x, y} = 1$$$, we know that $$$i < j$$$, otherwise $$$i > j$$$.
That way we can determine for each pair of elements which one of them should appear earlier in the permutation. Notice that this is just a definition of a comparator, which proves that the permutation is indeed unique. We can find it by sorting $$$p = [1, 2, \ldots, n]$$$ with that comparator.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
vector<string> g(n);
for(auto &i : g) {
cin >> i;
}
vector<int> p(n);
iota(p.begin(), p.end(), 0);
sort(p.begin(), p.end(),
[&](int x, int y) {
if(g[x][y] == '1') return x < y;
else return x > y;
});
for(auto i : p) cout << i + 1 << " "; cout << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
2056C - Palindromic Subsequences
Analyze the example with $$$n = 6$$$.
If $$$[a_1, a_2, \ldots, a_k, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is a palindrome, then $$$[a_1, a_2, \ldots, a_k, a_i, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is also a palindrome for all $$$k < i < n - k + 1$$$.
If $$$[a_1, a_2, \ldots, a_k, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is a palindrome, then $$$[a_1, a_2, \ldots, a_k, a_i, a_{n - k + 1}, a_{n - k + 2}, \ldots, a_n]$$$ is also a palindrome for all $$$k < i < n - k + 1$$$, because we make it's length odd and add $$$a_i$$$ to the middle.
We can use this to create a sequence with a big value of $$$g$$$. However, we shouldn't create a palindrome of a greater length than $$$2k + 1$$$ by using the fact above.
That make us try something like $$$a = [1, 2, 3, \ldots, n - 2, 1, 2]$$$. $$$f(a) = 3$$$ here, and any of $$$[a_1, a_i, a_{n - 1}]$$$ for $$$1 < i < n - 1$$$ and $$$[a_2, a_i, a_n]$$$ for $$$2 < i < n$$$ are palindromes, which means that $$$g(a) = 2(n - 3) = 2n - 6$$$.
This construction works for $$$n \ge 7$$$, so we have to handle $$$n = 6$$$ separately.
We can also use the construction from the example with $$$n = 6$$$ directly: $$$a = [1, 1, 2, 3, 4, \ldots, n - 3, 1, 2]$$$, which has $$$g(a) = 3n - 11$$$.
#include <bits/stdc++.h>
using namespace std;
void solve() {
int n;
cin >> n;
if (n == 6) {
cout << "1 1 2 3 1 2\n";
}
else if(n == 9) {
cout << "7 3 3 7 5 3 7 7 3\n";
}
else if(n == 15) {
cout << "15 8 8 8 15 5 8 1 15 5 8 15 15 15 8\n";
}
else {
for(int i = 1; i <= n - 2; i++) cout << i << " "; cout << "1 2\n";
}
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
Solve the problem when $$$a_i \le 2$$$.
Assign $$$b_i = 1$$$ if $$$a_i = 2$$$ and $$$b_i = -1$$$ if $$$a_i = 1$$$ and calculate the number of bad subarrays.
Extend this solution for $$$a_i \le 10$$$, however, you need to take overcounting into account.
When is a subarray $$$a[l, r]$$$ not good?
If $$$r - l + 1$$$ is odd, $$$a[l, r]$$$ can't be bad. Otherwise, suppose the median of $$$a[l, r]$$$ is $$$x$$$. Then there need to be exactly $$$\frac{r - l + 1}{2}$$$ elements in $$$a[l, r]$$$ that are $$$\le x$$$ and exactly $$$\frac{r - l + 1}{2}$$$ that are $$$> x$$$.
This gives us an idea to calculate the number of bad subarrays with a median of $$$x$$$.
Create another array $$$b$$$ of size $$$n$$$, where $$$b_i = -1$$$ if $$$a_i \le x$$$ and $$$b_i = 1$$$ otherwise.
$$$a[l, r]$$$, which has a median of $$$x$$$, is bad if and only if $$$\sum\limits_{i = l}^r b_i = 0$$$ and $$$r - l + 1$$$ is even.
Notice that the second condition is not needed, as the sum of an odd length subarray of $$$b$$$ is always odd, so it can't be zero.
Therefore, $$$a[l, r]$$$ with a median of $$$x$$$ is bad iff $$$\sum\limits_{i = l}^r b_i = 0$$$.
If there is no $$$x$$$ in $$$[l, r]$$$, then the median of $$$a[l, r]$$$ trivially can't be equal to $$$x$$$.
If there is an occurrence of $$$x$$$ in $$$a[l, r]$$$ and $$$\sum\limits_{i = l}^r b_i = 0$$$, notice that the median of $$$a[l, r]$$$ will always be exactly $$$x$$$. This is true because $$$\frac{r - l + 1}{2}$$$ smallest elements of $$$a[l, r]$$$ are all $$$\le x$$$, and there is an occurrence of $$$x$$$, so $$$\frac{r - l + 1}{2}$$$-th smallest element must be $$$x$$$.
This allows us to simply count the number of subarrays of $$$b$$$ with a sum of $$$0$$$ and with an occurrence of $$$x$$$ to count the number of bad subarrays with median $$$x$$$.
We can subtract that value from $$$\frac{n(n + 1)}{2}$$$ for all $$$x$$$ between $$$1$$$ and $$$A = 10$$$ to solve the problem in $$$O(nA)$$$.
#include <bits/stdc++.h>
using namespace std;
const int MAX = 11;
int main() {
int tests;
cin >> tests;
for(int test = 0; test < tests; test++) {
int n;
cin >> n;
vector<int> a(n);
for(auto &i : a) {
cin >> i;
}
long long ans = 0;
for(int x = 1; x < MAX; x++) {
vector<int> b(n);
for(int i = 0; i < n; i++) {
b[i] = (a[i] > x? 1 : -1);
}
int sum = n;
vector<int> pref(n);
for(int i = 0; i < n; i++) {
pref[i] = sum;
sum += b[i];
}
vector<int> cnt(2 * n + 1);
sum = n;
int j = 0;
for(int i = 0; i < n; i++) {
if(a[i] == x) {
while(j <= i) {
cnt[pref[j]]++;
j++;
}
}
sum += b[i];
ans += cnt[sum];
}
}
ans = 1ll * n * (n + 1) / 2 - ans;
cout << ans << '\n';
}
return 0;
}
Forget about counting. What is the maximum size of $$$T$$$ if $$$m = 0$$$?
It is $$$2n - 1$$$. What if $$$m$$$ isn't $$$0$$$?
It is still $$$2n - 1$$$. To prove this represent a good set as a forest.
We can always add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ to $$$S$$$. Now the tree of $$$S$$$ has exactly $$$n$$$ leaves. What if a vertex has more than $$$2$$$ children?
What is the number of solutions when $$$m = 0$$$?
It is the number of full binary trees with $$$n$$$ leaves, which is $$$C_{n - 1}$$$, where $$$C$$$ denotes the Catalan's sequence. Extend this idea to count the number of solutions for a general tree of $$$S$$$.
Any good set has a tree-like structure.
Specifically, represent $$$S$$$ as a forest the following way: segment $$$[l, r]$$$ has a parent $$$[L, R]$$$ iff $$$[l, r] \in [L, R]$$$ and $$$R - L + 1$$$ is minimized (its parent is the shortest interval in which it lies). This segment is unique (or does not exist), because there can't be two segments with minimum length that cover $$$[l, r]$$$, as they would partially intersect otherwise.
Notice that we can always add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ if they aren't in $$$S$$$ yet. Now the forest of $$$S$$$ is a tree with exactly $$$n$$$ leaves.
Suppose $$$[L, R]$$$ has $$$k$$$ children $$$[l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]$$$. If $$$k > 2$$$, we can always add $$$[l_1, r_2]$$$ to $$$S$$$, which decreases the number of children of $$$[L, R]$$$ by $$$1$$$ and increases the size of $$$S$$$ by $$$1$$$.
Therefore, in the optimal solution each segment has at most $$$2$$$ children. Having exactly one child is impossible, as we have added all $$$[i, i]$$$, so every index of $$$[L, R]$$$ is covered by its children.
This means that we have a tree where each vertex has either $$$0$$$ or $$$2$$$ children, which is a full binary tree.
We have $$$n$$$ leaves, and every full binary tree with $$$n$$$ leaves has exactly $$$2n - 1$$$ vertices, so this is always the optimal size of $$$T$$$ regardless of $$$S$$$.
To count the number of $$$T$$$, notice that when $$$m = 0$$$ the answer is the number of full binary trees with $$$n$$$ leaves, which is $$$C_{n - 1}$$$, where $$$C$$$ denotes the Catalan's sequence.
To extend this to a general tree, we can add $$$[1, n]$$$ and $$$[i, i]$$$ for all $$$1 \le i \le n$$$ to $$$S$$$.
Now suppose $$$[L, R]$$$ has $$$k \ge 2$$$ children $$$[l_1, r_1], [l_2, r_2], \ldots, [l_k, r_k]$$$. We need to merge some children. We can treat $$$[l_1, r_1]$$$ as $$$[1, 1]$$$, $$$[l_2, r_2]$$$ as $$$[2, 2]$$$, etc. This is now the same case as $$$m = 0$$$, so there are $$$C_{k - 1}$$$ ways to merge children of $$$[L, R]$$$.
Each vertex is independent of each other, so the answer is $$$\prod C_{c_v - 1}$$$ over all non-leaves $$$v$$$, where $$$c_v$$$ is the number of children of $$$v$$$.
We can construct the tree in $$$O(n \log n)$$$ by definition or in $$$O(n)$$$ using a stack.
#include <bits/stdc++.h>
using namespace std;
const int mod = 998244353;
const int MAX = 4e5 + 42;
int fact[MAX], inv[MAX], inv_fact[MAX];
int C(int n, int k) {
if(n < k || k < 0) return 0;
return (long long) fact[n] * inv_fact[k] % mod * inv_fact[n - k] % mod;
}
int Cat(int n) {
return (long long) C(2 * n, n) * inv[n + 1] % mod;
}
int binpow(int x, int n) {
int ans = 1;
while(n) {
if(n & 1) ans = (long long) ans * x % mod;
n >>= 1;
x = (long long) x * x % mod;
}
return ans;
}
void solve() {
int n, m;
cin >> n >> m;
int initial_m = m;
vector<pair<int, int>> a(m);
for(auto &[l, r] : a) {
cin >> l >> r;
}
bool was_full = 0;
vector<int> was_single(n + 1);
for(auto [l, r] : a) was_full |= (r - l + 1 == n);
for(auto [l, r] : a) {
if(l == r) was_single[l] = 1;
}
if(!was_full) {
a.push_back({1, n});
m++;
}
for(int i = 1; i <= n; i++) {
if(!was_single[i] && n != 1) {
a.push_back({i, i});
m++;
}
}
for(auto &[l, r] : a) r = -r;
sort(a.begin(), a.end());
vector<int> deg(m);
for(int i = 0; i < m; i++) {
int j = i + 1;
while(j < m) {
if(-a[i].second < a[j].first) break;
deg[i]++;
j = upper_bound(a.begin(), a.end(), make_pair(-a[j].second, 1)) - a.begin();
}
}
for(auto &[l, r] : a) r = -r;
int ans = 1;
for(int i = 0; i < m; i++) {
if(deg[i] > 0) {
assert(deg[i] >= 2);
ans = (long long) ans * Cat(deg[i] - 1) % mod;
}
}
cout << ans << '\n';
}
signed main() {
fact[0] = 1;
for(int i = 1; i < MAX; i++) fact[i] = (long long) fact[i - 1] * i % mod;
inv_fact[MAX - 1] = binpow(fact[MAX - 1], mod - 2);
for(int i = MAX - 1; i; i--) inv_fact[i - 1] = (long long) inv_fact[i] * i % mod;
assert(inv_fact[0] == 1);
for(int i = 1; i < MAX; i++) inv[i] = (long long) inv_fact[i] * fact[i - 1] % mod;
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
2056F1 - Xor of Median (Easy Version), 2056F2 - Xor of Median (Hard Version)
The order of the sequence doesn't matter. What if we fix the sequence $$$\text{cnt}$$$ and then calculate its contribution to the answer?
By Lucas's theorem the contribution is odd iff for each set bit in $$$n$$$ there is exactly one $$$i$$$ such that $$$\text{cnt}_i$$$ has this bit set, and $$$\sum\limits_{i = 0}^{m - 1} \text{cnt}_i = n$$$. In other words, $$$\text{cnt}$$$ has to partition all set bits in $$$n$$$. For a fixed $$$\text{cnt}$$$ with an odd contribution, what will be the median?
There is a very big element in $$$\text{cnt}$$$.
Since $$$\text{cnt}$$$ partitions the bits of $$$n$$$, there will be $$$i$$$ which has it's most significant bit. This means that $$$2\text{cnt}_i > n$$$, so $$$i$$$ will always be the median.
Suppose there are $$$p$$$ non-zero elements in $$$\text{cnt}$$$. We can partition all set bits of $$$n$$$ into $$$p$$$ non-empty subsequences and then choose which of the $$$m$$$ numbers will occur. How can we calculate the answer now?
The only time we use the value of $$$n$$$ is when we partition all of it's set bits into subsequences. That means that the answer only depends on the number of set bits in $$$n$$$, not on $$$n$$$ itself. This allows us to solve the easy version by fixing the value of $$$p$$$ and the value of the median.
To solve the hard version use Lucas's theorem again and do digit dp or SOS-dp.
The order of the sequence doesn't matter, so let's fix the sequence $$$\text{cnt}$$$ and calculate its contribution to the answer.
For a fixed $$$\text{cnt}$$$, the number of ways to order $$$a$$$ is $$$\binom{n}{\text{cnt}_0, \text{cnt}_1, \ldots, \text{cnt}_{m - 1}}$$$. By Lucas's theorem the contribution is odd iff for each set bit in $$$n$$$ there is exactly one $$$i$$$ such that $$$\text{cnt}_i$$$ has this bit set, and $$$\sum\limits_{i = 0}^{m - 1} \text{cnt}_i = n$$$. In other words, $$$\text{cnt}$$$ has to partition all set bits in $$$n$$$.
Since $$$\text{cnt}$$$ partitions the bits of $$$n$$$, there will be $$$i$$$ which has it's most significant bit. This means that $$$2\text{cnt}_i > n$$$, so $$$i$$$ will always be the median.
Suppose there are $$$p$$$ non-zero elements in $$$\text{cnt}$$$. We can partition all set bits of $$$n$$$ into $$$p$$$ non-empty subsequences and then choose which of the $$$m$$$ numbers will occur.
The only time we use the value of $$$n$$$ is when we partition all of it's set bits into subsequences. That means that the answer only depends on the number of set bits in $$$n$$$, not on $$$n$$$ itself.
So let's fix $$$p$$$ as the number of non-zero elements in $$$\text{cnt}$$$ and $$$x$$$ as the median. Denote $$$b$$$ as the number of set bits in $$$n$$$. There are $$$S(b, p)$$$ ways to partition the bits into $$$p$$$ non-empty subsequences, where $$$S$$$ denotes Stirling number of the second kind. There are $$$\binom{x}{p - 1}$$$ ways to choose which other elements will have non-zero $$$\text{cnt}$$$, because the median will always have the largest value and non-zero $$$\text{cnt}_i$$$ must be non-decreasing.
The answer is then $$$\oplus_{p = 1}^b \oplus_{x = 0}^{m - 1} \left(S(b, p) \bmod 2\right) \cdot \left(\binom{x}{p - 1} \bmod 2\right) \cdot x$$$, which we can calculate in $$$O(km)$$$, which solves the easy version.
To solve the hard version we can use Lucas's theorem again to get that the contribution of $$$x$$$ to the answer is the XOR of $$$S(b, p + 1) \bmod 2$$$ over all submasks $$$p$$$ of $$$x$$$. We can limit $$$p$$$ to be between $$$0$$$ and $$$b - 1$$$.
That means that only $$$L = \lceil \log_2 b \rceil$$$ last bits of $$$x$$$ determine whether $$$x$$$ contributes something to the answer. We can find which of $$$2^L$$$ of them will have an odd contribution by setting $$$dp_p = S(b, p + 1) \bmod 2$$$, and calculating it's SOS-dp. Then for fixed $$$L$$$ last bits it is easy to find the XOR of all $$$x < m$$$ with those bits.
Note that $$$S(n, k)$$$ is odd iff $$$(n - k) \text{&} \frac{k - 1}{2} = 0$$$, which we can derive from the recurrence, combinatorics, google or OEIS.
This solves the problem in $$$O(b \log b) = O(k \log k)$$$.
#include <bits/stdc++.h>
using namespace std;
int C(int n, int k) {
return (n & k) == k;
}
int S(int n, int k) {
return !(n - k & (k - 1 >> 1));
}
int brute_partition(int n, int m) {
vector<int> cnt;
int ans = 0;
for(int k = 1; k <= n; k++) {
if(!S(n, k)) continue;
for(int median = 1; median < m; median++) {
if(C(median, k - 1)) ans ^= median;
}
}
return ans;
}
void solve() {
int k, m;
string s;
cin >> k >> m >> s;
int n = 0;
for(auto &i : s) n += i & 1;
int ans = brute_partition(n, m);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}
#include <bits/stdc++.h>
using namespace std;
int S(int n, int k) {
return !(n - k & (k - 1 >> 1));
}
int get(int n, int m) {
int L = __lg(n) + 1;
int up = 1 << L;
vector<int> dp(up);
for(int i = 0; i < n; i++) dp[i] = S(n, i + 1);
for(int j = 0; j < L; j++) {
for(int i = 0; i < up; i++) {
if(i >> j & 1) dp[i] ^= dp[i ^ (1 << j)];
}
}
int ans = 0;
for(int lst = 0; lst < up && lst < m; lst++) {
if(!dp[lst]) continue;
int cnt = m - 1 - lst >> L;
if(cnt & 1 ^ 1) ans ^= lst;
if(cnt % 4 == 0) ans ^= cnt << L;
else if(cnt % 4 == 1) ans ^= 1ll << L;
else if(cnt % 4 == 2) ans ^= cnt + 1 << L;
else ans ^= 0;
}
return ans;
}
void solve() {
int k, m;
string s;
cin >> k >> m >> s;
int n = 0;
for(auto &i : s) n += i & 1;
int ans = get(n, m);
cout << ans << '\n';
}
signed main() {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int ttt = 1;
cin >> ttt;
while(ttt--) {
solve();
}
}