I am using -Werror=uninitialized locally in g++ args. It prevents me from bugs like this
int x;
++x;
But today I realized that my typical code of dfs on tree passes this check
vector<int> tin(n);
int tn;
function<void(int, int)> go = [&](int v, int p) {
tin[v] = tn++;
...
};
So after playing with lines of code I came to this successfully compiled code
int n = 100;
vector<vector<int>> g(n);
int tn;
++tn; //HELLO WHERE IS MY CE???
function<void()> f = [&] {
cout << tn << endl;
};
f();
What interesting is that commenting vector g will result a compilation error. Replacing std::function to lambda will result a compilation error. Moving g under ++tn will result a compilation error...
I am very tilted now. Mike please add g++14 with "deducing this" support...










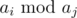 , то переберём в цикле по
, то переберём в цикле по 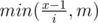 . Тем самым итоговая сложность —
. Тем самым итоговая сложность — 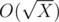 . Как посчитать делители делителей? Нужно знать, что для данных в задаче ограничений на
. Как посчитать делители делителей? Нужно знать, что для данных в задаче ограничений на 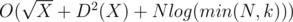 .
.
