Suppose $$$0 <= r <= 1$$$ and $$$1 <= n <= 10^9$$$ times we turn $$$r$$$ into $$$3r/(r+2)$$$.
Example: $$$r = 27/47$$$.
$$$n = 1, r = 27/47 => r = 81/121$$$
$$$n = 2, r = 81/121 => r = 243/323$$$
$$$n = 3, r = 243/323 => r = 729/889$$$
Is this process reducible to a formula?
P.S. This problem is not from a contest, but a subproblem of an assignment on MIT OpenCourseWare. (5th problem, solving for an arbitrary number of 1's)
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
33:29:16
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
$$$a_1 = 1$$$
$$$a_2 = 5$$$
$$$a_n = a_{n-1} + n^2(a_{n-2}+1)$$$
Prove $$$a_n=(n+1)!-1$$$
P.S. Original problem
Чтобы это:
int n;
int m;
int k;
int get(int x) {
return (n + m * x) / k;
}
Превратилось в:
namespace Fast {
int n;
int m;
int k;
int get(int x) {
return (n + m * x) / k;
}
}
Я искал в интернете, но не нашел, подскажите пожалуйста.
Given 3 permutations of equal lengths n ≤ 105, let's call them A, B and C.
Find number of such i-s that there's no such j, that (Ai > Aj and Bi > Bj and Ci > Cj)
Question is solved, please ignore this post
Why if xor sum of segment is equal to sum of segment, this condition is also satisfied for all subsegments of original segment?
I know that it's true when all bits in numbers are unique, but is it the only case when it's true, and if it is, then why?
Given an array of n positive integers called a
For each of q queries which are described with integers 1 ≤ l ≤ r ≤ n, output xor of unique values in segment(l, r), i.e. if x1, x2, x3, ..., xk is set of unique values from al, al + 1, al + 2, ..., ar - 2, ar - 1, ar, then output x1 xor x2 xor x3 xor ... xor xk
1 ≤ n, q ≤ 106
for all i, 1 ≤ ai ≤ 109
TL: 3.5 seconds
ML: 256 megabytes
How to solve it?
If it's possible, I'd like a solution which uses some of data structures listed below:
Segment Tree
Binary Rise/Lift
Trie
Merge Sort Tree
Problem was solved!
Input is consist of 1 ≤ q ≤ 2 * 104 queries every of which are described with single positive integer n not exceeding 4 * 106.
Output is to print for each query: 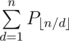
Where:
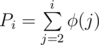
⌊x⌋ = whole part of number, i.e. max integer which's ≤ x
φ(x) is Euler Totient Function
OK, I can previously calculate phis of all numbers from 1 to 4 * 106 and Pi for any i, 1 ≤ i ≤ 4 * 106 in O(nlogn), but what's then? I don't know how to further optimize solution, because it is TLE with O(n) complexity per query.
Please, help me!
| Название |
|---|










