^_^
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
6 days
Register now »
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
We invite you to participate in CodeChef’s Starters 93, this Wednesday, 7th June, rated for all coders.
Time: 8:00 PM — 10:00 PM IST
Note that the duration is 2 hours. Read about the recent CodeChef changes here.
Joining us on the problem setting panel are:
Setters: Kanhaiya notsoloud1 Mohan, Likhon5, Saksham sakshamm123 Mahajan, Shivansh ShivanshJ Jaiswal, Andrei Sho Alexandru, Divyesh divyesh_11 Jivani, Mostafa Beevo Alaa, Tushar CODE_LOVER4655 Singhal
Testers: Nishank IceKnight1093 Suresh
Video Editorialists: Madhav jhamadhav Jha, Suraj jhasuraj01 Jha, Jwala jwalapc, Adhish ak2006 Kancharla, Pravin pravin_as Shankhapal
Text Editorialists: Nishank IceKnight1093 Suresh
Statement Verifier: Kanhaiya notsoloud1 Mohan
Contest Admin: Jatin rivalq Garg
Written editorials will be available for all on discuss.codechef.com. Pro users can find the editorials directly on the problem pages after the contest.
The video editorials of the problems will be available for all users for 1 day as soon as the contest ends, after which they will be available only to Pro users.
We’re hiring! If you’d like to intern at CodeChef as a Learning Content Creator, click here.
Also, if you have some original and engaging problem ideas, and you’re interested in them being used in CodeChef's contests, you can share them here.
Are you ready to dance to the rhythm of Ariana Grande's songs while coding? We sure are! Join us for an unparalleled contest experience. And before you go, drop your favorite Ariana Grande song in the comments. Let's see which tune gets the most love!
I hope you all liked the round. Please share your feedback in the comments section.
1747A — Two Groups
How about putting all positive numbers in one group and negative in second group
Let $$$S$$$ denotes sum of element of array $$$a$$$.
Claim: Answer is $$$|S|$$$.
Proof: Let sum of all positive elements is $$$S_{pos}$$$ and sum of all negative elements $$$S_{neg}$$$. Put all positive numbers in first group and negative numbers in second group. We get $$$||S_{pos}| - |S_{neg}|| = |S|$$$.
Let's prove that we can not do better than that. Let $$$S_1$$$ denotes sum of elements of first group and $$$S_2$$$ denotes sum of elements of second group. We have $$$|S_1| - |S_2| \leq |S_1 + S_2| = |S|$$$. Hence $$$|S|$$$ is the upperbound for the answer.
// Jai Shree Ram
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define ll long long
#define int long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define endl "\n"
#define x first
#define y second
#define gcd(a,b) __gcd(a,b)
#define mem1(a) memset(a,-1,sizeof(a))
#define mem0(a) memset(a,0,sizeof(a))
#define sz(a) (int)a.size()
#define pii pair<int,int>
#define hell 1000000007
#define elasped_time 1.0 * clock() / CLOCKS_PER_SEC
template<typename T1,typename T2>istream& operator>>(istream& in,pair<T1,T2> &a){in>>a.x>>a.y;return in;}
template<typename T1,typename T2>ostream& operator<<(ostream& out,pair<T1,T2> a){out<<a.x<<" "<<a.y;return out;}
template<typename T,typename T1>T maxs(T &a,T1 b){if(b>a)a=b;return a;}
template<typename T,typename T1>T mins(T &a,T1 b){if(b<a)a=b;return a;}
int solve(){
int n; cin >> n;
int s = 0;
for(int i = 0; i < n; i++){
int x; cin >> x;
s += x;
}
cout << abs(s) << endl;
return 0;
}
signed main(){
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#ifdef SIEVE
sieve();
#endif
#ifdef NCR
init();
#endif
int t=1;cin>>t;
while(t--){
solve();
}
return 0;
}
1747B — BAN BAN
Instead of subsequences solve for substrings. That is there should not be any substring $$$\texttt{BAN}$$$ after performing operations.
In one operation you can destroy atmost $$$2$$$ substrings. Find minimum operations to destroy $$$n$$$ substrings.
$$$\left \lceil\frac{n}{2}\right \rceil $$$
Congrats, you have solved for subsequences also!
No subsequences of string $$$\texttt{BAN}$$$ would also mean no substrings of $$$\texttt{BAN}$$$ in original string. Let minimum number of operations to have no substrings of $$$\texttt{BAN}$$$ be $$$x$$$, it would be also be the lower bound for having no subsequences of string $$$\texttt{BAN}$$$.
Claim: $$$x = \left \lceil\frac{n}{2}\right \rceil$$$.
Proof: Swap $$$i$$$-th $$$\texttt{B}$$$ from start with $$$i$$$-th $$$\texttt{N}$$$ from end for $$$1 \leq i \leq \left \lceil\frac{n}{2}\right \rceil$$$. We can see that, no substrings of $$$\texttt{BAN}$$$ exists after performing $$$ \left \lceil\frac{n}{2}\right \rceil$$$ operations. Since we can only destroy atmost $$$2$$$ substrings in one operations, $$$\left \lceil\frac{n}{2}\right \rceil$$$ is minimum possible.
Now if you see clearly, after performing above operations, there does not exist any subsequence of string $$$\texttt{BAN}$$$ in original string. Hence $$$\left \lceil\frac{n}{2}\right \rceil$$$ is also the answer for the original problem.
// Jai Shree Ram
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define ll long long
#define int long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define endl "\n"
#define x first
#define y second
#define gcd(a,b) __gcd(a,b)
#define mem1(a) memset(a,-1,sizeof(a))
#define mem0(a) memset(a,0,sizeof(a))
#define sz(a) (int)a.size()
#define pii pair<int,int>
#define hell 1000000007
#define elasped_time 1.0 * clock() / CLOCKS_PER_SEC
template<typename T1,typename T2>istream& operator>>(istream& in,pair<T1,T2> &a){in>>a.x>>a.y;return in;}
template<typename T1,typename T2>ostream& operator<<(ostream& out,pair<T1,T2> a){out<<a.x<<" "<<a.y;return out;}
template<typename T,typename T1>T maxs(T &a,T1 b){if(b>a)a=b;return a;}
template<typename T,typename T1>T mins(T &a,T1 b){if(b<a)a=b;return a;}
int solve(){
int n; cin >> n;
cout << n/2 + n % 2 << endl;
int l = 1, r = 3*n;
while(l < r){
cout << l << " " << r << endl;
l += 3;
r -= 3;
}
return 0;
}
signed main(){
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#ifdef SIEVE
sieve();
#endif
#ifdef NCR
init();
#endif
int t=1;cin>>t;
while(t--){
solve();
}
return 0;
}
1747C — Swap Game
Divide problem into two different cases. When $$$a_1 \gt \min(a)$$$ and when $$$a_1 = \min(a)$$$.
You do not need more hints to solve the problem.
Case 1: $$$a_1 \gt \min(a)$$$
$$$\texttt{Alice}$$$ can force the $$$\texttt{Bob}$$$ to always decrease the minimum element by always choosing minimum element of $$$a$$$ in her turn. Where as $$$\texttt{Bob}$$$ can not do much, all other elements he would swap with would be greater than or equal to $$$\min(a)$$$. Even if there exists multiple minimums in $$$a$$$, In first move $$$\texttt{Alice}$$$ would decrease from $$$a_1$$$, hence in this case $$$\texttt{Alice}$$$ would always win.
Case 2: $$$a_1 = \min(a)$$$
In this case optimal startegy for $$$\texttt{Bob}$$$ would be to always chhose minimum element of the array, which is $$$a_1$$$. $$$\texttt{Alice}$$$ would always be swapping the element greater than $$$a_1$$$ in her turn, hence in the case $$$\texttt{Bob}$$$ would always win
// Jai Shree Ram
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define ll long long
#define int long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define endl "\n"
#define x first
#define y second
#define gcd(a,b) __gcd(a,b)
#define mem1(a) memset(a,-1,sizeof(a))
#define mem0(a) memset(a,0,sizeof(a))
#define sz(a) (int)a.size()
#define pii pair<int,int>
#define hell 1000000007
#define elasped_time 1.0 * clock() / CLOCKS_PER_SEC
template<typename T1,typename T2>istream& operator>>(istream& in,pair<T1,T2> &a){in>>a.x>>a.y;return in;}
template<typename T1,typename T2>ostream& operator<<(ostream& out,pair<T1,T2> a){out<<a.x<<" "<<a.y;return out;}
template<typename T,typename T1>T maxs(T &a,T1 b){if(b>a)a=b;return a;}
template<typename T,typename T1>T mins(T &a,T1 b){if(b<a)a=b;return a;}
int solve(){
int n; cin >> n;
vector<int> a(n);
for(auto &i:a)cin >> i;
sort(a.begin() + 1,a.end());
cout << (a[0] > a[1] ? "Alice" : "Bob") << endl;
return 0;
}
signed main(){
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#ifdef SIEVE
sieve();
#endif
#ifdef NCR
init();
#endif
int t=1;cin>>t;
while(t--){
solve();
}
return 0;
}
1747D — Yet another Problem
Forget queries, they are just here to make problem look complicated. Solve for $$$q = 1$$$.
XOR of array does not change after operations. Hence if initially XOR is not equal to $$$0$$$, answer is $$$-1$$$. Is this condition sufficient?
No, We need one more condition
There must exist some prefix of odd size, such that xor of elements of that prefix is $$$0$$$.
First forget queries, solve for single array $$$a$$$.
Let's make some observations.
Xor of array does not change after each operation
Look at the set of prefix XORs while doing operations. Its size always decreases or remains same after each operation. Infact we can further reduce it to parities. Let $$$S_{0}$$$, $$$S_{1}$$$ be sets of prefix XOR's of parities $$$0$$$ and $$$1$$$ respectively. After each operation new sets $$$S'_{0}$$$, $$$S'_{1}$$$ will be subsets of $$$S_{0}$$$ and $$$S_1$$$ respectively.
So necessary conditions for answer to exist is that xor of array should be $$$0$$$ and $$$S_{1}$$$ should contains $$$0$$$.
Now comes to minimum operations.
Claim: If above conditions are satisfied, its always possible to make all elements $$$0$$$ in less than or equal to $$$2$$$ operations
Proof: Let length of array be $$$n$$$.
Case 1: $$$n$$$ is odd
Just apply the operation on whole array.
Case 2: $$$n$$$ is even
There will exists some odd size prefix $$$j$$$ such that xor of its elements is $$$0$$$. Apply operation on $$$[1,j]$$$ and $$$[j + 1,n]$$$. It can happen that $$$j = 1$$$ or $$$j = n - 1$$$, in that case we only need one operation, because other remaining element would already be equal to $$$0$$$.
To solve for queries, you just need to check for odd prefix, which can be done using some data structure like $$$\texttt{std::map}$$$ or $$$\texttt{std::set}$$$ in C++. Do not forget to check the case when all elements are already $$$0$$$.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y < x) x = y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x < y) x = y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 3000
#endif
int _runtimeTerror_()
{
int n, Q;
cin >> n >> Q;
map<int, int> odd, even;
vector<int> last_nz(n + 1, 0), last(n + 1, -1), pxor(n + 1, 0);
vector<int> a(n + 1);
even[0] = 0;
int cur = 0;
for(int i=1;i<=n;++i) {
cin >> a[i];
cur ^= a[i];
pxor[i] = cur;
if(a[i] == 0) {
last_nz[i] = last_nz[i - 1];
}
else {
last_nz[i] = i;
}
if(i & 1) {
if(even.count(cur)) {
last[i] = even[cur];
}
odd[cur] = i;
}
else {
if(odd.count(cur)) {
last[i] = odd[cur];
}
even[cur] = i;
}
}
while(Q--) {
int l, r;
cin >> l >> r;
if(pxor[l - 1] != pxor[r]) {
cout << "-1\n";
}
else if(last_nz[r] < l) {
cout << "0\n";
}
else if(r % 2 == l % 2) {
cout << "1\n";
}
else if(a[l] == 0 or a[r] == 0) {
cout << "1\n";
}
else if(last[r] >= l) {
cout << "2\n";
}
else {
cout << "-1\n";
}
}
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initncr();
#endif
int TESTS = 1;
//cin >> TESTS;
while(TESTS--) {
_runtimeTerror_();
}
return 0;
}
1747E — List Generation
Change your point of view from array to grid. Think of pair of arrays as paths in grid of size $$$(n + 1) \times (m + 1)$$$.
First try counting number of good pair of arrays.
Number of good pairs of arrays comes out to be $$$\sum\limits_{k = 0}{k = \min(n,m} \binom{n}{k} \cdot \binom{m}{k} \cdot 2^{n + m - k - 1}$$$
Given problem is equivalent to:
You are currently at cell $$$(0,0)$$$. From any cell $$$(x,y)$$$ you can jump to cell $$$(x',y')$$$ such that $$$x \leq x' \leq n$$$ , $$$y \leq y' \leq m$$$ and $$$(x,y) \neq (x',y')$$$. Find sum of number of visited cells over all paths starting from $$$(0,0)$$$ and ending at $$$(n,m)$$$. Denote the required value by $$$f(n,m)$$$.
Directly thinking in $$$2$$$ dimensions is difficult, lets first solve for case when $$$n = 0$$$ or $$$m = 0$$$. WLOG, assuming $$$m = 0$$$. We can solve this case using some binomials.
$$$f(n,0) = 2^{n - 1} \cdot \frac{n + 3}{2}$$$, $$$n \gt 0$$$.
Now, we can divide all possible paths from $$$(0,0)$$$ to $$$(n,m)$$$ into several classes of one dimensional paths.
These classes are defined by what I call breakpoints. When we passes the breakpoint we turns right. Hence we can group paths by fixing the number of breakpoints.
WLOG, Assuming $$$n \geq m$$$. For $$$k$$$ breakpoints there are $$$\binom{n}{k} \cdot \binom{m}{k}$$$ ways to select for $$$0 \leq k \leq m $$$. For a path with $$$k$$$ breakpoints, $$$n + m - k$$$ points are optional, that is there will exist $$$2^{n + m - k}$$$ paths with $$$k$$$ breakpoints. It is not difficult to see that sum of number of visited cells over paths with $$$k$$$ breakpoints turned out to be $$$f(n + m - k,0) + 2^{n + m - k - 1}\cdot k$$$. Hence we can write $$$f(n,m) = \sum\limits_{k = 0}^{m} \binom{n}{k} \cdot \binom{m}{k} \cdot (f(n + m - k,0) + 2^{n + m - k - 1}\cdot k)$$$
Time complexity of the solution would be $$$\mathcal{O}(\min(n,m))$$$
// Jai Shree Ram
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,n) for(int i=a;i<n;i++)
#define ll long long
#define int long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define endl "\n"
#define x first
#define y second
#define gcd(a,b) __gcd(a,b)
#define mem1(a) memset(a,-1,sizeof(a))
#define mem0(a) memset(a,0,sizeof(a))
#define sz(a) (int)a.size()
#define pii pair<int,int>
#define hell 1000000007
#define elasped_time 1.0 * clock() / CLOCKS_PER_SEC
template<typename T1,typename T2>istream& operator>>(istream& in,pair<T1,T2> &a){in>>a.x>>a.y;return in;}
template<typename T1,typename T2>ostream& operator<<(ostream& out,pair<T1,T2> a){out<<a.x<<" "<<a.y;return out;}
template<typename T,typename T1>T maxs(T &a,T1 b){if(b>a)a=b;return a;}
template<typename T,typename T1>T mins(T &a,T1 b){if(b<a)a=b;return a;}
const int MOD = hell;
struct mod_int {
int val;
mod_int(long long v = 0) {
if (v < 0)
v = v % MOD + MOD;
if (v >= MOD)
v %= MOD;
val = v;
}
static int mod_inv(int a, int m = MOD) {
int g = m, r = a, x = 0, y = 1;
while (r != 0) {
int q = g / r;
g %= r; swap(g, r);
x -= q * y; swap(x, y);
}
return x < 0 ? x + m : x;
}
explicit operator int() const {
return val;
}
mod_int& operator+=(const mod_int &other) {
val += other.val;
if (val >= MOD) val -= MOD;
return *this;
}
mod_int& operator-=(const mod_int &other) {
val -= other.val;
if (val < 0) val += MOD;
return *this;
}
static unsigned fast_mod(uint64_t x, unsigned m = MOD) {
#if !defined(_WIN32) || defined(_WIN64)
return x % m;
#endif
unsigned x_high = x >> 32, x_low = (unsigned) x;
unsigned quot, rem;
asm("divl %4\n"
: "=a" (quot), "=d" (rem)
: "d" (x_high), "a" (x_low), "r" (m));
return rem;
}
mod_int& operator*=(const mod_int &other) {
val = fast_mod((uint64_t) val * other.val);
return *this;
}
mod_int& operator/=(const mod_int &other) {
return *this *= other.inv();
}
friend mod_int operator+(const mod_int &a, const mod_int &b) { return mod_int(a) += b; }
friend mod_int operator-(const mod_int &a, const mod_int &b) { return mod_int(a) -= b; }
friend mod_int operator*(const mod_int &a, const mod_int &b) { return mod_int(a) *= b; }
friend mod_int operator/(const mod_int &a, const mod_int &b) { return mod_int(a) /= b; }
mod_int& operator++() {
val = val == MOD - 1 ? 0 : val + 1;
return *this;
}
mod_int& operator--() {
val = val == 0 ? MOD - 1 : val - 1;
return *this;
}
mod_int operator++(int32_t) { mod_int before = *this; ++*this; return before; }
mod_int operator--(int32_t) { mod_int before = *this; --*this; return before; }
mod_int operator-() const {
return val == 0 ? 0 : MOD - val;
}
bool operator==(const mod_int &other) const { return val == other.val; }
bool operator!=(const mod_int &other) const { return val != other.val; }
mod_int inv() const {
return mod_inv(val);
}
mod_int pow(long long p) const {
assert(p >= 0);
mod_int a = *this, result = 1;
while (p > 0) {
if (p & 1)
result *= a;
a *= a;
p >>= 1;
}
return result;
}
friend ostream& operator<<(ostream &stream, const mod_int &m) {
return stream << m.val;
}
friend istream& operator >> (istream &stream, mod_int &m) {
return stream>>m.val;
}
};
#define NCR
const int N = 5e6 + 5;
mod_int fact[N],inv[N],invv[N];
void init(int n=N){
fact[0]=inv[0]=inv[1]=1;
invv[0] = invv[1] = 1;
rep(i,1,N)fact[i]=i*fact[i-1];
rep(i,2,N){
invv[i] = (MOD - MOD/i)*invv[MOD % i];
inv[i] = invv[i]*inv[i - 1];
}
}
mod_int C(int n,int r){
if(r>n || r<0)return 0;
return fact[n]*inv[n-r]*inv[r];
}
int solve(){
int n,m; cin >> n >> m;
if(m > n)swap(n,m);
auto brute = [&](){
vector<vector<mod_int>>dp(n + 1,vector<mod_int>(m + 1));
vector<vector<mod_int>>exp(n + 1,vector<mod_int>(m + 1));
dp[0][0] = 1;
exp[0][0] = 0;
for(int i = 0; i <= n; i++){
for(int j = 0; j <= m; j++){
if(i + j == 0)continue;
for(int x = 0; x <= i; x++){
for(int y = 0; y <= j; y++){
if(x + y == i + j)continue;
dp[i][j] += dp[x][y];
exp[i][j] += (exp[x][y] + dp[x][y]);
}
}
}
}
return exp[n][m] + dp[n][m];
};
auto correct = [&](){
mod_int in = mod_int(2).inv();
auto d = [&](int x){
mod_int val = x + 1;
return val * in;
};
mod_int ans = 0;
mod_int pw = mod_int(2).pow(n + m);
for(int i = 0; i <= m; i++){
pw *= in;
ans += C(n,i)*C(m,i)*pw*(i + d(n + m - i) + 1);
}
return ans;
};
cout << correct() << endl;
return 0;
}
signed main(){
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#ifdef SIEVE
sieve();
#endif
#ifdef NCR
init();
#endif
int t=1;cin>>t;
while(t--){
solve();
}
return 0;
}
Hi Codeforces!
I am pleased to invite you to Adhocforces, Mathforces Codeforces Round #832 (Div. 2), which will take place on Friday, Nov 4, 2022 at 14:35 UTC. You will be given 5 problems and 2 hours to solve them.
The round will be rated for participants of Division 2 with a rating lower than 2100. Division 1 participants can participate unofficially in the round.
All problems in this round were prepared by me and CoderAnshu.
I would like to thank:
- antontrygubO_o for coordination of the round.
- ffao, Everule, Andreasyan, koderkushy, nor, AlperenT, the_hyp0cr1t3, Runtime-Terr0r, sp005, 18o3, KingRayuga, Scythe and sus for testing this round and giving really valuable feedback.
- MikeMirzayanov for the amazing Codeforces and Polygon platforms!
- You for participating.
The score distribution will be announced shortly before the round (or earlier).
Good luck and have fun! See you in the standings.
UPD 1:
Scoring distribution: 500 — 1000 — 1250 — 1750 — 2500
UPD 2:
I am flying to dhaka so will post editorials later.
UPD 3:
Congratulations to our winners!
Overall:
Div 2:
UPD 4: Editorial for A to C has been posted, will post D,E soon.
UPD 5: Editorial for D is posted.
UPD 6: Finally editorial for E is posted.
I hope you all liked the round. Please share your feedback in the comments section.
1682A — Palindromic Indices
Read the statement carefully!! The given string is a palindrome.
Let's remove some index $$$i$$$ from the first half of $$$s$$$ and check whether the resulting string is a palindrome or not, the other half has the same approach. The prefix of length $$$i-1$$$ already matches with the suffix of the same length because the initial string was a palindrome, so we just need to check if $$$t = s[i + 1 \ldots n - i + 1]$$$ is a palindrome.
For $$$t$$$ to be a palindrome, $$$s_{n - i + 1}$$$ should be equal to $$$s_{i + 1}$$$ which was initially equal to $$$s_{n - i}$$$, again which should be equal to $$$s_{i + 2}$$$ and this goes on. Here we can see that $$$s_i = s_{i + 1} \ldots = s_{n - i + 1}$$$. So the answer is simply equal to the number of contiguous same characters in the center of the string which can be calculated in $$$\mathcal{O(n)}$$$.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y < x) x = y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x < y) x = y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2401
#endif
int _runtimeTerror_()
{
int n;
cin >> n;
string s;
cin >> s;
int cnt = 0;
for(int i=(n-1)/2;i>=0;--i) {
if(s[i] == s[(n - 1) / 2]) {
++cnt;
}
else {
break;
}
}
cout << 2 * cnt - (n & 1) << "\n";
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initncr();
#endif
int TESTS = 1;
cin >> TESTS;
while(TESTS--) {
_runtimeTerror_();
}
return 0;
}
1682B — AND Sorting
You must have to make at least one swap on the elements which are not at their correct positions initially. So $$$X$$$ must be a submask of all elements which are not at their correct positions.
What is the maximum possible value of $$$X$$$ from Hint $$$1$$$? It is the bitwise AND of all elements which are not at their correct positions. It turns out that this value is achievable too.
We always have to make at least one swap for the elements which are not at their correct positions. Hence an upper bound of answer would be the bitwise AND of those elements. Let the value be $$$X$$$. It turns out that the given permutation is $$$X$$$-sortable.
Proof:
First, notice that $$$X$$$ would always be present in $$$p$$$. Let $$$pos_x$$$ be the position of $$$X$$$ in $$$p$$$ initially. Let's say at some point we want to swap two values $$$p_i$$$ and $$$p_j$$$, then $$$p_i$$$ and $$$p_j$$$ would always be a supermask of $$$X$$$ i.e. $$$p_i$$$ & $$$X = X$$$ and $$$p_j$$$ & $$$X = X$$$. We can make the following moves to swap $$$p_i$$$ and $$$p_j$$$ without disturbing any other element.
- Swap values at indices $$$i$$$ and $$$pos_x$$$.
- Swap values at indices $$$i$$$ and $$$j$$$.
- Swap values at indices $$$j$$$ and $$$pos_x$$$.
It can be seen that in every swap the bitwise AND of two values which we are swapping is always $$$X$$$. Hence we can swap any two values which were not at their correct positions, therefore we can sort the permutation $$$p$$$.
Overall Complexity: $$$\mathcal{O(n)}$$$.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y < x) x = y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x < y) x = y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2401
#endif
int _runtimeTerror_()
{
int n;
cin >> n;
int ans = (1 << 30) - 1;
for(int i=0;i<n;++i) {
int x;
cin >> x;
if(x != i) {
ans &= x;
}
}
cout << ans << "\n";
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initncr();
#endif
int TESTS = 1;
cin >> TESTS;
while(TESTS--) {
_runtimeTerror_();
}
return 0;
}
1682C — LIS or Reverse LIS?
Let $$$\text{LDS}(a)$$$ be the longest strictly decreasing subsequence of $$$a$$$, then $$$\text{LIS}(a')$$$ = $$$\text{LDS}(a)$$$.
There can be at most one index common between $$$\text{LIS}(a)$$$ and $$$\text{LDS}(a)$$$.
Let's make a small observation:
- There can be at most one index common to both $$$\text{LIS}(a)$$$ and $$$\text{LDS}(a)$$$.
If some element $$$x$$$ occurs $$$\geq 2$$$ times, then one of its occurrences can be included in $$$\text{LIS}(a)$$$ and another one in $$$\text{LDS}(a)$$$, and all the remaining occurrences are of no use because none of them can contain 2 equal elements.
If some element $$$x$$$ is a singleton i.e. the frequency of $$$x$$$ in $$$a$$$ is $$$1$$$, then it can have $$$3$$$ positions
- In $$$\text{LIS}(a)$$$ only.
- In $$$\text{LDS}(a)$$$ only.
- The only common element of $$$\text{LIS}(a)$$$ and $$$\text{LDS}(a)$$$.
It can be seen that it is always optimal to choose some singleton as the only common element (if available) because those with frequency $$$\geq 2$$$ can easily contribute $$$1$$$ to both $$$\text{LIS}(a)$$$ and $$$\text{LDS}(a)$$$ easily.
Let $$$t$$$ be the number of elements having frequency $$$\geq 2$$$ and $$$s$$$ be the number of singletons in $$$a$$$. The singletons should be divided equally among $$$\text{LIS}(a)$$$ and $$$\text{LDS}(a)$$$ with one of them given to both, if available.
Hence, the answer is $$$t + \lceil \frac{s}{2} \rceil$$$.
The values $$$s$$$ and $$$t$$$ can be found using some data structure like $$$\text{std:map}$$$ in C++ in $$$\mathcal{O}(n\log(n))$$$.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y < x) x = y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x < y) x = y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2401
#endif
int _runtimeTerror_()
{
int n;
cin >> n;
map<int, int> mp;
for(int i=1;i<=n;++i) {
int x;
cin >> x;
++mp[x];
}
int single = 0, doble = 0;
for(auto &[i, j]:mp) {
single += j == 1;
doble += j > 1;
}
cout << doble + (single + 1) / 2 << "\n";
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initncr();
#endif
int TESTS = 1;
cin >> TESTS;
while(TESTS--) {
_runtimeTerror_();
}
return 0;
}
1682D — Circular Spanning Tree
What are the mandatory conditions on string $$$s$$$ for a tree to be possible?
If there are no odd degree vertices or the count of odd degree vertices is odd, then it is impossible to construct any tree. It turns out that these conditions are sufficient too.
Let's check some cases when it is not possible to construct the answer-
- When all vertices have an even degree, then there is no way to generate a tree because every tree contains at least $$$2$$$ leaves.
- When there are an odd number of vertices with odd degrees, then there is no tree possible because the sum of degrees must be even.
It turns out that it is always possible to construct a tree if none of the above is true.
The following construction works -
Select some vertex $$$i$$$ such that the previous vertex of $$$i$$$ (assumed cyclically) has an odd degree i.e. $$$s_{i - 1} = 1$$$. Clearly, such a vertex always exists.
Now left rotate $$$s$$$, $$$i - 1$$$ times such that the selected vertex is now at index $$$1$$$. Note that after the rotation $$$s_n$$$ will become $$$1$$$. Now we can see that $$$s[2\ldots n]$$$ can be divided into several segments such that each segment ends with some vertex having an odd degree. And each segment should contain exactly one vertex with an odd degree. So $$$s[2 \ldots n] = [0\ldots 1][0\ldots 1] \ldots [0\ldots 1]$$$ where $$$0$$$ may appear $$$0$$$ times. Connect vertex $$$1$$$ to the starting vertex of each segment and connect adjacent vertices inside each segment. It can be clearly seen that edges will never intersect internally. The only thing we need to verify is the degree constraints.
Proof:
- The degree condition is valid for each segment, as each vertex with an even degree is connected with $$$2$$$ other vertices and the last vertex with an odd degree will be connected to only one vertex i.e it's previous one or vertex $$$1$$$ if it was only on its segment.
- Let $$$cnt_1$$$ be the number of vertices with odd degree. If $$$s_1 = 1$$$, then there will be $$$cnt_1 - 1$$$ segments which is an odd number, hence vertex $$$1$$$ will be connected to odd number of vertices. If $$$s_1 = 0$$$, then there will be $$$cnt_1$$$ segments which is an even number, hence vertex $$$1$$$ will be connected to even number of vertices.
Note that we renumbered the vertices during rotation which should be handled in implementation.
The intuition for the above approach comes from the case when all $$$s_i$$$ are $$$1$$$ in which we create a star network.
Overall complexity: $$$\mathcal{O(n)}$$$.
#include<bits/stdc++.h>
using namespace std;
#define all(v) v.begin(),v.end()
#define endl "\n"
int solve(){
int n; cin >> n;
string s; cin >> s;
auto cnt = count(all(s),'1');
if(cnt == 0 or cnt & 1){
cout << "NO" << endl;
return 0;
}
auto inc = [&](int j){
return (j + 1)%n;
};
cout << "YES" << endl;
for(int p = 1; p < n; p++){
if(s[p - 1] == '1'){
auto i = inc(p);
while(i != p){
int j = i;
int prev = p;
while(j != p){
cout << prev + 1 << " " << j + 1 << endl;
prev = j;
j = inc(j);
if(s[prev] == '1')break;
}
i = j;
}
return 0;
}
}
return 0;
}
signed main(){
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#ifdef SIEVE
sieve();
#endif
#ifdef NCR
init();
#endif
int t=1;cin>>t;
while(t--){
solve();
}
return 0;
}
1682E — Unordered Swaps
One way of solving permutation problems is to look at permutation cycles. Let's decompose our permutation into cycles, then it's easy to see that each cycle can be solved independently because we have to sort the permutation in a minimum number of moves which isn't possible if two cycles are merged at any instant.
Let's look at one cycle only, whose vertices are numbered from $$$1$$$ to $$$n$$$ in the orientation of cycle i.e the cycle is $$$1 \rightarrow 2 \rightarrow \ldots \rightarrow n \rightarrow 1$$$. Also assume that we only have swaps $$$(x, y)$$$ that are relevant to this cycle.
It is known that we can sort a cycle of size $$$n$$$ in $$$n - 1$$$ moves and it is the minimum number of required moves.
Claim 1: The set of swaps if considered as edges $$$(x, y)$$$ form a tree on the $$$n$$$ vertices of the cycle.
Assume that the edges don't form a tree, then there exist at least two disjoint components let's say $$$S$$$ and $$$T$$$. Now we must be able to make swaps inside $$$S$$$ only, to sort elements in $$$S$$$ which needs that the set {$$$i, i \in S$$$} is same as set {$$$p_i, i \in S$$$} which is not possible by property of permutation cycles. Any cycle of permutation, say $$$C$$$, can't be split further into two sets $$$S$$$ and $$$T$$$ such that both of them can be sorted independently among themselves.
So we must use all the $$$n - 1$$$ edges of the tree in some order to get $$$n$$$ cycles each of size $$$1$$$.
Let's consider any element $$$u$$$ having adjacency list as $$$[x_1, x_2, ..., x_k]$$$ in the order they appear on the cycle if we start moving from $$$u$$$ in the orientation of cycle i.e $$$u \rightarrow u + 1 \rightarrow ... \rightarrow n \rightarrow 1 \rightarrow ... \rightarrow u$$$.
Claim 2: We can never make the swap $$$(u, x_j)$$$ before swap $$$(u, x_i)$$$ if $$$j > i$$$.
If we make the swap $$$(u, x_j)$$$ first, then $$$u$$$ and $$$x_i$$$ will go in different cycles for subsequent operations and we will never be able to use edge $$$(u, x_i)$$$ because it will merge the two different cycles which isn't possible because we are constrained to break a cycle into smaller cycles only.
And if are not able to use edge $$$(u, x_i)$$$ then we will never be able to sort the permutation because we had $$$n - 1$$$ edges all of which were to be used and we wasted $$$1$$$ of them.
Using above claim, for every element $$$u$$$ the order of edges is fixed i.e $$$x_1$$$, then $$$x_2$$$, ..., and finally $$$x_k$$$.
Let's build a directed graph on $$$n - 1$$$ vertices (representing the swaps) where for every element $$$u$$$ we add directed edges $$$(u,x_1) \rightarrow (u,x_2)$$$, ..., $$$(u,x_{k-1}) \rightarrow (u,x_k)$$$.
Since it is guaranteed that the answer will exist i.e a valid sequence of moves exist, hence the topological sorting of the above graph must exist, any of which represents a correct sequence of swaps.
Note that whenever we make a swap that is not violating claim $$$2$$$ for any element $$$u$$$, then there will be no cross edge in two smaller cycles that are going to be formed and those smaller cycles can be further solved independently. Also the order of edges i.e $$$[x_1, x_2, ..., x_k]$$$ is not going to change for any element which ensures that the directed graph we built remains correct even if we remove some appropriate edge.
Hence the answer is simply the topological sort of the graph we built.
Overall Complexity: $$$\mathcal{O(nlog(n))}$$$, $$$nlog(n)$$$ for sorting the edges according to cycle's orientation to get the order $$$[x_1, x_2, ..., x_k]$$$ for every vertex.
Claim: The given swaps considered as edges $$$(x, y)$$$ forms a non-intersecting tree on $$$n$$$ vertices on the circle i.e no two edges intersect internally. Motivation for problem D
Let's say edges $$$(a, b)$$$ and $$$(c, d)$$$ intersect internally in the circle.
WLOG, let's suppose we make swap $$$(a, b)$$$ before swap $$$(c, d)$$$, then $$$c$$$ and $$$d$$$ will go in different cycles as in Claim $$$2$$$ above.
What if you were given any tree on $$$n$$$ vertices and asked to solve the problem with "YES/NO"?
- If the given edges intersect internally in the circle then the answer is "NO" otherwise it's always possible to construct a valid sequence of swaps. This is what the validator of E and checker of D do, try this one, and feel free to discuss in the comments section.
Let's make every edge $$$(u, v)$$$ such that $$$u \lt v$$$, clearly the order of $$$u$$$, $$$v$$$ doesn't matter.
Consider each edge as a segment $$$[u, v]$$$, then the edges of the tree intersect internally if and only if any two segments say $$$[l_1, r_1]$$$ and $$$[l_2, r_2]$$$ satisfies any of the below conditions-
$$$l_1\lt l_2 \lt r_1 \lt r_2$$$
$$$l_2 \lt l_1 \lt r_2 \lt r_1$$$
In the original problem, it was mentioned that there is always a correct sequence of swaps so we claimed that topological sorting must exist and indeed any topological sorting suffices. What if we were given a non-intersecting spanning tree? Can we still claim that there exists a correct move at every step?
Claim: Yes, we can
We need to show that there there is always some edge that can be removed without breaking claim $$$2$$$ above which is the only required condition.
Cycles of length $$$\le 2$$$ are trivial.
Let's represent by $$$u_{next}$$$ the first element of the list $$$[x_1, x_2, ..., x_k]$$$ for $$$u$$$ i.e the closest vertex having an edge with $$$u$$$ in cycle's orientation.
Now, let's start an iteration, start moving from $$$1$$$ and jump to $$$v_{next}$$$ every time when you are at vertex $$$v$$$. Continue this process until you again reach $$$1$$$ or cross over $$$1$$$.
Let the sequence obtained be $$$s$$$ i.e $$$s_1 = 1, s_2, ..., s_k$$$ where on moving further from $$$s_k$$$ we cross/reach $$$1$$$. For simplicity assume $$$k \ge 3$$$, $$$k = 2$$$ is trivial.
It can be shown that $$$(s_{k-1}, s_k)$$$ is the required edge.
$$$s_{k_{next}}$$$ lies between $$$s_{k-1}$$$ and $$$s_k$$$. There are three cases other that this:
$$$s_{k_{next}}$$$ lies between $$$s_k$$$ and $$$1$$$, which is not possible because we would have moved further and $$$s_k$$$ would not be the last element of sequence $$$s$$$.
$$$s_{k_{next}}$$$ = $$$1$$$ which is not possible because it will create a cycle and we are given a tree.
$$$s_{k_{next}}$$$ lies between $$$s_j$$$ and $$$s_{j+1}$$$ for $$$j \le k-2$$$, this is also not possible because then the edges $$$(s_k, s_{k_{next}})$$$ and $$$(s_j, s_{j+1})$$$ will intersect and we are given a non-intersecting tree.
$$$s_{k}$$$ is first element of adjacency list of $$$s_{k-1}$$$ by the definition of $$$v_{next}$$$ and $$$s_{k-1}$$$ is the first element of adjacency list of $$$s_{k}$$$ by above 3 points.
Hence it is safe to make the swap $$$(s_{k-1}, s_{k})$$$.
So the topological sort still works.
This might not be the only proof, if you have some other proofs feel free to discuss them in the comments.
Hope you liked the details!!
Any ideas on how to write a generator for this problem?
Randomly partition the permutation into cycles, so generating swaps for a particular cycle is the main issue.
Let's represent the cycle by an array $$$a$$$ of size $$$n$$$ with cycle as $$$a_1 \rightarrow a_2 \rightarrow ... \rightarrow a_n \rightarrow a_1$$$ Now let's start making random swaps say $$$(a_i, a_j)$$$ to break the cycle, then this generates two smaller cycles -
$$$a_1 \rightarrow a_2 \rightarrow ... \rightarrow a_i \rightarrow a_{j+1} \rightarrow ... \rightarrow a_n \rightarrow a_1$$$.
$$$a_{i+1} \rightarrow ... \rightarrow a_j \rightarrow a_{i+1}$$$.
This can be easily done using treaps :) and then we can use recursion to solve them independently.
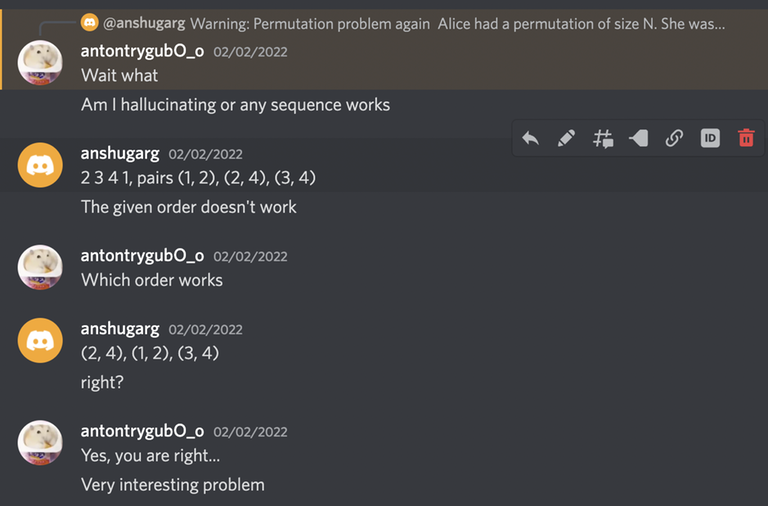
It's very rare!! Atleast first time for us.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y < x) x = y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x < y) x = y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2401
#endif
const int N = 2e5 + 5;
vector<int> t_sort;
int idx[N];
int vs[N];
vector<int> v[N];
bool dfs_sort(int u)
{
vs[u]=2;
for(auto j:v[u])
{
if(vs[j]==2)
return true;
if(vs[j]==0 && dfs_sort(j))
return true;
}
vs[u]=1;
t_sort.push_back(u);
return false;
}
// Returns true if there is a topological sort else returns false
bool top_sort(int n)
{
t_sort.clear();
for(int i=1;i<=n;++i)
vs[i]=0;
for(int i=1;i<=n;++i)
{
if(vs[i]==0)
{
if(dfs_sort(i))
{
t_sort.clear();
return false;
}
}
}
reverse(t_sort.begin(),t_sort.end());
assert(t_sort.size()==n);
for(int i=0;i<n;++i)
idx[t_sort[i]]=i;
return true;
}
int _runtimeTerror_()
{
int n, k;
cin >> n >> k;
vector<int> p(n+1), a(k), b(k);
for(int i=1;i<=n;++i) {
cin >> p[i];
}
vector<vector<pii>> g(n+1);
for(int i=0;i<k;++i) {
int x, y;
cin >> x >> y;
a[i] = x, b[i] = y;
g[x].push_back({y, i + 1});
g[y].push_back({x, i + 1});
}
vector<int> id(n+1);
vector<int> ans;
auto solve = [&](vector<int> &cyc) {
int n = sz(cyc);
if(n == 1) {
return;
}
for(int i=0;i<n;++i) {
id[cyc[i]] = i;
}
auto dist = [&](int x, int y) {
return (id[y] - id[x] + n) % n;
};
vector<int> good;
for(int i:cyc) {
sort(all(g[i]), [&](pii &a, pii &b) {
return dist(i, a.F) < dist(i, b.F);
});
for(int j=1;j<sz(g[i]);++j) {
v[g[i][j-1].S].push_back(g[i][j].S);
}
}
};
vector<bool> vis(n+1);
for(int i=1;i<=n;++i) {
if(vis[i]) {
continue;
}
vector<int> cycle;
int cur = i;
while(!vis[cur]) {
cycle.push_back(cur);
vis[cur] = 1;
cur = p[cur];
}
solve(cycle);
}
top_sort(k);
for(auto i:t_sort) {
cout << i << " ";
}
cout << "\n";
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initncr();
#endif
int TESTS = 1;
//cin >> TESTS;
while(TESTS--) {
_runtimeTerror_();
}
return 0;
}
1682F — MCMF?
Let us suppose we need to calculate the answer for only one query, say complete array i.e $$$a[1:n]$$$.
The scary flow structure in the problem can be reduced as-
Let's replicate each vertex $$$i$$$, $$$|b_i|$$$ times. Then we can see that there will be an equal number of vertices on the left and right side. Now the problem reduces that we have to match these vertices with minimum cost such that the cost of matching $$$i$$$ and $$$j$$$ is $$$|a_i - a_j|$$$.
There are only 2 type of elements (left side and right side) and the following greedy algorithm to match the elements works.
Algorithm: Sort the type $$$1$$$ and $$$2$$$ elements independently and match them in the sorted order.
Assume that two elements from left $$$l_1 \le l_2$$$ are matched with two elements from right $$$r_1 \le r_2$$$ as $$$[l_1, r_2]$$$ and $$$[l_2, r_1]$$$, then it can be easily shown that matching $$$[l_1, r_1]$$$ and $$$[l_2, r_2]$$$ is always more optimal. The proof is left as an excercise to reader.
Since the array $$$a$$$ is given in sorted order, let's use it!!
Let's assume-
Type $$$1$$$ elements are those having $$$b_i \lt 0$$$.
Type $$$2$$$ elements are those having $$$b_i \gt 0$$$.
Now instead of replicating elements $$$|b_i|$$$ times and sorting them independently, let's iterate on array $$$a$$$ from left to right and add the contribution of each element independently. Say we are at index $$$i$$$, and prefix sum of $$$b_i$$$ so far is $$$psum_i$$$, then the following cases arise-
$$$b_i \gt 0$$$, $$$psum_i \ge 0$$$ — There is no unmatched type $$$1$$$ element on the left, so we just add this element's contribution to the answer i.e $$$-b_i \cdot a_i$$$.
$$$b_i \gt 0$$$, $$$psum_i \lt -b_i$$$ — There are more than $$$b_i$$$ unmatched type $$$1$$$ elements on the left, so we match $$$b_i$$$ of them to $$$a_i$$$, adding a contribution of $$$a_i \cdot b_i$$$ to the answer.
$$$b_i \gt 0$$$, $$$psum_i \lt 0$$$ and $$$psum_i \gt -b_i$$$ — There are less than $$$b_i$$$ unmatched elements ($$$= |psum_i|$$$) on the left, so we match those with equal number of $$$a_i$$$ and remaining are propagated further, adding a contribution of $$$|psum_i| * a_i - (b_i - |psum_i|) * a_i$$$, where the positive term comes from those matching with previous unmatched elements and the negative term comes from those that are going to be left unmatched.
Similar cases are there for $$$b_i \lt 0$$$.
Ok so now we can easily solve the problem for one query in $$$O(n)$$$.
Main idea:
Let's simulate the above algorithm for every suffix and record the obtained answer in $$$ans_i$$$ for $$$i^{th}$$$ suffix. Note that the value $$$ans_i$$$ doesn't denote any answer for some suffix because the sum of $$$b_i$$$ over that suffix might or might not be zero. One important observation here is that-
- Let some subarray $$$a[l:r]$$$ for which sum of $$$b_i$$$ is $$$0$$$, then $$$ans_l - ans_{r+1}$$$ do have a good meaning, it's the answer for that query indeed.
Our answer for $$$a[l:r]$$$ would have been the result of simulation on the subarray, but how does simulation on $$$l^{th}$$$ suffix looks?
It greedily matches the subarray $$$a[l:r]$$$ first because the sum of $$$b_i$$$ is zero, so it will surely pair up all elements in that subarray. Then it moves further on $$$r+1$$$ and continuing the simulation after $$$r+1$$$ is equivalent to starting the simulation from $$$r+1$$$ itself because $$$psum$$$ so far (defined above) would be automatically 0.
Note that $$$ans_l$$$ doesn't have any physical meaning because it will add some junk value if elements after $$$r+1$$$ are not paired up equally but those junk values are exactly same in $$$ans_l$$$ and $$$ans_r$$$ which cancel out, giving the correct answer.
But still, we can't simulate for every suffix, right? It would go $$$O(n^2)$$$ again.
Let's iterate from left to right and for every $$$i$$$ try calculating it's contribution in $$$1^{st}$$$, $$$2^{nd}$$$, ..., $$$(i-1)^{th}$$$ suffixes which is easy because it depends only on $$$psum_i$$$, $$$b_i$$$ (which are constant for a given $$$i$$$) and $$$psum_l$$$ for contribution to $$$l^{th}$$$ suffix. This is pretty standard using $$$2$$$ fenwick trees.
How to calculate $$$ans_i$$$?
Let's solve $$$b_i \gt 0$$$ and $$$b_i \lt 0$$$ independently, say $$$b_i \gt 0$$$ for now. Other case is similar.
Let $$$psum_i = \sum_{j=1}^{i}b_j$$$.
Consider the contribution of index $$$i$$$ to $$$ans_l$$$ for $$$l \lt i$$$, from three cases described above the contribution is different for different $$$l$$$ with different $$$psum_l$$$. We can build a fenwick tree on compressed prefix sums. Case $$$1$$$ and $$$2$$$ above add a constant value to a range of prefix sums that can be maintained in one fenwick tree and Case $$$2$$$ gives some linear function of $$$psum$$$ to be added in a range that can be maintained in other fenwick tree. Add contribution of each $$$i$$$ from $$$1$$$ to $$$n$$$ first, and let's start calculating $$$ans_i$$$.
For $$$i = 1$$$, $$$ans_1$$$ can be obtained by querying at $$$psum_1$$$ in both fenwicks.
Then we remove the contribution of $$$i = 1$$$ from the two fenwick trees (simply the negative of which we added above), because $$$i = 1$$$ won't be contributing to any suffix other than $$$1^{st}$$$ one.
Similarly we move from left to right and calculate $$$ans_i$$$ by querying at $$$psum_i$$$ and then remove the contribution of $$$i^{th}$$$ element.
#include<bits/stdc++.h>
using namespace std ;
#define ll long long
#define pb push_back
#define all(v) v.begin(),v.end()
#define sz(a) (ll)a.size()
#define F first
#define S second
#define INF 2000000000000000000
#define popcount(x) __builtin_popcountll(x)
#define pll pair<ll,ll>
#define pii pair<int,int>
#define ld long double
template<typename T, typename U> static inline void amin(T &x, U y){ if(y<x) x=y; }
template<typename T, typename U> static inline void amax(T &x, U y){ if(x<y) x=y; }
#ifdef LOCAL
#define debug(...) debug_out(#__VA_ARGS__, __VA_ARGS__)
#else
#define debug(...) 2401
#endif
const int MOD=1000000007;
struct Mint {
int val;
Mint(long long v = 0) {
if (v < 0)
v = v % MOD + MOD;
if (v >= MOD)
v %= MOD;
val = v;
}
static int mod_inv(int a, int m = MOD) {
int g = m, r = a, x = 0, y = 1;
while (r != 0) {
int q = g / r;
g %= r; swap(g, r);
x -= q * y; swap(x, y);
}
return x < 0 ? x + m : x;
}
explicit operator int() const {
return val;
}
Mint& operator+=(const Mint &other) {
val += other.val;
if (val >= MOD) val -= MOD;
return *this;
}
Mint& operator-=(const Mint &other) {
val -= other.val;
if (val < 0) val += MOD;
return *this;
}
static unsigned fast_mod(uint64_t x, unsigned m = MOD) {
#if !defined(_WIN32) || defined(_WIN64)
return x % m;
#endif
unsigned x_high = x >> 32, x_low = (unsigned) x;
unsigned quot, rem;
asm("divl %4\n"
: "=a" (quot), "=d" (rem)
: "d" (x_high), "a" (x_low), "r" (m));
return rem;
}
Mint& operator*=(const Mint &other) {
val = fast_mod((uint64_t) val * other.val);
return *this;
}
Mint& operator/=(const Mint &other) {
return *this *= other.inv();
}
friend Mint operator+(const Mint &a, const Mint &b) { return Mint(a) += b; }
friend Mint operator-(const Mint &a, const Mint &b) { return Mint(a) -= b; }
friend Mint operator*(const Mint &a, const Mint &b) { return Mint(a) *= b; }
friend Mint operator/(const Mint &a, const Mint &b) { return Mint(a) /= b; }
Mint& operator++() {
val = val == MOD - 1 ? 0 : val + 1;
return *this;
}
Mint& operator--() {
val = val == 0 ? MOD - 1 : val - 1;
return *this;
}
Mint operator++(int32_t) { Mint before = *this; ++*this; return before; }
Mint operator--(int32_t) { Mint before = *this; --*this; return before; }
Mint operator-() const {
return val == 0 ? 0 : MOD - val;
}
bool operator==(const Mint &other) const { return val == other.val; }
bool operator!=(const Mint &other) const { return val != other.val; }
Mint inv() const {
return mod_inv(val);
}
Mint power(long long p) const {
assert(p >= 0);
Mint a = *this, result = 1;
while (p > 0) {
if (p & 1)
result *= a;
a *= a;
p >>= 1;
}
return result;
}
friend ostream& operator << (ostream &stream, const Mint &m) {
return stream << m.val;
}
friend istream& operator >> (istream &stream, Mint &m) {
return stream>>m.val;
}
};
template<typename T=long long>
struct fenwick {
vector<T> bit;
int n;
fenwick(int x) {
n = x;
bit.resize(x + 1, T(0));
}
void update(int j,T val)
{
for(;j<=n;j+=j&-j)
bit[j] += val;
}
T get(int r)
{
T u = 0;
for(;r;r-=r&-r)
u += bit[r];
return u;
}
T query(int l,int r)
{
return get(r)-get(l-1);
}
// kth element
int getKth(T k) {
int ans = 0;
T cnt = 0;
for(int i=20;i>=0;--i) {
if(ans + (1 << i) <= n && cnt + bit[ans + (1 << i)] < k) {
ans += (1 << i);
cnt += bit[ans];
}
}
if(ans == n) {
return -1;
}
return ans + 1;
}
void insert(int x) {
update(x, 1);
}
void erase(int x) {
update(x, -1);
}
};
int _runtimeTerror_()
{
int n;
int Q;
cin >> n >> Q;
vector<array<int,2>> a(n);
for(int i=0;i<n;++i) {
cin >> a[i][0];
}
for(int i=0;i<n;++i) {
cin >> a[i][1];
}
vector<Mint> val(n, 0);
for(int i=n-1;i>=0;--i) {
if(i < n - 1) {
val[i] = val[i + 1];
}
val[i] += a[i][0] * Mint(abs(a[i][1]));
}
auto solve = [&](vector<array<int,2>> &a) {
ll psum = 0;
vector<ll> psums;
psums.push_back(0);
for(int i=0;i<n;++i) {
psum += a[i][1];
assert(a[i][1] != 0);
psums.push_back(psum);
}
sort(all(psums));
psums.resize(unique(all(psums)) - psums.begin());
psum = 0;
auto get_next = [&](ll x) {
return lower_bound(all(psums), x) - psums.begin() + 1;
};
fenwick<Mint> f1(2*n), f2(2*n), f3(2*n);
for(int i=0;i<n;++i) {
if(a[i][1] > 0) {
f1.update(1, Mint(a[i][1]) * a[i][0]);
f1.update(get_next(psum), -Mint(a[i][1]) * a[i][0]);
f2.update(get_next(psum), a[i][0]);
f2.update(get_next(psum + a[i][1]), -a[i][0]);
f3.update(get_next(psum), Mint(a[i][0]) * Mint(psum + a[i][1]));
f3.update(get_next(psum + a[i][1]), -Mint(a[i][0]) * (psum + a[i][1]));
}
psum += a[i][1];
}
psum = 0;
for(int i=0;i<n;++i) {
val[i] -= 2 * f1.get(get_next(psum));
val[i] -= 2 * (f3.get(get_next(psum)) - psum * f2.get(get_next(psum)));
if(a[i][1] > 0) {
f1.update(1, -Mint(a[i][1]) * a[i][0]);
f1.update(get_next(psum), Mint(a[i][1]) * a[i][0]);
f2.update(get_next(psum), -a[i][0]);
f2.update(get_next(psum + a[i][1]), a[i][0]);
f3.update(get_next(psum), -Mint(a[i][0]) * Mint(psum + a[i][1]));
f3.update(get_next(psum + a[i][1]), Mint(a[i][0]) * (psum + a[i][1]));
}
psum += a[i][1];
}
};
solve(a);
for(int i=0;i<n;++i) {
a[i][1] = -a[i][1];
}
solve(a);
val.push_back(0);
while(Q--) {
int l, r;
cin >> l >> r;
--l, --r;
cout << val[l] - val[r + 1] << "\n";
}
return 0;
}
int main()
{
ios_base::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#ifdef runSieve
sieve();
#endif
#ifdef NCR
initialize();
#endif
int TESTS = 1;
//cin >> TESTS;
while(TESTS--)
_runtimeTerror_();
return 0;
}
Hello Codeforces!
I'm Jatin, a member of COPS IIT(BHU). I attempted a screen-cast of Codeforces Round #747 (DIV. 2) followed by a short discussion of the solutions to problems. I managed to solve the first 6 problems (A — E2) and got 242 overall rank.
Video:Screencast
Do subscribe to our channel and share the content if you find it helpful. As always, feel free to comment below.
Thanks for reading and see you in the next contest!
Hi Everyone !! I am Jatin Garg from Competitive Programming Group IIT BHU. Today I attempted to make the screencast In Hindi for the Codeforces Round 697 (Div3). I was able to solve all problems during the contest and got 144th rank. I also shared my approach to solving the problems during the contest.
Do check it out:
— https://www.youtube.com/watch?v=Ha3Xw9Tq1Po
Do like and subscribe to the channel. We will be posting editorials for future contests, so stay tuned.
Hi Everyone !! I am Jatin Garg from Competitive Programming Group IIT BHU. Yesterday I attempted to make the screencast for the Codeforces Round 693 (Div3). I was able to solve problem A to E and G during the contest (got 330th rank) and later upsolved F in a separate video. I also shared my approach to solve the problems during the contest.
Do check it out:
— https://www.youtube.com/watch?v=Wzz5psk5PWs (Screencast)
— https://www.youtube.com/watch?v=x4oIUhKpsk8 (Problem F)
Do like and subscribe to the channel. We will be posting editorials for future contests, so stay tuned.
| Name |
|---|










