651A - Joysticks
Idea author: fcspartakm, preparation: fcspartakm.
Main idea is that each second we need to charge the joystick with lowest power level. We can just emulate it or get an O(1) formula, because process is very simple.
651B - Beautiful Paintings
Idea author: fcspartakm, preparation: fcspartakm.
Lets look at the optimal answer. It will contain several segment of increasing beauty and between them there will be drops in the beautifulness. Solution is greedy. Lets sort all paintings and lets select which of them will be in the first increasing segment. We just go from left to right and select only one painting from each group of several paintings with the fixed beauty value. We continue this operation while there is at least one painting left.
With the careful implementation we will get  solution.
solution.
But this solution gives us the whole sequence, but the problem was a little bit easier — to determine number of such segments. From the way we construct answer it is easy to see that the number of segments always equal to the maximal number of copies of one value. Obviously we can't get less segments than that and our algorithm gives us exactly this number. This solution is O(n).
651C - Watchmen/650A - Watchmen
Idea author: ipavlov, preparation: ipavlov.
When Manhattan distance equals to Euclidean distance?
deu2 = (x1 - x2)2 + (y1 - y2)2
dmh2 = (|x1 - x2| + |y1 - y2|)2 = (x1 - x2)2 + 2|x1 - x2||y1 - y2| + (y1 - y2)2
So it is true only when x1 = x2 or y1 = y2. This means that to count the number of such pair we need to calculate number of points on each horizontal line and each vertical line. We can do that easily with the use of std::map/TreeMap/HashMap/Dictionary, or just by sorting all coordinates.
If we have k points on one horizontal or vertical line they will add k(k - 1) / 2 pairs to the result. But if we have several points in one place we will count their pairs twice, so we need to subtract from answer number of pairs of identical points which we can calculate with the same formula and using the same method of finding equal values as before.
If we use TreeMap/sort then solution will run in  and if unordered_map/HashMap then in O(n).
and if unordered_map/HashMap then in O(n).
651D - Image Preview/650B - Image Preview
Idea author: fcspartakm, preparation: fcspartakm.
What photos we will see in the end? Some number from the beginning of the gallery and some from the end. There are 4 cases:
- We always go right.
- We always go left.
- We initially go right, then reverse direction, go through all visited photos and continue going left.
- We initially go left, then reverse direction, go through all visited photos and continue going right.
First two cases are straightforward, we can just emulate them. Third and fourth cases can be done with the method of two pointers. Note that if we see one more picture to the right, we spend more time on the right side and the number of photos seen to the left will decrease.
This solution will run in O(n).
Alternative solution is to fix how many photos we've seen to the right and search how many we can see to the left with binary search. For this method we will need to precompute times of seeing k pictures to the right and to the left. But this is solution is  , which is slightly worse then previous one, but maybe it is easier for somebody.
, which is slightly worse then previous one, but maybe it is easier for somebody.
651E - Table Compression/650C - Table Compression
Idea author: LHiC, preparation: iskhakovt.
First we will solve our problem when all values are different. We will construct a graph, where vertices are cells (i, j) and there is an edge between two of them if we know that one is strictly less then the other and this relation should be preserved. This graph obviously has no cycles, so we can calculate answer as dynamic programming on the vertices:
for ( (u, v) : Edges) {
dp[v] = max(dp[v], dp[u] + 1);
}
We can do this with topological sort or with lazy computations.
But if we will construct our graph naively then it will contain O(nm(n + m)) edges. To reduce this number we will sort each row and column and add edges only between neighbours in the sorted order. Now we have O(nm) edges and we compute them in 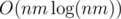 time.
time.
But to solve the problem completely in the beginning we need to compress all equal values which are in the same rows and columns. We can construct second graph with edges between equal cells in the same way as before and find all connected components in it. They will be our new vertices for the first graph.
650D - Zip-line
Idea author: LHiC, preparation: LHiC.
We need to find the longest increasing subsequence (LIS) after each change if all changes are independent.
First lets calculate LIS for the initial array and denote its length as k. While calculating it we will store some additional information: lenl[i] — maximal length of LIS ending on this element. Also we will need lenr[i] — maximal length of LIS starting from this element (we can calc it when searching longest decreasing sequence on reversed array).
Lets solve the case when we take our new element in the resulting LIS. Then we just calculate maxi < a, h[i] < b(lenl[i]) + 1 + maxj > a, h[j] > b(lenr[j]). It can be done online with persistent segment tree or offline with scanline with regular segment tree in  time. This is the only case when answer can be larger then k, and it can be only k + 1 to be exact. Second case is when we change our element and ruin all LIS of size k. Then answer is k - 1. Otherwise we will have at least one not ruined LIS of size k and it is the answer.
time. This is the only case when answer can be larger then k, and it can be only k + 1 to be exact. Second case is when we change our element and ruin all LIS of size k. Then answer is k - 1. Otherwise we will have at least one not ruined LIS of size k and it is the answer.
Lets calculate number of different LIS by some modulo. It can be done with the same dynamic programming with segment tree as just finding LIS. Then we can check if liscount = liscountleft[a] * liscountright[a]. This exactly means that all sequences go through our element.
But if you don't want the solution with such "hashing" there is another approach. For each element we can calc if it can be in LIS. If so then we know on which position it will go (lenl[i]). Then for each position we will know if there are several elements wanting to go on that position or only one. If only one then it means that all LIS are going through that element.
Overall complexity is  .
.
P.S. We can solve this without segment tree, just using alternative approach to calculating LIS with dynamic programming and binary search.
650E - Clockwork Bomb
Idea author: Zlobober, preparation: Zlobober.
First idea is that answer is always equals to the number of edges from the first tree, which are not in the second one. This means that if we have an edge in both trees we will never touch it. So if we have such edge we can remove this edge and merge its two vertices together, nothing will change.
Second idea that if we will take any edge from the first tree there always exists some edge from the second tree, which we can swap (otherwise second graph is not connected, but the tree is always connected). So the order of adding edges from the first tree can be arbitrary.
Third idea is that if we will select leaf node in the first tree, then cut its only edge, then we can add instead of it any edge going from this vertex in the second tree.
Overall algorithm: we store linked lists of edges in vertices, when edge is in both trees we use disjoint-set union to merge vertices and join their lists. We can simply traverse first tree to get any order of edges in which the current edge will always contain leaf as one of its vertices.
Complexity is O(nα), which in practice is almost linear.








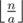 . Otherwise we need to buy glass bottles while we can. So, if we have at least
. Otherwise we need to buy glass bottles while we can. So, if we have at least 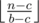 glass bottles and then spend rest of the money on plastic ones. This is simple
glass bottles and then spend rest of the money on plastic ones. This is simple 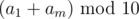 from the rightmost digit of the sum. Lets figure out what does
from the rightmost digit of the sum. Lets figure out what does 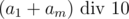 equals to. If the remainder is 9, it means that
equals to. If the remainder is 9, it means that 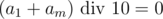 , because we can't get 19 out of the sum of two digits. Otherwise the result is defined uniquely by the fact that there was carrying 1 in the leftmost digit of the result or not. So after this we know
, because we can't get 19 out of the sum of two digits. Otherwise the result is defined uniquely by the fact that there was carrying 1 in the leftmost digit of the result or not. So after this we know 
