651A - Джойстики

Автор идеи: fcspartakm, разработчик: fcspartakm.

Главной идеей решения является то, что в каждый момент времени нам нужно заряжать джойстик с самым низким уровнем заряда. По-этому мы можем просто проэмулировать процесс или вывести простую формулу за O(1).

651B - Красота картин

Автор идеи: fcspartakm, разработчик: fcspartakm.

Давайте посмотрим на ответ, в нем будет несколько подряд идущих отрезков возрастания красоты, а между ними красота будет падать. Будем решать задачу жадно: давайте отсортируем массив значений и будем набирать возрастающие куски по очереди. Чтобы набрать очередной кусок мы идем слева-направо и среди каждого множества картин с одинаковым значением мы выберем только одно. Так будем продолжать пока картины не закончатся.

Если аккуратно это реализовать, то получим решение за .

Но такое решение дает нам всю последовательность, но в задаче от нас по-сути просили вычислить только число отрезков возрастания. Из прошлого решения следует, что мы наберем столько отрезков возрастания, сколько максимум раз повторяется в массиве одно из наших чисел. Очевидно, что мы не можем набрать меньше. Получаем решение за O(n).

651C - Хранители/650A - Хранители

Автор идеи: ipavlov, разработчик: ipavlov.

Когда манхетенское расстояние совпадает с евклидовым?

d_eu² = (x₁ - x₂)² + (y₁ - y₂)²

d_mh² = (|x₁ - x₂| + |y₁ - y₂|)² = (x₁ - x₂)² + 2|x₁ - x₂||y₁ - y₂| + (y₁ - y₂)²

Это означает, что они равны только когда x₁ = x₂ или y₁ = y₂. Что посчитать ответ нам нужно выяснить, сколько точек лежат на каждой горизонтальной и на каждой вертикальной прямой. Это легко сделать с помощью std::map/TreeMap/HashMap/Dictionary, или если просто отсортировать координаты.

Если у нас есть k точек на одной горизонтальной или вертикальной прямой, то они добавят в ответ k(k - 1) / 2 пар. Но таким образом мы дважды посчитаем пары совпадающих точек, то есть нужно будет вычесть из ответа посчитанные таким же способом числа пар одинаковых точек.

Если мы воспользовались TreeMap/sort, то мы получим решение за , а если unordered_map/HashMap, то O(n).

651D - Просмотр фотографий/650B - Просмотр фотографий

Автор идеи: fcspartakm, разработчик: fcspartakm.

Какие фотографии мы увидим в конце? Сколько-то от начала и возможно сколько-то с конца. Всего есть 4 случая:

• Мы всегда двигались только вправо.
• Мы всегда двигались только налево.
• Сначала мы двигались направо, потом сменили направление движения, прошли все просмотренные фото и продолжили движение налево.
• Сначала мы двигались налево, потом сменили направление движения, прошли все просмотренные фото и продолжили движение направо.

Первые два случая делаются банально, просто эмулируем. Третий и четвертый случай можно решить с помощью метода двух указателей. Заметим, что если мы пройдем в третем случае на одну картину больше справа, то мы потратим больше времени и число просмотренных фото слева уменьшится. Так двигаем эти два указателя и пересчитываем текущее время.

Это решение работает за O(n).

Альтернативным решением является зафиксировать сколько мы пройдем справа, а потом найти сколько мы пройдем слева с помощью бинарного поиска. Для этого нам нужно будет предподсчитать для каждой позиции слева и справа, сколько времени мы потратим, дойдя до нее.

Это работает за , что немного дольше, но возможно кому-то так проще было решать.

651E - Сжатие таблицы/650C - Сжатие таблицы

Автор идеи: LHiC, разработчик: iskhakovt.

Сначала решим задачу, когда все значения различны. Мы построим граф, где вершинами будут являться ячейки таблицы, а ребра будут вести из одной ячейки в другую, если у первой значение меньше, чем у второй и они лежат в одной строке или в одном столбце. В этом графе нет циклов, так что мы можем вычислить сжатые номера ответа с помощью динамического программирования:

for ( (u, v) : Edges) {
	dp[v] = max(dp[v], dp[u] + 1);
}

Мы можем это сделать с помощью топологической сортировки или ленивых вычислений.

Если мы построим граф как описано, то в нем будет O(nm(n + m)) ребер. Чтобы уменьшить это число мы отсортируем каждую строку и каждый столбец и добавим ребра только между соседями в этом порядке. Тепеть у нас O(nm) ребер, которые мы вычисляем за время .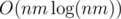

Теперь вспомним про одинаковые значения. Давайте построим точно так же второй граф, но теперь в нем ребра будут означать равенство. Теперь если мы найдем компоненты связности в этом графе, они и будут являться вершинами нашего нового первого графа.

650D - Канатная дорога

Автор идеи: LHiC, разработчик: LHiC.

Нам нужно вычислять длину наибольшей возрастающей подпоследовательности (НВП) после каждого из независимых изменений к массиву.

Для начала вычислим длину НВП в нашем исходном массиве и обозначим её за k. Пока мы это вычисляем, нам понадобится хранить дополнительную информацию len_l[i] — максимальную длину НВП, заканчивающуюся на данном элементе. Аналогично нам понадобится len_r[i] — максимальная длина НВП, начинающейся с данного элемента (мы можем это вычислить аналогично, только нужно будет идти по массиву в обратную сторону).

Давайте решим тот случай, когда наш новый элемент будет лежать в новой НВП. Длина максимальной НВП, проходящей через эту точку будет равна max_{i < a, h[i] < b}(len_l[i]) + 1 + max_{j > a, h[j] > b}(len_r[j]). Это можно вычислить онлайн с помощью персистентного дерева отрезков или оффлайн с помощью обычного дерева отрезков и метода сканирующей прямой, что будет работать за на запрос. Это единственный случай, когда ответ будет больше k, точнее он может быть только k + 1.

Во втором случае, когда наш элемент не входит в ответ, но то что мы его поменяли привело к порче всех исходных НВП, то ответ будет k - 1. Иначе у нас останется хотя бы одна НВП длины k, она и будет ответом.

Как это понять? Давайте посчитаем число НВП в исходном массиве по какому-нибудь модулю. Мы можем это сделать с помощью динамического программирования также, как мы искали саму НВП, например с помощью дерева отрезков. Тогда мы можем проверить, если liscount = liscount_left[a] * liscount_right[a], то это как раз означает, что все НВП проходят через наш элемент.

Если вам не нравится решение с таким "хешированием", то есть алтернативный честный подход. Для каждого элемента давайте поймем, может ли он входить в какую-нибудь исходную НВП, а если может, то на какой позиции(эта позиция будет как раз равна len_l[i]). Тогда для каждой позиции мы посчитаем, сколько различных элементов претендуют на нее. Если только один элемент, то это как раз и означает, что все НВП проходят через него.

Получаем решение за .

P.S. Мы можем решить эту задачу без использования структур данных с помощью альтернативного метода вычисления НВП с помощью динамического программирования и бинарного поиска.

650E - Часовой механизм

Автор идеи: Zlobober, разработчик: Zlobober.

Первое соображение: ответ всегда равен числу ребер, которые есть в первом дереве, но которых нет во втором. Это означает, что если у нас есть ребро, которое лежит в обоих деревьях, то это ребро можно удалить, а те две вершины, которые оно соединяло, объединить в одну, ничего не изменится.

Второе соображение: если мы возьмем любое ребро из первого дерева и удалим его, то всегда найдется корректное ребро из второго дерева, которое можно вставить обратно (если такого нету, то это означает, что второй граф не связен, а он дерево, противоречие). Таким образом порядок замены ребер из первого дерева может быть произвольный.

Третье соображение: если мы взяли лист в первом дереве, выкинули соответствующее ему ребро, то мы можем добавить любое ребро из второго дерева, которое ведет из данной вершины.

В итоге получаем алгоритм: храним списки ребер в вершинах, когда ребро общее, то объединяем вершины с помощью системы непересекающихся множеств, а их списки склеиваем вместе. Чтобы получить порядок ребер в первом дереве мы сделаем его обход в глубину и получим такой список, что если мы уже убрали все прошлые ребра, то следующее всегда будет листом.

Получаем асимптотику O(nα), что на практике является линейным алгоритмом.

625A - Гость из прошлого

Автор идеи: народное творчество, разработка: feldsherov.

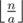Заметим, что если у нас больше либо равно b денег, то суммарная стоймость стеклянной бутылки составляет b - c копеек. Значит если a ≤ b - c, то нам не имеет смысла покупать стеклянные бутылки и ответ будет . Иначе выгоднее в начале покупать стеклянные бутылки, пока можно. В этом случае, если у нас есть хотя бы 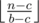b денег, мы купим стеклянных бутылок, а на остаток докупим пластиковых. Получаем решение формулами за O(1).

625B - Война корпораций

Автор идеи: gustokashin, разработка: thefacetakt.

Давайте для начала найдем первое вхождение второго слова в первое. Так как нам нужно запретить первое вхождение, то куда бы нам поставить решетку внутри этого слова? Понятно, что в самую правую позицию, чтобы запретить как можно больше вариантов вхождений данного слова. После этого давайте надем следующее вхождение после поставленной решетки и повторим операцию. Самая простая реализация работает за O(|S|·|T|), но с помощью продвинутых алгоритмов поиска подстроки в строке (например, алгоритм Кнута-Морриса-Пратта) можно добиться асимптотики O(|S| + |T|).

Hint/Bug/Feature: в языке Python уже реализована функция, которая делает ровно то, что описано в условии:

print(input().count(input()))

625C - K-специальные таблички

Автор идеи: Андреева Елена Владимировна, разработка: wilwell.

Давайте заполнять строки таблицы по очереди жадным образом. Мы хотим, чтобы на k-м месте стояло максимальное число. В этой строке после него должно быть n - k значений, строго больших него, то есть наше число будет не больше n² - (n - k). Давайте все эти числа и поставим в первой строке после k-го столбца. А на первые k - 1 мест давайте ставить минимальные числа, то есть 1,  2,  ... ,  k - 1. В следующей строке давайте поступим абсолютно таким же образом, тогда в начале будут идти числа от k до 2(k - 1), а начиная с k-го будут идти следующие максимально возможные числа, то есть от n² - (n - k) - (n - k + 1) до n² - (n - k + 1). Таким образом мы заполним всю таблицу. Заметим, что при эффективной реализации нам не нужно хранить саму таблицу, можно обойтись O(1) памяти. Сам алгоритм работает за размер ответа, то есть O(n²).

625D - Контрольная по арифметике

Автор идеи: Sender, разработка: Sender.

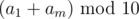Если длина суммы равна n, то длина иходного числа равна n, если не было переноса, либо n - 1, если был перенос. Зафиксируем длину и обозначим ее за m. Обозначим i-ю цифру искомого числа за a_i. Тогда заметим, что мы знаем . Попробуем понять чему равно 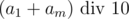. Если остаток равен 9, то так как максимальная сумма двух цифр равна 18, значит 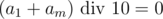. В противном случае результат однозначно определяется тем, был ли перенос в самом левом разряде при сложении или нет. Получается, что мы выяснили чему равно a₁ + a_m. Заметим, что абсолютно неважно, как мы распределим эту сумму между первым и последним разрядом — сумма чисел не поменяется. Зная эти разряды мы можем определить, был ли перенос в сложении после первого разряда и до последнего. Повторяя эту операцию m / 2 раз мы сможем восстановить всё требуемое число. Получаем итоговую асимптотику O(n).

Если не заметить однозначности перехода, то можно реализовать данное решение с помощью динамического программирования.

625E - Лягушачьи бои

Автор идеи: Андреева Елена Владимировна, разработка: iskhakovt.

Давайте аккуратно моделировать процесс. Заведем структуру данных, в которой будем хранить все ключевые события, которые могут произойти с лягушками (кто-то ест кого-то). Тогда мы можем доставать из нашей структуры событие, которое произойдет раньше всех, выполнять прыжок и пересчитывать изменившиеся события. В качестве структуры можно воспользоваться стандартной структурой set языка C++ или TreeSet языка Java или рукописным деревом отрезков. Для того, чтобы быстро понимать, кого следующего будет есть наша лягушка, будем хранить их в двусвязном списке в порядке обхода нашего поля. Тогда мы легко сможем понимать, кого мы пытаемся есть впереди и кто пытается съесть нас. Техническим нюансом является вычислить по двум лягушкам ближайший момент времени, когда первая съест вторую, но это легко делается из физических соображений линейного движения двух точек. Так как лягушек может умереть не более n - 1, то весь алгоритм в итоге будет работать за .

1. tourist
2. PavelKunyavskiy
3. -XraY-
4. Monyura
5. Sfairat
6. qwerty787788
7. KADR
8. izban
9. I-juice
10. maksay
11. Dmitry_Egorov
12. Nerevar
13. Milanin
14. slavik
15. Igor_Kudryashov
16. tomasz.kociumaka
17. jablko
18. Arterm
19. TeaPot
20. Fefer_Ivan
21. mexmans
22. Bobik
23. Rubanenko
24. zeliboba
25. Shtrix
26. vlad107
27. Copymaster
28. Fdg
29. Kostroma
30. Um_nik
31. romanandreev

А футболки дают первым 20...

Если кого пропустил — пишите, добавлю.

Будем решать задачу динамикой, но для начала нам нужно понять несколько вещей:

1) Каждый подотрезкок длины M отличается от следующего не белее чем в одной позиции тогда и только тогда, когда выполнены 2 условия:

a) Разрежем наш абажур ПОСЛЕ серой лампочки, и дальше разобьем его на R = N/M кусков длины M. Тогда прошлое условие точно должно выполняться для каждого из наших R отрезков.

b) Пусть для лампочки с номером x выполняется color[x] != color[(x + m) % n] и аналогичное условие для y != x. Тогда расстояние между x и y >= m.

(Доказательство почти тривиально=) )

2) Нарисуем такую матрицу M x R, где a[i][j] будет 1, если color[i + j * M] != color[(i + j * M — m) % n]. (столбцы нумеруются слева-направо, строки снизу вверх) В каждом столбце будет не более 1 единички(это по условию a). Тогда из условия b следует, что 1 будут идти слева направо и снизу вверх(график неубывает), потом пустой столбец(возможно несколько), и опять неубывающая последовательность, итп.

3) Рассмотрим строчку с номером m — 1. Она соответствует серой лампочке и следующим после нее на расстоянии кратном m. В ней в начале должно стоять несколько единиц, то есть в начале такая горизонтальная линия идет.

4) В остальных строчках либо пусто, либо есть F единиц. Сколько способов это покрасить, чтобы в конце мы опять вернулись в нужный нам цвет? Это легко считается простейшей динамикой D[F][last_color], можно ее и значительно быстрее считать, но нам это не нужно=)

А теперь начинается самое интересное — динамика для ответа=)

Зафиксируем число пустых столбцов P.

Будем идти по строкам снизу вверх и хранить то, сколько нам нужно поставить еще 1 в эту матрицу. Понятно, что нам надо поставить R — 1 — P единиц(мы не рассматриваем 1 столбец, для него все и так получится хорошо, ведь мы в 4 пункте так специальную дп считали).

dp[rows][ones]

Чтобы ее почитать, переберем сколько 1 мы ставим в эту строку. А дальше через несложные C из n по k понимаем, сколько способов расставить наши 1 в те возрастающие последовательности между P пустыми строки.

Также тут возникает 2 случая, соответственно из пункта 3 и 4.

Ну и нам остается просуммировать по всем P соответствующие dp[M][R — 1 — P].

Вот=)

PS Возможно я где-то накосячил с понятием верх-низ или с +-1, но я думаю суть понятна.

PPS Мы сдали эту задачу в дорешивание, на контесте мы пытались динамику из 4 пункта считать тоже какой-то формулой, но как-то сходу не получилось, и в общем недодебагали, обидно...

Я пытаюсь сдать задачу 118A - Упражнение на строки, но получаю вердикт "Отказ тестирования", причем при разных посылках одного и того же кода, этот вердикт проявляется на разных тестах, что-то тут не так=)

1243513

Причем это так не только у меня, но и у других пользователей, например у blozo.