Usual questions:
- What is the scoring distribution?
- Is there interactive problem?
- Will there be thanks to MikeMirzayanov for the best systems Codeforces and Polygon?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Usual questions:
We cordially invite the Codeforces community to participate in the 5th ProgNova Programming Contest, which will take place next Friday, February 7, 5-8pm EST. The contest will be hosted online on Kattis and feature an original problemset.
Problems have been prepared and tested by yubowenok, szfck, zapray, Sotskin, zpl1, MRain, and saketh. The contest will be harder than a typical ICPC North American regional, but easier than a typical ICPC World Finals. We hope this will in particular provide a good warmup opportunity for contestants competing in the 2020 ICPC North America Championship. The problem-set is designed to offer something to all levels of competitive programmers.
All students enrolled in North American universities are welcome to participate in the North America Division and compete for prizes. All others are welcome to join the Open Division and win raffles. Prizes are sponsored by BlindData.
Registration via the contest website is required and must be completed by Wednesday, February 5, 11:59pm EST. Participation is individual.
If you have any questions, feel free to ask me or email [email protected].
We look forward to seeing you at the contest!!
Here is a modular segment tree implementation with range query and lazy range update. I have borrowed heavily from Al.Cash's segment tree post a few months ago, so first, a big thanks to him!
You can find the code here. The main feature is that it takes template arguments to specify its behavior:
template<typename T, typename U> struct seg_tree_lazy
so that it is usable without any modification to the pre-written code. Instead, it takes a type T for vertex values, and a type U for update operations. Type T should have an operator + specifying how to combine vertices. Type U should have an operator () specifying how to apply updates to vertices, and an operator + for combining two updates.
As an example, let's see how to use it to support the follow operations:
The T struct would look like this:
struct node {
int sum, width;
node operator+(const node &n) {
return { sum + n.sum, width + n.width };
}
};
And the U struct would look like this:
struct update {
bool type; // 0 for add, 1 for reset
int value;
node operator()(const node &n) {
if (type) return { n.width * value, n.width };
else return { n.sum + n.width * value, n.width };
}
update operator+(const update &u) {
if (u.type) return u;
return { type, value + u.value };
}
};
Additionally, the constructor takes a value T zero, the "zero" node, and a U noop, the "zero" update. If these are not provided, the default constructors for T and U are used. For this particular use case we would write:
seg_tree_lazy<node, update> st(N, {0, 0}, {false, 0});
Then, we set the leaf values:
vector<node> leaves(N, {0, 1});
st.set_leaves(leaves);
And we're done! With this example we can see the power of modularization; the amount of code we had to touch is very small. You can see the full implementation with I/O here if you want to play with it.
Finally, here are some other usage examples:
Let me know if you have any suggestions!
In this problem we are given a directed graph, and asked whether a particular vertex is reachable from vertex 1. It is possible to solve this by running a depth-first search starting from vertex 1.
Since every vertex has at most one outgoing edge, it is possible to write the DFS as a simple loop. Some people used this to make very short submissions.
Imagine a graph with one vertex for each entry in the permutation, and edges between pairs of swappable entries. It is easy to see that no matter how many swaps we make, no entry can end up in a location that is not in its connected component. We can also show that within any connected component, we can achieve any rearrangement of the entries that we wish.
Since we want to make the lexicographically smallest permutation, we should greedily rearrange the entries within each connected component so that they are in increasing order.
N ≤ 300, so we are not concerned with runtime. One can determine the connected components using a number of standard algorithms (Floyd-Warshall, Union Find, etc.).
Consider an arbitrary day d, on which we must read book b. Let d' be the last day before d on which book b was read (if there is no previous day, let d' = - ∞). Observe that, on day d, we cannot avoid lifting all of the books read on any day between d' and d. If we add up all the weights of these required liftings, we will have a lower bound on the answer.
This lower bound can be computed with two loops, in O(M2) time. We must be sure not to add a book's weight multiple times, if it was read multiple times in the interval (d', d).
If we initially arrange the books in order of the first day on which they are read, we will achieve the described lower bound. So, we have our answer.
By linearity of expectation, E(d(c1, c2) + d(c1, c3) + d(c2, c3)) = E(d(c1, c2)) + E(d(c1, c3)) + E(d(c2, c3)). By symmetry, those three values are all equal. So, we need only compute E(d(c1, c2)). We can multiply it by 3 to find the answer.
Let us imagine that a random selection (c1, c2, c3) is made. We'll define a function f(j), for each edge j, so that f(j) = wj if j is part of the shortest path from c1 to c2, and f(j) = 0 otherwise. Observe that 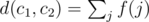 . Again by linearity, we have
. Again by linearity, we have 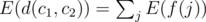 .
.
We can write E(f(j)) = wj·P(j), where P(j) is the probability that edge j is included in the path from c1 to c2. If we compute P(j) for all j, we can then compute 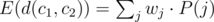 in O(N). Also, we can handle updates in O(1); if wj changes to w'j, we subtract wj·P(j) from the answer, and add w'j·P(j).
in O(N). Also, we can handle updates in O(1); if wj changes to w'j, we subtract wj·P(j) from the answer, and add w'j·P(j).
So, let's figure out P(j) for each j. Any edge j, if removed from the tree, separates the graph into two separate connected components a and b. Edge j will be included in the shortest path from c1 to c2 if and only if one of them is in a, and the other is in b. So, we want the number of ways to select (c1, c2, c3) such that c1 and c2 are on opposite sides of edge j, divided by the total number of ways to select (c1, c2, c3). Let's have |a| and |b| denote the number of vertices in a and b, respectively. Then 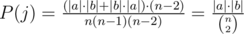 .
.
To figure out |a| and |b| for each j, we can root the tree arbitrarily and compute the depth and subtree size for each vertex in O(N) time. Then for an edge j, if vj is the deeper vertex incident to j, we know one component has size equal to the subtree size of vj. For the other component, we use the fact that |b| = N - |a|.
When domino i is knocked over, it covers the interval [pi, pi + li]. If we see a query (xj, yj), it is equivalent to the question "If we knock over all dominoes with index 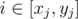 , how much of the interval [pxj, pyj] won't be covered?" We can modify that question a little more, to say that we knock over all dominoes with index i ≥ xj, without changing its answer.
, how much of the interval [pxj, pyj] won't be covered?" We can modify that question a little more, to say that we knock over all dominoes with index i ≥ xj, without changing its answer.
Now, consider knocking over the dominoes from right to left. As soon as we knock over domino i, we will immediately process all of the queries with xj = i, and record their answers. What we need is a data structure that supports two operations: "cover range [pi, pi + li]" (when we knock over a domino) and "compute how much of the range [pxj, pyj] is not covered" (when we wish to answer a query). This can be done using coordinate compression and a segment tree.
It's worth noting there are a lot of other ways to solve this problem. The other tutorial uses a completely different approach. Also, the approach described here may be implemented using different data structures. For example, here is my implementation using BBSTs and a Binary Indexed Tree.
We will use the standard dynamic programming approach for 0/1 knapsack. To summarize what it does for us, imagine we are given an ordered list of items (ci, hi). Let F(k, b) be the maximum happiness we can buy, if we consider only the first k items in the list, and have a budget of b. If K is the size of the list, and B is the maximum possible budget, we can compute F(k, b) for all possible k and b in O(KB) time.
Let us sort all of the items by their display time. Suppose that we focus on the queries (aj, bj) with 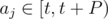 , for some particular t. Let A be a list of the items with display time in (t - P, t], and let B be a list of the items with display time in (t, t + P). Let both lists be sorted in order of display time.
, for some particular t. Let A be a list of the items with display time in (t - P, t], and let B be a list of the items with display time in (t, t + P). Let both lists be sorted in order of display time.
Every query with 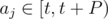 will have available to it some suffix of A, along with some prefix of B. We'll do a knapsack DP on the elements of A, in reverse order, and another on the elements of B, in normal order. Finally, to answer any query (aj, bj) with
will have available to it some suffix of A, along with some prefix of B. We'll do a knapsack DP on the elements of A, in reverse order, and another on the elements of B, in normal order. Finally, to answer any query (aj, bj) with 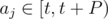 , we can consider all possible ways to split the budget bj between the items in A and the items in B, in linear time. For each possible way to split the budget, we need simply look up one value from each DP table to know the maximum possible happiness.
, we can consider all possible ways to split the budget bj between the items in A and the items in B, in linear time. For each possible way to split the budget, we need simply look up one value from each DP table to know the maximum possible happiness.
If we perform the process above on t = 1, 1 + P, 1 + 2P, 1 + 3P, ... until t exceeds the maximum possible day D, we'll be able to answer all of the queries. Let's think about the runtime of this solution. For each t, the described process takes O(KB) time, where K is the number of items whose display time is in (t - P, t + P). Each object can only appear in up to two of these intervals. So, the overall runtime for all of the knapsack DP's we perform is O(nB). Computing the final answer takes O(B) per query, or O(qB) overall.
Don't know how to solve this yet. Maybe someone who is not gray can provide the solution. :)
| Name |
|---|


