The Following Introduction to The Fenwick Tree is Intended to be Easy to Understand and Targeted At Newbies , any Suggestion to make it Easier Will be Appreciated I was Introduced to Competitive Programming a Few weeks Ago Precisely Three and One of the First Data Structures i Encountered Was The Fenwick Tree, Its one of The Most Easy to Implement Form of Binary Indexed Trees out There and greatly Helps in Solving Problems With Deal With Statistical Cumulative Frequency of a Class , NOTE : Here Class Represents Statistical Interval Range And Not OOP Concept Firstly Some of The Basic Concepts Relating To Cumulative Frequency : Lets Say I Have to Add Marbles to a Particular Box (From a Range of Boxes ) and Then Report The Query of The Following Type From The Data :

• The Total Number of Marbles
• The Total Number of Marbles From Box U to V;
• Marbles in Box U

Lets Say I Have the Following Data For Four Marble Boxes

Serial Number of Box	Number of Marbles in the box
1	3
2	5
3	3
4	2
5	3
6	2

Lets First See How we Would Report The Following Queries From The Above Arrangement of Data :

• Report The Total Number of Marbles :
  1.) Take a variable Total
  2.) Go Through each Box And Then Add The Number of Marbles of it to Total
  3.) Report The Total Number of MarblesI Don't Think i Need to Tell You This But This Process Has the Time Complexity in Order of Θ( N ) And Has a Space Complexity of  Θ( N+1 )For If you have 2 Boxes It Would be Okay , But That's Never the Case in Competitive Programming is it ? in your Way Through You are Going to Have to Deal With Sample Input Ranging From Mere 10 To 10^8  To A Massive  >10^18 ( You need Special Techniques to handle These As They Cannot Be Accommodated into A Single Array) And Therefore Here This Arrangement of Data Falls Short .
• Total Number of Marbles From U to V :
  1.) Start Iterating From U and Keep Track of Number of marbles
  2.) Go Till V
  3.) Report The Total Again This is Also Linear Time And Takes in Order of Θ(V-U+1), And Like Said Earlier This Can Cross The Time Limit Very Easily and You Might Encounter The Most Dreaded TLE .
• Reporting Marble in U Takes Constant Time Θ(1)

In Basic Statistics you might Recall From 8th Grade That We Use Cumulative Frequencies to Operate on Data Now Let's Use The Cumulative Frequency Table

Serial Number of Box	Number of Marbles in the box	Cumulative Frequency
1	3	3
2	5	8 (5+3)
3	3	11 (8+3)
4	2	13 (11+2)
5	3	16 (13+3)
6	2	18 (16+2)

Cumulative Frequency of i th Class is Defined as The Total Sum of The Frequency of The i th Class With The Cumulative Frequency of The i-1 th Class , With The First Class Having the Cumulative Frequency Equal to its Frequency Now Let's See How we Would Handle Queries on the Basis of The Above Arrangement:

• Report The Total Number of Marbles Θ(log n)  Read The Cumulative Frequency of Nth Element
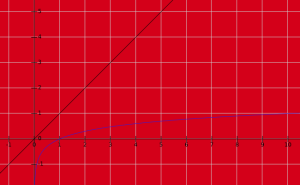
• Report The Number of Marbles Between The Range U and V Read The Cumulative Frequency of  V th Element  Minus U-1 th Element  Θ(Time Taken to Read) in a Fenwick Tree it Takes in Order of A Mere Θ(2* log n), Which By A Large Margin a Way Less Than What we Had Before. Look at The graphic

  Black Line — N
  Blue — Log N

As you Would've Seen From The Graphic Θ(log n) will Pass Tight Constraints , Whereas Simple Arrangement Won't And So For Problems That Involve Queries over a Range , We use Fenwick Trees For Prefix Sums . Idea or Intuition Behind Fenwick Trees : What we Do is We Take The Least Significant Digit  From a Number's binary Representation For N  by                      Expression N&-N And Use it To Iterate Through The Array , Now This Iteration Depends on Pattern of The Binary Number and Use it as a Map For Iterating Through Array By Adding it to The Index to Move Forward              and Subtracting to Iterate Back. Here is a Textbook Definition From Various Sources :

• The basic rule that the structure works on is that, just like a number can be represented as a sum of some powers of two, so can a cumulative sum be represented as a sum of some partial cumulative sums . (Algorithmist)

Suppose we are looking for cumulative frequency of index 13 (for the first 13 elements). In binary notation, 13 is equal to 1101. Accordingly, we will calculate c[1101] = tree[1101] + tree[1100] + tree1000{Note How on every successive iteration one 1 bit is removed from the sequence , That's the magic of n&-n , try solving it by your hand , Note -n refers to two's complement } Here is a Table of Responsibility , That is It Shows How One Could Iterate Through the Array From The Binary Representation of a Particular Index

Let's First See how n&-n Works ,

1. let N = 13
2. The Binary Representation of N is 1101
3. The One's Complement of N is 0010 (NOT Operation,Flipping of Digits) + 1 ,
4. Therefore Two's Complement of N should be
   !(1101)+1 = 0010 + 1 = 0011;
5. Consider the Two's Complement Representation to be M=0011
6. Taking N & M (AND operation) we get
   1101
   &0011
   _____
   0001
7. In a Read Operation We subtract it from N&M from N ,
   which Leads to 1101(13) — 0001(1) = 1100 , Which Gives the Next Index For The Array Element
8. Similarly For 1100, Two's Complement is 0011+1= 0100, And Thu 1100-0100 = 1000
   
9. Note That in case of 1000 Two's Complement is 0111+1 = 1000 , Which Leads to Next N being 1000-1000=0000 ,And Here the Binary Tree Indexed by Digits of 13 Ends, Therefore The Cumulative Frequency of 13 is Stored in 1101,1100 and 1000 ,
10. Binary Indexed Tree is the clever way of storing cumulative frequencies on the basis of the sequence of numbers formed in the process of removal of the Least Significant Digit From The Binary Representation of a number . Similarly when we update 1000(8), the value gets updated in 1000,1100 and 1101, Try doing it by hand but this time add N&-M to N .

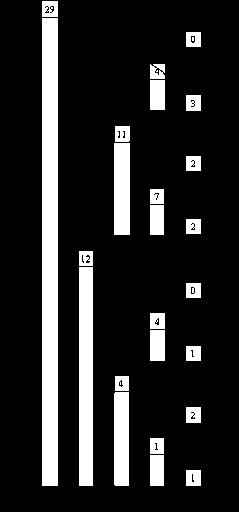
From Topcoder , NOTE :- Perfect Powers of 2 like 1 ,2 ,4 ,8 ,16 . Store The Cumulative Frequency From the Start , unlike Other Indexes Which are Dis-Continuous , Wonder Why ? Write Down the Binary Representation of Powers of 2 and Then Start Removing The Least Significant Digit (1) One by one , and I am Sure you'll Figure it Out

Note The Reason 0 Doesn't Link to Other Index is Because 0&-0 is Zero , That is Fenwick Tree only Works on One Indexed Arrays Now The Idea Behind BIT is That we Initialize an Array Of Size  The Serial Number of Classes + 1 (Relative For Negative Indexes and Discontinuous Sets) What we Do is Initially we  Initialize all The Elements a Value of Zero and Use a Function Update to Represent Change in  Cumulative Frequency, Basically We Represent The Cumulative frequency By The Change With Each Input Query , and Update The Value . What we Do is We First Take The Index n and Then extract the Least Significant Digit one  and Iterate Forward Till we are Lesser Than The MAXIMUM Length of The Array

 typedef long long int ll; //lazy kid , Guilty ! 
void update( ll n, ll val) { 
for(;n<=MAXVAL;arr[n]+val,n+=n&-n); // Add The Value in The Index and Move Forward according to //The Binary Pattern 
}

Similarly For Reading The Cumulative Frequency of a Particular Class , we Iterate In backward Direction By Subtracting N&-N From the Index N

ll read(ll n) { 
ll sum=0; for(;n;sum+=arr[n],n-=n&-n); 
return sum;
}

Finding the Frequency in a Range U and V Takes a Function Call

return read(V)-read(U-1);

And Similarly For Reading The Frequency For a Position There Exists a Faster Method Here , Otherwise One Can Replace U and V with The Same Index with The Previous Function Call. The Operation Takes  2 * Θ( log n)

Reducing Space Complexity and Optimizing With Relative Mapping :

Now That Would be all For Implementing The Simple Fenwick Tree However One Might Further optimize it And Help reduce Space Complexity and Length of The Original Array ,By Relatively Mapping It For Example Consider we Have a Set of Values for a Class Defined By S = {1 , 2, 3 ,4 ,10^5} now for representing a Set of Only 5 Elements  we would have to Create an Array With Length 10^5 + 1, And Trust me Not So Good , Rather Than That WE Could Reduce The Space Complexity From Ω( Magnitude of Largest Element +1 ) to Ω(Size of Distinct Elements),

PS: —  and how The Hell Would You Create a Normal BIT For This S = {0, -2, -3 ,-4 ,-10^5,-10^2} For That We Use The Following Algorithm For Number of Classes N , and Two arrays (Vectors)   a ,  And Binary Indexed Tree b is

map( N, a, b) temp; a.clear(); //resize array to 0 b.clear(); //resize array to 0 FOR i = 0 to n: INPUT temp push temp to End of a push temp to End of b

sort( b ) //sort b 
          FOR i = 0 to N 
           replace the i th element with the Position of The First Occurrence of the i th element in Sorted Array B +1 
            resize b to size of N+ 1

Here is a Code to Implement The Above Mapping

typedef long long int ll;
using namespace std;
void update(ll n, ll val, vector &b);
ll read(ll n,vector &b);
ll readsingle(ll n,vector &b);
void map(vector &a,vector &b,ll n) /**** RElative Mapping ***/
{
    ll temp;
    a.clear();
    b.clear();
    for(ll i=0; i<n; i++)
    {
        scanf("%lld",&temp);
        a.push_back(temp);
        b.push_back(temp);
    }
    sort(b.begin(),b.end());
    for(ll i=0; i<n; i++)
        *(a.begin()+i) = (lower_bound(b.begin(),b.end(),a[i])-b.begin())+1;
    b.assign(n+1,0);
}
ll readsingle(ll n,vector &b)
{
    return read(n,b)-read(n-1,b);
}
ll read(ll n,vector &b)
{
    ll sum=0;
    for(; n; sum+=b[n],n-=n&-n);
    return sum;
}
void update(ll n, ll val, vector &b)
{
    for(; n<=b.size(); b[n]+=val,n+=n&-n);
}

Hope it Helped :) , Will Post one on Two Dimensional as Soon as i Learn it :) Thanks For Reading , Any Suggestions Mention or Mistakes Them Below