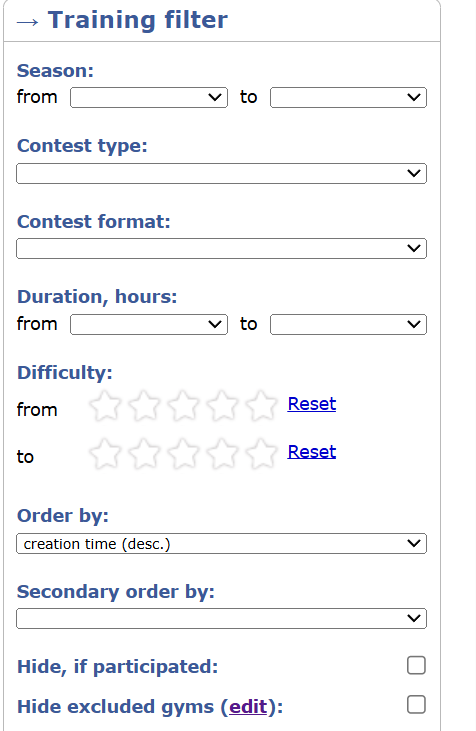
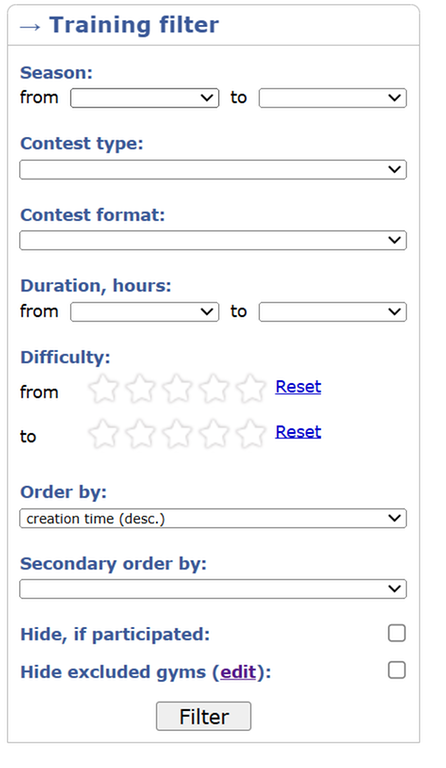
In the contests interface, I can filter those contests that I have already attempted, but there is no such feature in gyms. What should I do in this case? Is there any method for that?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |


In the contests interface, I can filter those contests that I have already attempted, but there is no such feature in gyms. What should I do in this case? Is there any method for that?
2018-2019 ACM-ICPC, China Multi-Provincial Collegiate Programming Contest
We define $$$A$$$ is the permutation of n, and $$$B$$$ is a sequence of n.
$$$B_i$$$ is defined as the number of subscripts that satisfy the condition
Obviously,after a round of bubbling,$$$B_i$$$will minus one (if $$$B_i>0$$$), and $$$A_i$$$ will also move forward one space (i--)(although this is useless).
We consider to use sequence $$$B$$$ to solve the problem, we first prove that for every valid sequence $$$B$$$, there is exactly one permutation $$$A$$$ corresponding to it.
We consider how to infer $$$A$$$ from $$$B$$$.
It is very obvious that $$$A_n$$$ (the length of the permutation is n) can be directly infered by $$$B_n$$$, and $$$A_{n-1}$$$ is also easily to know if $$$A_n$$$ is known,and so on. So as long as $$$B$$$ is legal, there is an $$$A$$$ permutation obtained, certificated.
That is to say, for each bubbling, every $$$B_i$$$ greater than $$$0$$$ is decremented by one, and equal to $$$0$$$, it remains unchanged.
The transformation of $$$B$$$ is easy to stimulate by the conclusion (Obviously,...).
So we only need to calculate the legal number of sequence of $$$B$$$.
Consider what final states are legal:
All $$$B_i=0$$$ (ie $$$A$$$ is ordered)
There is a consecutive subsequence of $$$B_i=1$$$ in the permutation, and the rest are 0, such as 0 0 1 1 0 (1 4 2 3 5)
There is only one $$$B_i!=0$$$ in the permutation, and the others are 0, such as 0 0 2 0 0 (2 3 1 4 5)
I think it is easy to use Dynamic programming to solve this problem, set 3 states is ok.
memset(dp,0,sizeof(dp));
int ans2=0;
cin>>n>>m>>mod;
dp[0][0]=1;
for(int i=1;i<=n;i++){
if(i<=m+1){
(dp[i][0]+=dp[i-1][0]*(i))%=mod;
}
else{
(dp[i][0]+=dp[i-1][0]*(m+1))%=mod;
(dp[i][1]+=dp[i-1][0]+dp[i-1][1])%=mod;
(dp[i][2]+=dp[i-1][1]*(m+1)+dp[i-1][2]*(m+1)+dp[i-1][0]*max(0ll,i-1-(m+1)))%=mod;
}
}
int ans=0;
for(int i=0;i<3;i++)ans+=dp[n][i];
cout<<"Case #"<<ts<<": "<<ans%mod<<"\n";
| Name |
|---|


