I was recently solving some problems on Linearity of Expectation. I was trying to solve the Coupon collector problem. The problem is: Given n coupons, how many coupons do you expect you need to draw with replacement before having drawn each coupon at least once? This is how I tried to solve the problem:
E[Number of coupons needed to draw so that each coupon comes atleast once]
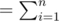 E[Number of coupons drawn till i'th coupon is drawn for the first time]
E[Number of coupons drawn till i'th coupon is drawn for the first time]
This comes from the Linearity of Expectation (Link) since independency or dependency of events does not matter.
Now, let E[Number of coupons drawn till i'th coupon is drawn for the first time] = x
This can be solved by applying the following recursive equation,
x = 1 + ((n - 1) / n) * x
On solving, we get x = n.
Thus, E[Number of coupons needed to draw so that each coupon comes atleast once] = n2
I know that I am wrong somewhere since the answer is n * Hn, but I don't know where exactly does it go wrong. I have discussed this with my friend kr_abhinav, but we couldn't find the mistake in the proof as well.









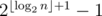 . The problem can be solved by locating each element in the list and checking whether it is
. The problem can be solved by locating each element in the list and checking whether it is  .
. 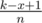 .
.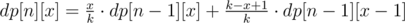
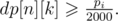
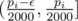 passes the system tests.
passes the system tests.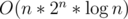 . This will not be accepted. We can use the following optimizations for this problem:
. This will not be accepted. We can use the following optimizations for this problem: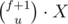
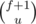 is the number of ways of choosing
is the number of ways of choosing 

